Рассмотрим пример решения трансцендентного (т. е. содержащего неалгебраические функции) уравнения:
(2x3 + 3)(1 – sin(x)) = ln(x) + 2.
Пусть начальное приближение к решению равно 1.
Рассмотрим вариант оформления данной задачи:
1) выделите ячейки A1:D1 и нажмите кнопку Объединитьи поместитьв центрена панели инструментов Форматирование. Введите надпись «Решение уравнения»;
2) выделите ячейки A2:D2 и
нажмите кнопку Объединить и поместить в центрена
панели инструментов Форматирование. Введите надпись
«(2x3 + 3)(1 –
sin(x)) = ln(x) + 2»;
3) в ячейку В4 введите начальное приближение 1;
4) задайте имя ячейке В4. Для этого выделите ячейку и выполните команду Вставка, Имя, Присвоить;
5) в ячейку С4 введите левую часть преобразованного уравнения, перенеся все его элементы в одну часть: «=(2*x^3 + 3)*(1 - sin(x)) – ln(x) – 2»;
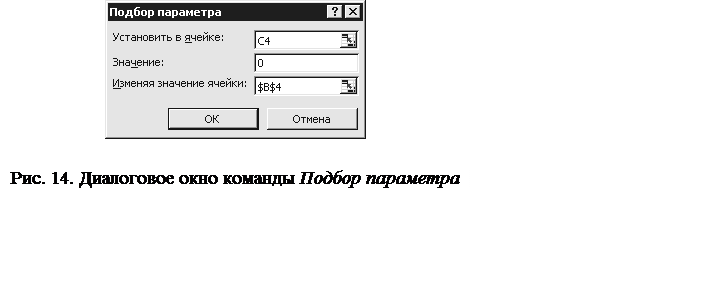
6) задайте в диалоговом окне команды Подбор параметра значения, указанные на рис. 14;
7) нажмите кнопку ОК;
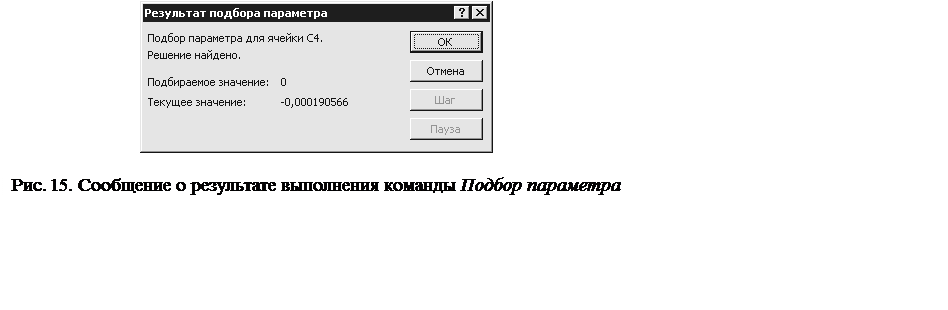
8) появится окно с сообщением о результате решения (см. рис. 15);
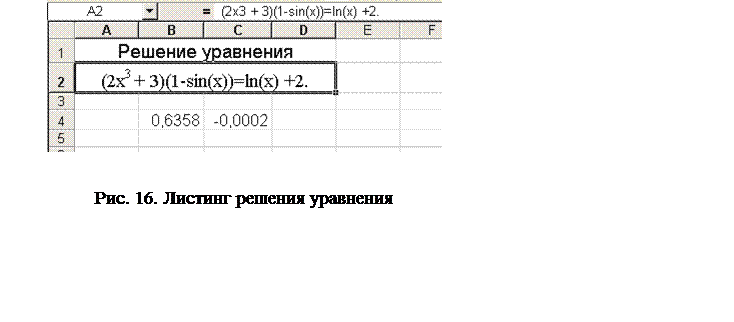
9) нажмите кнопку ОК. Электронная таблица примет вид, изображенный на рис. 16.
Если решение не устраивает, можно его повторить, задав новое начальное приближение, точность вычисления и предельное число итераций.
 |
 |
||
9.5. Поиск решения
Команда Подборпараметрапозволяет найти подходящее значение одной переменной. Обычно решение формулы зависит от большего числа переменных. Кроме того, часто требуется найти не конкретное числовое значение, а оптимальное решение, удовлетворяющее ряду дополнительных условий на значения используемых параметров. Для решения таких задач в Excel используется н а д с т р о й к а(т. е. специальное средство, расширяющее возможности Excel) Поискрешения. Если Excel был установлен в полной конфигурации, то меню Сервиссодержит команду Поискрешения. Иначе нужно выбрать команду Сервис, Надстройки, в списке надстроек указать Поискрешения и нажать ОК. После этого Excel спросит, нужно ли добавить этот компонент, на что следует ответить утвердительно.
В основе надстройки также лежат итерационные методы, но ее возможности гораздо больше, нежели у команды Подборпараметра. Надстройка Поискрешенияпозволяет
использовать одновременно большое количество изменяемых ячеек;
задавать ограничения для изменяемых ячеек;
получать не заранее известный результат в какой-либо ячейке, а найти оптимальное (минимальное или максимальное), т. е. наилучшее из возможных, решение;
для сложных задач генерировать множество различных решений и сохранять эти решения (с этим вопросом можно ознакомиться по справке Excel).
Целевая ячейка, в которой формируется нужный результат, единственная.
Рассмотрим некоторые примеры.
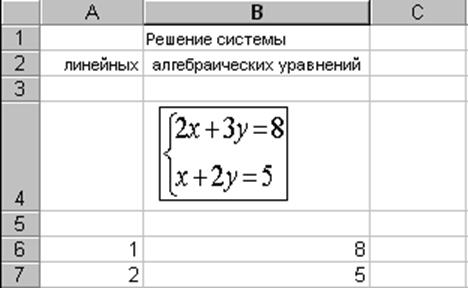
Решим систему линейных алгебраических уравнений (СЛАУ) 2-го порядка:
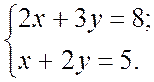 |
1) в первых двух строчках электронной таблицы запишите формулировку задачи;
2) увеличьте ширину четвертой строки;
3) с помощью редактора формул наберите систему уравнений;
4) в ячейки А6 и А7 введите произвольные начальные значения х и у. В данном примере выбраны нулевые значения;
5) в ячейку В6 введите формулу «=2*А6 + 3*А7», в В7 – «= А6 + 2*А7». Экран в режиме отображения формул приобретет вид, изображенный на рис. 17;
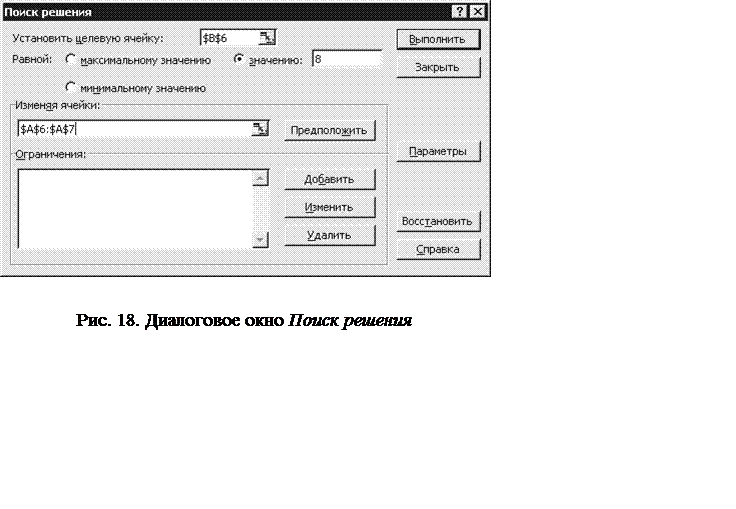
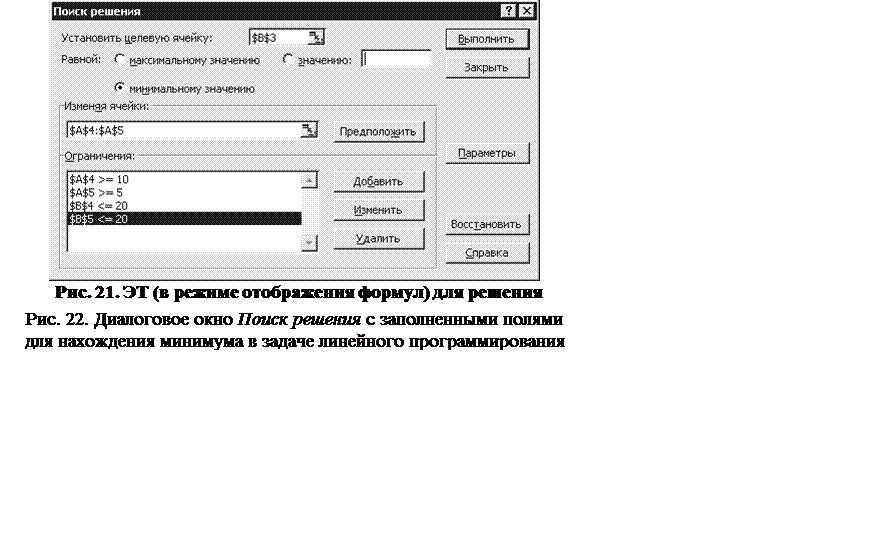
6) выполните команду Сервис, Поиск решения. Появится диалоговое окно этой команды (рис. 18). В поле Установить целевую ячейкувведите $B$6, в поле Равнойзначению– число 8, в поле Изменяяячейки – $A$6:$A$7;
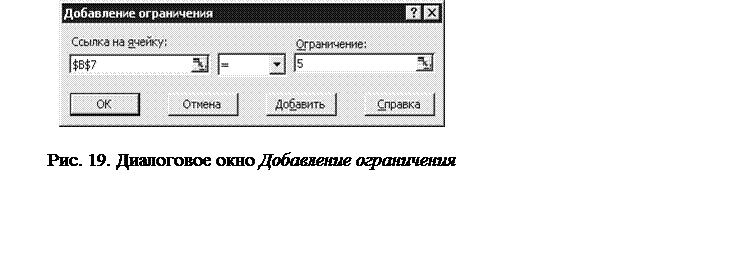
7) используйте второе уравнение системы в качестве ограничения. Для этого нажмите кнопку Добавитьдиалогового окна Поискрешения. Появится диалоговое окно Добавлениеограничения (рис. 19). Заполните его поля;
8) нажмите клавишу ОК. Вернется диалоговое окно Поискрешения, в поле Ограничениякоторогобудет запись «$B$7=5». Нажмите кнопку Выполнить. В появившемся диалоговом окне Результатыпоискарешениявыберите Сохранитьнайденноерешениеи нажмите ОК. Результат решения приведен на рис. 20.
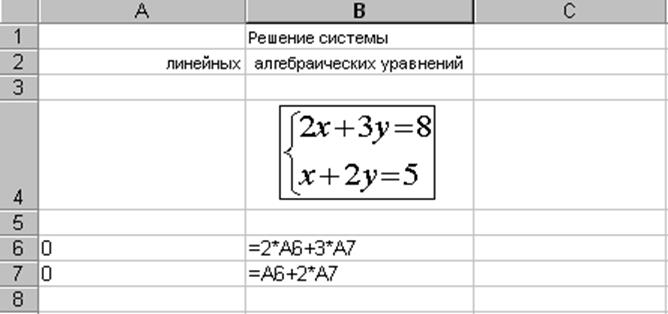 |
Рис. 17. Решение СЛАУ (режим отображения формул)
 |
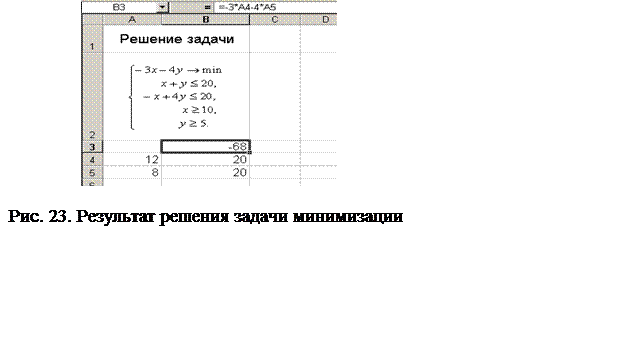
В качестве другого примера рассмотрим задачу: найти минимальное значение функции z = – 3x – 4y, если ограничения на значения х и y заданы системой:
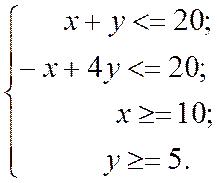
Эта задача относится к задачам линейного программирования. Она легко может быть решена в Excel. ЭТ (электронная таблица) с исходными данными для решения этой задачи (режим отображения формул) показана на рис. 21. Начальные значения х и у (ячейки А4 и А5) выбраны произвольно. Как надо заполнить поля диалогового окна Поиск решения, показано на рис. 22. Результат вычислений: ЭТ в режиме отображения значений приведена на рис. 23.
З а м е ч а н и е. Решение задачи линейного программирования будет найдено быстрее, если в диалоговом окне Поискрешения нажать кнопку Параметрыи установить флажок Линейнаямодель.
 |
9.6. Понятие о макросах
Если при работе с Excel часто приходится выполнять одну и ту же последовательность действий, то ее можно записать и дать ей имя. Такая записанная под определенным именем последовательность называется макросом. Для записей макросов используется язык программирования Microsoft Visual Basic. Макросы можно использовать не только при работе в Excel, но и при работе в Word. В обоих приложениях существует возможность автоматической записи макроса без программирования на языке Visual Basic, которая будет рассмотрена в данных методических указаниях.
задачи минимизации
 |
Макросы можно запускать на выполнение различными способами.
В данных методических указаниях будут рассмотрены только два способа.
Ставшие ненужными макросы можно удалять.
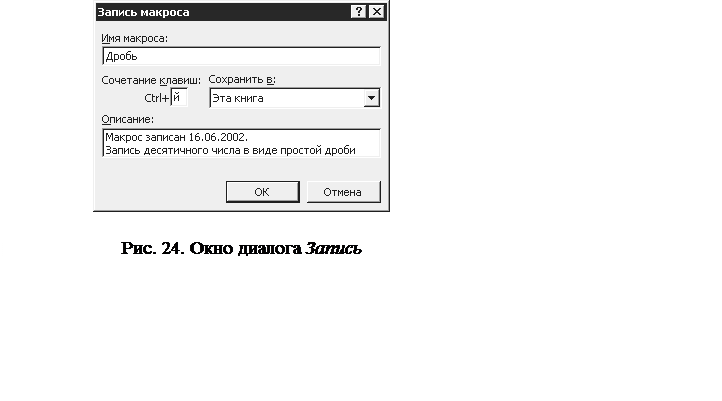
Рассмотрим п р и м е р. Пусть при работе с некоторой рабочей книгой часто используется дробный формат с двумя цифрами. Это означает, что дробные значения выводятся на экран как обычные, а не как десятичные дроби. При этом в числителе и знаменателе находится одна или две цифры. Запишем макрос Число. Для этого выполните следующие действия:
1) выберите команду Сервис, Макрос, Начать запись. Excel выведет на экран окно диалога Записьмакроса (рис. 24);
2) назначьте имя макросу;
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.