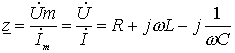Исследование двухполюсников в цепи синусоидального тока, страница 5

,

где элементов R, L, С в комплексной форме;

5. Комплексная проводимость цепи:

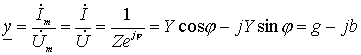
Следует обратить внимание на знак «-» перед реактивной проводимостью.

6. Комплексное сопротивление последовательного соединения участков:

7. Комплексная проводимость параллельного соединения участков:

8. Комплексное сопротивление участков с комплексными сопротивлениями  и  соединенных параллельно:

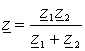
Содержание п.п.3-8 позволяет заключить, что определение комплексных сопротивлений и проводимостей, а также комплексных действующих значений (амплитуд) токов и напряжений формально то же, что и при расчете простых цепей постоянного тока. Следовательно, пользуясь перечисленными комплексными величинами, можно выполнять расчет токов и напряжений исследуемой простой цепи, пользуясь всеми приемами, известными из теории цепей постоянного тока. Заключительным этапом такого расчета будет переход от найденных комплексных амплитуд или действующих значений токов и напряжений к соответствующим синусоидальным функциям.

Векторная диаграмма на комплексной плоскости, как следует из рис.1, 2, строится по комплексным числам, выражающим токи и напряжения. Пример построений по числовым данным показан в приложении на рис.10,а, 12.

Топографическая диаграмма-это особое взаимное расположение векторов на векторной диаграмме, которое будет широко использоваться в одном из последующих основных разделов курса, но с которым необходимо познакомиться первоначально на примере простой цепи.

Физический смысл топографической диаграммы состоит в следующем. Если потенциал одной из точек цепи принять равным нулю, то потенциалы остальных точек, изменяющиеся по закону синуса, могут быть представлены векторами. Последние, в свою очередь, могут быть получены с помощью векторов падений напряжения на участках цепи. Итак, понятие топографическая диаграмма относится только к векторам напряжений, векторы токов могут быть нанесены на нее как вспомогательные.