Исследование двухполюсников в цепи синусоидального тока, страница 2

Известно, что ряд задач по расчету цепей может быть решен с помощью векторных диаграмм. Геометрические операции над векторами просты и наглядны, но они недостаточно точны. Этот недостаток может быть исключен, если векторы и соответствующие им синусоидальные функции представлять комплексными числами. В таком случае геометрические операции заменяются алгебраическими операциями.

Любое комплексное число А может быть представлено в трех формах:

 - алгебраическая форма;

 - тригонометрическая форма;

 - показательная форма.

Каждому комплексному числу соответствует на комплексной (гауссовой) плоскости, (рис.1) вполне определенная и единственная точка, а, следовательно, и единственный вектор, проведенный из начала координат в эту точку.

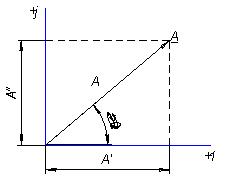
Рис. 1. Комплексное число на комплексной плоскости

Для перехода от одной формы записи комплексного числа к другим формам используются следующие соотношения:

,(1)

,(2)

,(3)

,(4)

.(формула Эйлера).

В приведенных выражениях е - основания натуральных логарифмов; ; А - модуль комплексного числа; А’ и A”  - вещественная и мнимая чести комплексного числа; a - аргумент комплексного числа;  - оператор поворота вектора на угол a. В электротехнике, как показано на рис.1, принято располагать ось +j сдвинутой на 90° от оси +1 в направлении против вращения стрелки часов. В том же направлении отсчитываются от оси +1 положительные значения угла a.