Исследование двухполюсников в цепи синусоидального тока, страница 3

Пользуясь соотношениями (1)-(4), нетрудно получить следующие равенства:

, , , .

Следует иметь в виду, что  в формуле (4) не определяет угол a однозначно. Угол уточняется сопоставлением знака  со знаками , или .

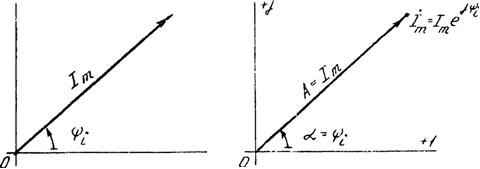
Рис. 2. Вектор на комплексной плоскости

В основах теории переменных токов для представления синусоидальных функций использовались неподвижные или вращающиеся с угловой скоростью векторы в декартовой плоскости. Для перехода к комплексной плоскости (рис.2), в соответствии с изложенным выше, ось вещественных должна быть направлена по оси абсцисс, а ось мнимых - по оси ординат. Тогда в комплексной плоскости неподвижный вектор, изображающий, например, синусоидальный ток, есть комплексное число с модулем, равным амплитуде синусоидальной функции, и аргументом, равным ее начальной фазе, т.е.. Такое комплексное число носит название комплексной амплитуды тока.

Как в аналитическом, так и в комплексном методе, наибольший практический интерес представляют величины в  раз меньшие амплитуд. Комплексные величины (5) называют соответственно комплексными действующими значениями тока и напряжения:

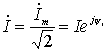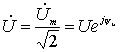,   (5)

Следует обратить внимание, что допускается для обозначения комплексных амплитудных и действующих значений величин, являющихся синусоидальными функциями времени, взамен способов, указанных выше, над основным обозначением ставить точку. Именно такое обозначение и распространено в электротехнике.