Исследование двухполюсников в цепи синусоидального тока, страница 4

Вращающемуся вектору на комплексной плоскости соответствует комплексное число с постоянным модулем и переменным аргументом, например (для вектора, изображающего синусоидальное напряжение). Такое комплексное чисто называют символическим изображением синусоидальной функции или ее комплексным мгновенным значением. Представим его в алгебраической форме (6):

.(6)

Получаем: синусоидальная функция (в некоторых учебниках ее при этом называют оригиналом) может быть определена как мнимая часть ее символического изображения, взятая без j,

В целях сокращения записи рассмотренных соотношений используется знак Û, который читается "соответствует" или "изображает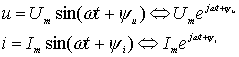" (7):

(7)

Знак Û может быть поставлен также между комплексной амплитудой и синусоидальной функцией (8);

(8)

Ниже приводятся основные формулы, применяемые при расчете цепей синусоидального тока комплексным методом и подробно излагаемые в лекционной части курса.

1. Символическое изображение производной синусоидальной функции:

2. Символическое изображение интеграла синусоидальной функции (с учетом того, что постоянная интегрирования равна нулю):

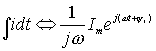
3. Контурное уравнение для последовательного соединения приемников R , L, С , подключенного к источнику синусоидального напряжения u . Закон Ома в комплексной форме:

Это же уравнение в комплексной форме:

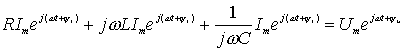
После сокращения на :

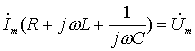
4. Комплексное сопротивление цепи: