Спектр нормальных колебаний решетки, распределение колебаний по частотам. Понятие о фононах

Тема 4.1.  Спектр нормальных колебаний решетки, распределение колебаний по частотам. Понятие о фононах.

Вопрос 10

Понятие о фононах

Процессы, происходящие в твердых телах, связанные с колебаниями атомов кристаллической решетки, выглядят особенно просто, если обратиться к одному из самых фундаментальных обобщений квантовой механики. В основе этого обобщения лежит идея де Бройля о том, что каждую волну с частотой  ω и  волновым вектором К можно сопоставить с частицей с энергией  и импульсом . Аналогично квантам электромагнитных волн, называемых фотонами, вводят понятие кванта упругой волны – фонона. Почти все концепции, используемые в применении к фотонам, например концепция корпускулярно-волнового дуализма, в равной степени хорошо подходят и к фононам. Звуковые волны в кристаллах можно рассматривать как распространение фононов. Тепловые колебания атомов в кристаллах можно рассматривать как термическое возбуждение фононов.

Ранее мы обсуждали методы получения информации о структуре кристалла, которую можно получить при упругом (брэгговском) рассеянии нейтронов, электронов и рентгеновского излучения на кристаллической решетке.

Неупругое рассеяние медленных нейтронов является одним из основных методов изучения колебаний решетки. Нейтроны испытывают неупругое рассеяние при взаимодействии с кристаллами, в результате чего энергия и импульс изменяются таким образом, что эти изменения соответствуют возникновению или поглощению одного или более фононов. Точное измерение эффектов, связанных с такими процессами, позволяет определить свойства отдельных фононов и в частности установить зависимость частоты от волнового вектора, т. е. закон дисперсии.

Фонон с волновым вектором К взаимодействует с другими частицами или полями так, как если бы он имел импульс . В действительности фонон в решетке не имеет импульса (только фонон с волновым вектором К = 0 имеет физически существующий импульс). Величину  для фонона называют квазиимпульсом. Использование понятия квазиимпульс не означает, что через кристалл передастся «обычный» импульс с соответствующей скоростью; однако квазиимпульс — это величина, которая сохраняется в различных процессах взаимодействия, включающих в себя рождение и уничтожение фононов. Поэтому торможение нейтрона при возбуждении в решетке колебательной моды подчиняется как закону сохранения энергии, так и закону сохранения квазиимпульса, причем последний сводится к сохранению волнового вектора.

Скорости нейтронов υ соответствует волновой вектор

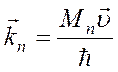
                                                     (4.23)

и кинетическая энергия 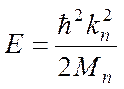                                                                (4.24)

Предположим, что при поглощении или рождении фонона энергия и волновой вектор нейтрона изменились и стали равными Е' и k_n′ соответственно. Тогда для угловой частоты из и волнового вектора К фонона, участвующего в процессе взаимодействия, будут выполняться  следующие законы сохранения:

,                                                                              (4.25)

.                                                                                  (4.26)

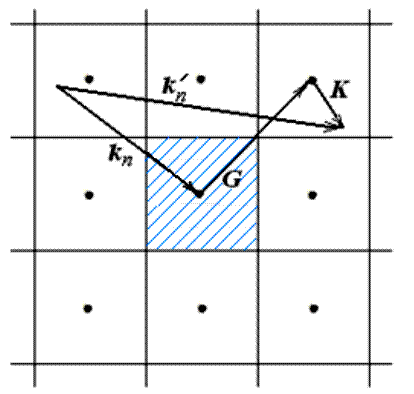(Напомним, что  – условие Вульфа-Брэгга, соответствующее упругому рассеянию на кристаллической решетке). Знак «плюс» соответствует процессу образования фонона, знак «минус» – процессу его исчезновения. Здесь вектор G равен либо нулю, либо вектору обратной решетки. Его можно включить в выражение (4.26), поскольку фонон с волновым вектором  К эквивалентен фонону с волновым вектором К + G. Закон сохранения волнового вектора в простейшем случае иллюстрируется рис. 4.10.

Исследование процессов неупругого рассеяния, описываемого выражениями (4.25) и (4.26), можно проводить  не только для нейтронов, но и для фотонов и для электронов. Однако из-за значительного различия скоростей света и звука лишь малая доля энергии фотонов может быть передана решетке (эффект рассеяния света на фононах в твердых телах или жидкостях известен как эффект рассеяния Мандельштама-Бриллюэна). Более удобными для этих исследований оказались тепловые нейтроны, поскольку в процессах неупругого рассеяния благодаря их относительно небольшим скоростям  (~ 10³ м/с) и энергии (0,1 – 0,01эВ) их волновой вектор претерпевает значительные изменения как по величине, так и по направлению.

Попытки изучения колебаний решетки с помощью неупругого рассеяния нейтронов возникли в начале 1950-х годов в связи с разработкой урановых реакторов – мощных источников медленных нейтронов. Этот метод оказался весьма полезным, и  в настоящее время имеются сведения о колебательных спектрах для многих твердых тел. Изменение скорости нейтрона вследствие рассеяния измеряется либо методами брэгговской дифракции, либо времяпролетными методами.

Вопрос 11

Число мод. Плотность состояний

В упругой среде могут возбуждаться любые колебания, однако число различающихся друг от друга типов колебаний решетки конечного размера из дискретных атомов строго ограниченно. Найдем распределение этих мод колебаний по частотам или волновым векторам.

Для того чтобы сделать это, рассмотрим сначала задачу об упругих колебаниях одномерной цепочки частиц; пусть (N + 1)  – число частиц, а – расстояние между ними, L – длина цепочки. Предположим, что частицы s = 0 и s = N  находятся на концах цепочки и закреплены, т.е   и . Тогда в этой цепочке могут возбудиться лишь такие продольные и поперечные колебания, для которых на длине Lуложится  1, 2, 3... или N  полуволн. Т.е. L = λ/2; 2λ/2; 3λ/2;… Nλ/2. Соответственно, волновые векторы этих разрешенных колебательных мод удовлетворяют соотношениям

,

или 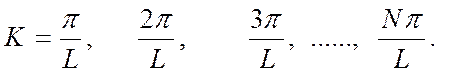                                   (4.27)

 В случае, когда К = π/L на длине L укладывается одна полуволна. Для  К = К_max = Nπ/L= π/a полуволна равна расстоянию а между атомами, в этом случае смещения не допускаются ни для одного атома.

Заметим, что эти колебания разделены одинаковыми интервалами . Разумеется, при больших N интервал очень мал, и при этом удобно ввести число состояний (число различимых колебательных мод). В случае одномерной цепочки частиц имеется одно нормальное колебание (мода) на каждый интервал значений К, равный  π/L, так что число мод на единичный интервал значений К равно L/π для К ≤ π/а  и нулю для К > π/а. Соответственно, в области от К до К+dKчисло состояний равно (L/π)dK.  Таким образом, число состояний для случая одномерной моноатомной цепочки имеет вид: