Спектр нормальных колебаний решетки, распределение колебаний по частотам. Понятие о фононах, страница 4

Как обсуждалось выше, связь между атомами твердого тела настолько сильная, что они не могут колебаться независимо друг от друга; N таких атомов образуют связанную систему, обладающую ЗN степенями свободы. В такой системе возникает в общем случае ЗN колебаний (N колебаний для каждого типа поляризации – одной продольной и двух поперечных мод), совершающихся с различными частотами. Эти колебания называются собственными колебаниями системы, а частоты, с которыми они совершаются, собственными частотами.

Модель Дебая дает значительно лучшее согласие с опытом, чем теория теплоемкости Энштейна.  В ней, как и в теории Эйнштейна, предполагается, фононы подчиняются распределению Планка и их средняя энергия может быть представлена соотношением (4.43). Важные дополнения к теории Эйнштейна состоят в том, что Дебай предположил:

·  колебания атомов в твердом теле не являются независимыми. Существуют зависимости частот собственных упругих колебаний от волнового вектора , причем в модели Дебая сделано упрощающее предположение, согласно которому учитываются только акустические типы колебаний  и выбирается простейший закон дисперсии (континуальное приближение);

·  частоты колебаний решетки ограничиваются максимальной частотой ω_D (см. (4.37)), так что выполняется соотношение

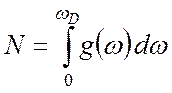                                            (4.50)

где 3N — полное число частот колебаний.

 Расчет теплоемкости кристаллической решетки в рамках теории Дебая проводится с учетом полученной им функции плотности собственных колебаний решетки g(ω) (см.(4.36)).

Энергию для каждого типа поляризации можно представить выражением 

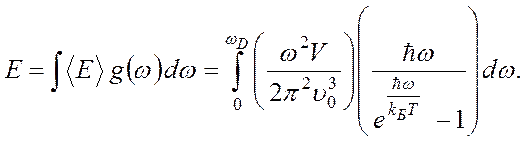                         (4.51)

Здесь ω_D – частота на которой обрезается непрерывный спектр.

Для простоты мы предполагаем, что скорости фононов для всех трех типов поляризации (одной продольной и двух поперечных мод) одинаковы, и поэтому, чтобы получить полную энергию, просто утроим энергию (4.51):

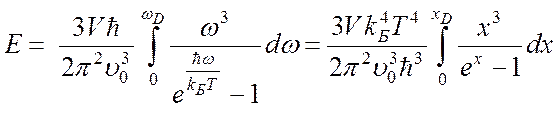                       (4.52)

где введены обозначения   и

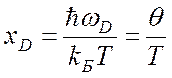                                            (4.53)

Соотношение (4.52) является определением температуры Дебая θ через предельную частоту ω_D, введенную условием (4.37). Для θ можно записать выражение

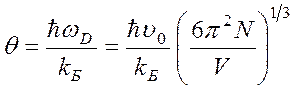                                         (4.54)

и переписать (4.52) в виде

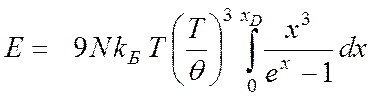 ,                               (4.55)

где  N – число атомов образца.

Теперь теплоемкость найти очень просто: нужно лишь продифференцировать по температуре первое из выражений для Е в  (4.52). Тогда получим:

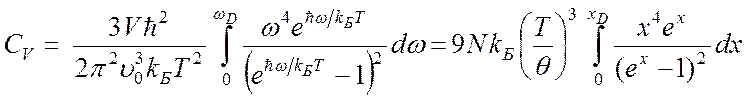.          (4.56)

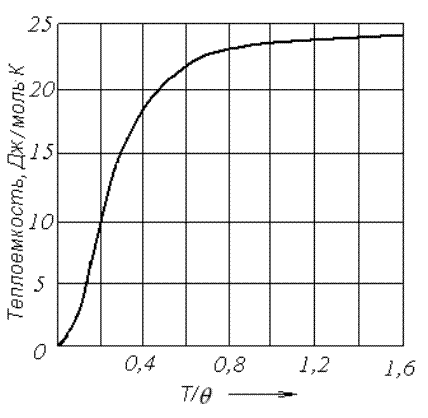
 График зависимости теплоемкости от отношения дан па рис. 4.14. Видно, что при высоких температурах молярная теплоемкость приближается к классическому значению .

Теплоемкость Дебая при высоких температурах

 При   Т >> θ       и знаменатель в подынтегральном выражении в формуле (4.55) можно разложить в ряд по малому параметру:

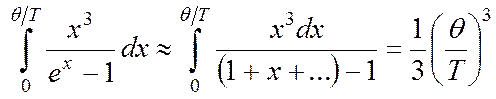.                              (4.57)

Подставляя результат (4.57) в (4.56) и принимая, что N = N_A, для теплоемкости в высокотемпературном пределе получим:

,

что, как и в теории Эйнштейна, соответствует закону Дюлонга и Пти.

Теплоемкость Дебая при низких температурах.

При очень низких температурах приближенное выражение для энергии можно получить из (4.55), положив верхний предел интеграла равным бесконечности. Тогда интеграл вычисляется, и равен:

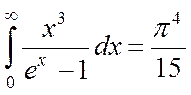                                       (4.58)

 Итак, для Е имеем:

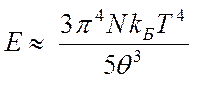        при   

а для теплоемкости C_V

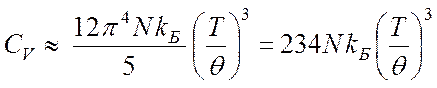                         (4.59)

Это и есть приближенный закон T ³ Дебая. Он хорошо выполняется при низких температурах, поскольку именно в этой области возбуждаются только низкоэнергетичные (длинноволновые) акустические фононы.

Формула Дебая оправдывается для большинства твердых тел.

Вопрос 15

Температура Дебая

Следует отметить, что понятие температуры Дебая используется во многих задачах физики твердого тела, в том числе и не связанных с теплоемкостью. Она является характеристической температурой твердого тела, зависящей от констант упругости. Физический смысл  температуры Дебая в том, что величина  представляет максимальный квант энергии, способный возбудить колебания решетки. При температуре выше температуры Дебая все фононы возбуждены, и  у большей части фононов длина волны имеет порядок нескольких межатомных расстояний (коротковолновые фононы). При температурах же значительно ниже дебаевской возбуждаются только фононы, волновые векторы К которых очень близки к центру зоны Бриллюэна и лежат достаточно далеко от ее границ (длинноволновые фононы).

Температура Дебая θ условно разделяет «квантово-механическую» и «классическую» области температурной зависимости физических свойств твердых тел. В первой из них (Т< θ) в результате температурного возбуждения происходит изменение числа фононов, во второй (Т> θ) — все фононы возбуждены.

Нужно отметить, что это представление вполне справедливо для кристаллов с одним атомом в базисе, где могут возбуждаться только акустические фононы. Однако кристаллы, содержащие два и более атома в базисе, дополнительно обладают оптическими модами. Поэтому для них при температурах выше θ продолжает происходить возбуждение фононов, теперь уже оптического типа.

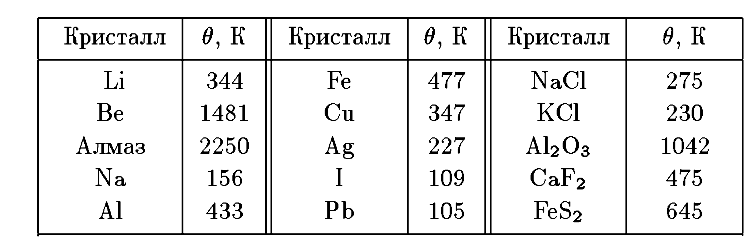
Как отмечалось выше, температура Дебая (так же, как и температура Энштейна) зависит от свойств вещества. Для большинства твердых тел она равна 100 – 400 К, хотя для таких веществ как бериллий, алмаз она аномально высока, что хорошо объясняется повышенной «жесткостью» межатомных связей. В табл. 4.2 приводятся значения температуры Дебая θ для некоторых кристаллов. Из таблицы  видно, что для кристаллов, у которых  θ < Т_комн, температуры больше комнатной являются сравнительно высокими. Поэтому для них отклонения от классических законов в этой области не слишком велики (большая часть или все фононы возбуждены). Иначе обстоит дело для кристаллов с высокой характеристической температурой, особенно в случае алмаза. Для последнего комнатная температура  существенно ниже дебаевской, и ни о какой применимости классических законов не может быть и речи. В таких кристаллах даже при комнатных температурах «вымерзают» все фононы, за исключением тех, длины волн которых очень велики по сравнению размерами элементарной ячейки. Теплоемкость алмаза уже при комнатных температурах следует закону Т³.

                                                                                                Таблица 4.2

Температура Дебая в для некоторых кристаллов