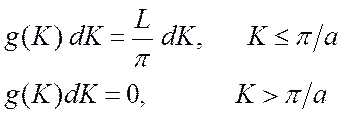Спектр нормальных колебаний решетки, распределение колебаний по частотам. Понятие о фононах, страница 2

.                           (4.28)

Здесь g(K) – плотность состояний (число состояний на единичный интервал К) в пространстве волновых чисел. Для одномерного случая мы получили, что g(K) не зависит от К в разрешенном спектральном интервале. Но для значительной части других, более сложных случаев g(K) имеет явную зависимость от К. Очевидно, что полное число разрешенных  состояний (собственных значений К в разрешенном интервале) равно N , т.е. числу атомов или элементарных ячеек в цепочке.

Имеется и другой прием подсчета числа состояний, часто используемый и по существу вполне эквивалентный. В нем в качестве граничных условий выбирают периодические граничные условия (условия Борна-Кармана), в соответствии с которыми смещения должны удовлетворять условию цикличности . В случае больших систем он ни в чем существенном не меняет физики задачи. При этом по цепочке распространяются бегущие волны и разрешенные значения К таковы:

                        (4.29)

Где знаки плюс и минус соответствуют волнам, распространяющимся в противоположные стороны. Этот подход дает то же число состояний (по одному на способный смещаться атом), что и описанный выше способ, но теперь К принимает как положительные, так и отрицательные значения, а интервалы между соседними значениями К одинаковы и равны. В случае периодических граничных условий число мод на единичный интервал значений К равно L/2π для К в интервале – π/а ≤ К ≤ π/а и нулю для всех остальных значений К. Если для удобства расчета мы хотим ограничиться положительными значениями К, то опять придем к значению L/π.

В задачах физики твердого тела нередко встречаются случаи, когда необходимо знать зависимость плотности состояний не от К, а от каких-то других переменных. Например, во многих случаях необходимо иметь не только зависимость g(K), но и g(ω). Для линейной одноатомной цепочки можно записать

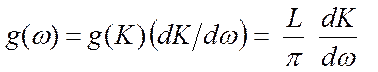.                            (4.30)

Групповую скорость мы можем получить из закона дисперсии (4.5)

, 

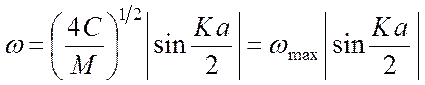где   – максимально возможная частота колебаний в цепочке. Отсюда

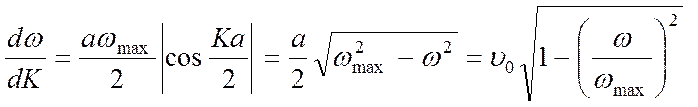            (4.31)

Подставляя это выражение в (4.30), получим

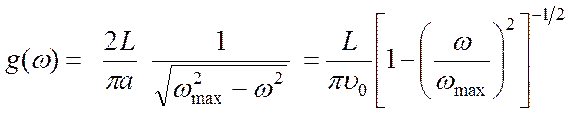  ,                       (4.32)

где 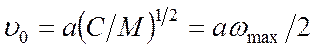 – постоянная скорость звука (см. формулу (4.7)). Таким образом, функция  g(ω) имеет явную зависимость от ω и обращается в бесконечность на верхнем пределе, то есть в тех случаях, когда график функции ω(К) идет горизонтально (на горизонтальном участке групповая скорость равна нулю).

В приближении Дебая, когда среду можно считать непрерывной  (Ka<<1), полагают  (см. (4.7)), так что  . В одномерном случае из (4.31) для  получим:

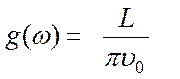при 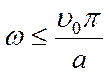                                       (4.33)

и g(ω) = 0 в остальных случаях. Спектр обрезается при чтобы полное число нормальных колебаний было  правильным, т. е. равным  N – числу частиц в цепочке.

 График функции g(ω), соответствующий выражениям (4.32) и (4.33) приведен на рис. 4.11. Видно, что для цепочечной модели имеет место особенность, которая в дебаевском приближении отсутствует.

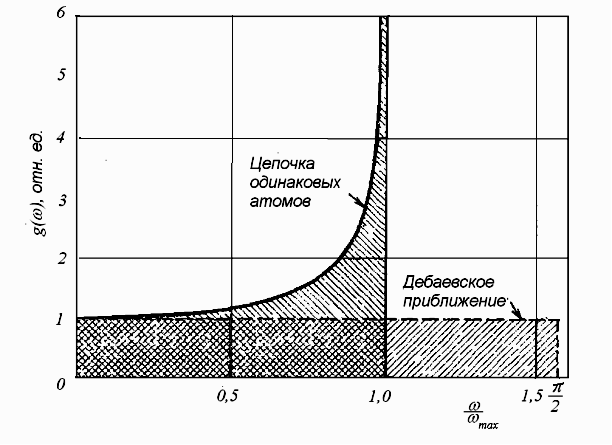В случае одномерной цепочки, составленной из атомов двух сортов, для акустической ветви функция плотности мод будет подобна (4.31); для оптической ветви (той же цепочки) функция плотности мод имеет особенности на предельных (верхнем и нижнем) значениях частот.

Плотность мод в трехмерном случае. Рассмотрим трехмерный случай, когда модель кристалла представляет собой куб со стороной L, содержащий N  элементарных ячеек, и применим периодические граничные условия. Нетрудно показать, что на объем в К- пространстве приходится одно разрешенное значение К, и поэтому число разрешенных мод на единицу объема в К- пространстве (для каждой ветви и данной поляризации) равно

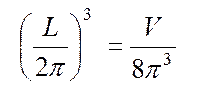.                                           (4.34)

где V = L³ — объем кристалла.

В случае трехмерного кристалла вывод зависимости g(ω) оказывается значительно более сложным, чем для одномерного кристалла. Ограничимся только континуальным (дебаевским) приближением. В этом случае скорость звука считается постоянной: . Полное число N мод с волновым вектором, меньшим  К, согласно (4.34) равно произведению объема сферы радиуса К на число мод, приходящихся на единицу объема в К- пространстве, т. е. на; итак, для каждого типа поляризации имеем:

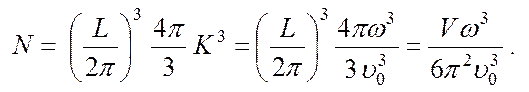                          (4.35)

Следовательно, плотность мод g(ω) для каждого типа поляризации равна

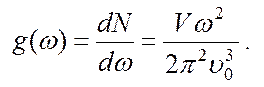                                      (4.36)

Если образец содержит N элементарных ячеек, то общее число мод акустических фононов (данного типа поляризации) равно N, и частота ω_D, на которой обрезается непрерывный спектр, определяется  из соотношения (4.35):

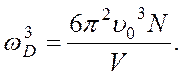                                          (4.37)

Для волнового числа K_D, соответствующего ω_D, имеем:

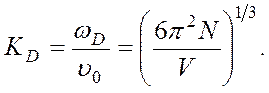                                    (4.38)

В модели Дебая исключены моды с волновыми векторами, длины которых больше K_D; число мод, имеющих К ≤K_D, исчерпывает число степеней свободы моноатомной решетки.

Итак, в дебаевском приближении мы не только заменяем истинную плотность мод величиной (4.36), которая получилась как следствие линейного дисперсионного закона , но и заменяем сферой область интегрирования в К-пространстве, которая, строго говоря, должна была бы быть зоной Бриллюэна.

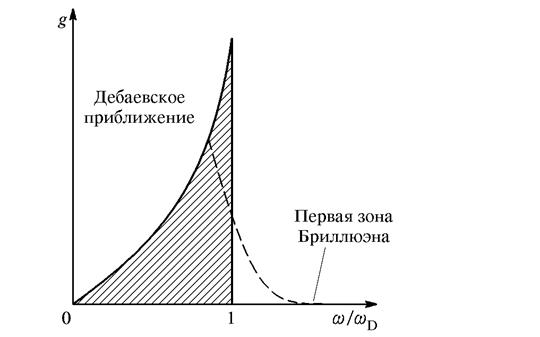
Плотность мод (4.36) для дебаевского приближения в случае трехмерного кристалла изображена на рис. 4.12. Там же показан ход этой функции в случае «правильной» области интегрирования (зоны Бриллюэна) для простой кубической решетки. Если, например, υ₀ = 5000 м/с и N/L³ = 10²⁹ атомов на 1 м³, то

                 ω_D ≈ 10¹⁴ рад/с,         K_D ≈ 2^.10¹⁰ м ^-1                           (3.39)

Вопрос 12

Теплоемкость кристаллической решетки

Тема 4.2. Теплоёмкость решётки, модели Эйнштейна и Дебая. Ангармонические взаимодействия в кристаллах, коэффициент теплового расширения. Коэффициент теплопроводности.

Говоря о теплоемкости, мы обычно будем иметь в виду теплоемкость при постоянном объеме С_V, которая является более фундаментальной величиной, чем теплоемкость при постоянном давлении С_р, которую обычно определяют в экспериментах (относительная величина разности между ними невелика и ею часто можно пренебречь).

Теплоемкость при постоянном объеме определяется соотношением