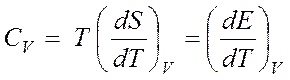Спектр нормальных колебаний решетки, распределение колебаний по частотам. Понятие о фононах, страница 3

,                                        (4.39)

где S — энтропия, Е — внутренняя энергия, Т — абсолютная температура.

Экспериментальные факты, относящиеся к теплоемкости типичных неорганических твердых тел, можно резюмировать в следующих пунктах:

1. При комнатных температурах значения молярной теплоемкости почти всех твердых тел близки к

2. При низких температурах теплоемкость заметно уменьшается и в области абсолютного нуля температур приближается к нулю по закону Т³ для диэлектриков и по закону Т для металлов. Если металл переходит в сверхпроводящее состояние, то закон уменьшения теплоемкости более резкий, чем Т.

Классическая теория теплоемкости твердых тел.

Закон Дюлонга и Пти

В классической теории теплоемкости однородное твердое тело рассматривается как совокупность совершенно независимых друг от друга частиц, совершающих колебания с одной и той же частотой ν. Каждая такая частица обладает 3 степенями свободы. На каждую степень свободы приходится в среднем  кинетической энергии и   потенциальной энергии (k_Б – постоянная Больцмана). Поэтому средняя энергия колеблющейся частицы – классического осциллятора – равна . Энергия одного моля вещества, содержащего N_А  частиц, равна:

,                                           (4.40)

где R— универсальная газовая постоянная. Дифференцируя (4.40) по Т, получим молярную теплоемкость твердого тела при постоянном объеме (С_V):

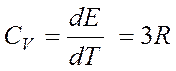                                              (4.41)

Так как R = 8,31дж/кмольK, то

                               (4.42)

Молярная теплоемкость одноатомных твердых тел равна, таким образом, примерно . Этот закон был установлен экспериментально Дюлонгом и Пти еще в 1819 г. В табл. 4.1 приведены  молярные теплоемкости  ряда веществ при обычных температурах.

Таблица 4.1

	Na	Al	Fe	Ni	Cu	Zn	Sn	Pt	Pb	Cd	B	C
	27	23,5	24,7	24,7	23,5	24	25,5	24,7	24,7	24,7	14,2	5,7

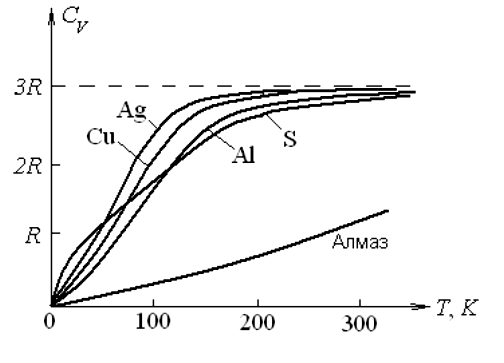Из таблицы видно, что в подавляющем большинстве случаев закон Дюлонга и Пти оправдывается достаточно хорошо. Однако у алмаза и бора теплоемкость при комнатной температуре оказалась значительно ниже С понижением температуры такое отступление от закона Дюлонга и Пти наблюдается у всех твердых тел (рис. 4.13). При приближении к абсолютному нулю их теплоемкость стремится к нулю, в то время как, согласно классической теории она не должна зависеть от температуры (пунктирная прямая на рис. 4. 13).

Неудовлетворительность классической теории теплоемкости обусловлена двумя причинами. Во-первых, в этой теории предполагается, что атомы твердого тела колеблются независимо друг от друга с одной и той же частотой. В действительности же атомы в твердом теле связаны настолько прочно, что образуют единую систему, обладающую широким спектром собственных частот колебаний (что было показано выше). Во-вторых, колеблющийся атом следует уподоблять не классическому, а квантовому осциллятору, обладающему дискретным энергетическим спектром. Среднее значение энергии таких осцилляторов выражается формулой Планка, которая должна заменить для них закон равномерного распределения энергии по степеням свободы.

Дальнейшее развитие теории теплоемкости твердых тел шло по пути преодоления этих недостатков.

Вопрос 13

Квантовая теория теплоемкости твердых тел по Эйнштейну

Как и в классической теории, в теории Эйнштейна твердое тело рассматривается как совокупность N  независимых атомов, колеблющихся с одной и той же частотой ω_Е. Однако средняя энергия, приходящаяся на одну степень свободы (соответствующая одной колебательной моде), полагается равной не , а вычисляется по формуле Планка для средней энергии линейного квантового осциллятора:

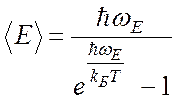 .                                      (4.43)

Частоту  ω_Е. Энштейн использовал в качестве подгоночного параметра для согласования своей модели теплоемкости с экспериментальными данными для твердых тел.

 Энергия  одного моля, имеющего  3N_А  степеней  свободы (соответственно, 3N_А колебательных мод для трех типов поляризации),  равна:

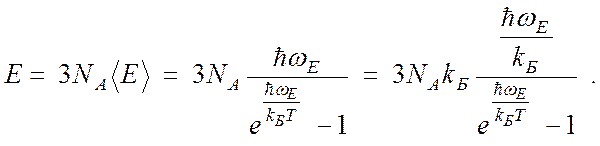                (4.44)

Величину                                  ,                                             (4.45)

имеющую размерность температуры, Эйнштейн назвал характеристической температурой тела. Из формулы (4. 45) видно, что θ непосредственно связана с частотой колебаний атомов твердого тела и является, таким образом, константой, характерной для него. Пользуясь (4.45), формулу (4.44) можно представить в следующем виде:

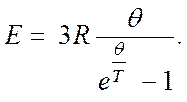                                          (4.46)

Дифференцируя (4.46) по температуре, получим

 

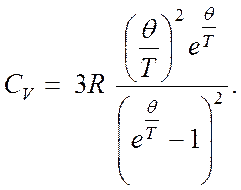                                        (4.47)

Формула (4.47) имеет ряд преимуществ перед формулой (4.41). При низких температурах ()  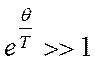, вследствие чего единицей в знаменателе формулы (4.47) можно пренебречь и записать ее в следующем виде:

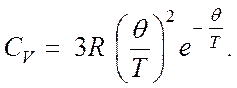                                       (4.48)

При 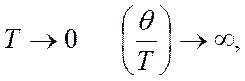 а 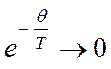.  Так как  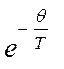убывает значительно быстрее, чем  растет 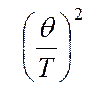, то

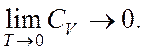                                              (4.49)

Согласно теории Энштейна, теплоемкость кристаллической решетки убывает при по закону ~ , тогда как эксперимент, как известно, дает для диэлектриков (решеточного вклада в теплоемкость) закон ~ Т ³. С другой стороны, в области высоких температур, в которой выполняется закон Дюлонга и Пти, формула (4.47) переходит в формулу (4.41). Это свидетельствует о качественном согласии теории Эйнштейна с опытом. Количественно же эта теория расходится с опытом особенно в области низких температур. Ограниченность модели Эйнштейна состоит в том, что его предположение о равенстве частот всех упругих волн в твердом теле является слишком сильным. Но тем не менее главное, что хотел показать и показал Эйнштейн, состоит в том, что колебания механических осцилляторов нужно квантовать точно так же, как Планк квантовал осцилляторы излучения. Эйнштейн, применив модель твердого тела как системы осцилляторов, убедительно объяснил, почему при теплоемкость твердых тел резко уменьшается до нуля.

Вопрос14

Теория теплоемкости решетки по Дебаю.