ЛЕКЦИЯ 10
Энергия Ферми и эффективная масса электрона. Плотность электронных состояний. Классификация твёрдых тел по типу энергетических зон
Движение свободного электрона под действием внешнего поля
Поместим свободный электрон,
обладающий массой т и зарядом ‒ е, в электрическое поле с
напряженностью Е. Это поле действует на электрон с силой
![]() направленной против поля. В соответствии
со вторым законом Ньютона электрон получит ускорение
направленной против поля. В соответствии
со вторым законом Ньютона электрон получит ускорение ![]() . Как
и сила F, ускорение а направлено против поля. Энергия электрона,
движущегося со скоростью υg, равна:
. Как
и сила F, ускорение а направлено против поля. Энергия электрона,
движущегося со скоростью υg, равна:
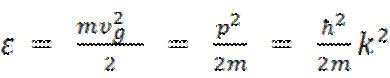 (5.12)
(5.12)
где р —
импульс электрона связанный с волновым числом kсоотношением:
![]() . Графически зависимость εот kвыражается параболой (см. рис. 5.1).
. Графически зависимость εот kвыражается параболой (см. рис. 5.1).
Движение электрона в периодическом поле кристалла под действием внешнего поля. Эффективная масса электрона
Рассмотрим теперь движение
электрона, находящегося в периодическом поле кристалла, под действием
внешнего поля Е. Как
и в случае свободного электрона, это поле действует на электрон, находящийся в периодическом поле, с силой ![]() , направленной против поля. Однако для свободного электрона эта
сила является единственной силой, определяющей характер его движения. На
электрон же, находящийся в периодическом поле, помимо внешней силы действуют значительно более мощные внутренние силы, создаваемые полем кристалла. Поэтому результирующее движение электронов
в кристалле является значительно более сложным, чем движение свободных электронов. Для описания этого движения поступим
следующим образом.
, направленной против поля. Однако для свободного электрона эта
сила является единственной силой, определяющей характер его движения. На
электрон же, находящийся в периодическом поле, помимо внешней силы действуют значительно более мощные внутренние силы, создаваемые полем кристалла. Поэтому результирующее движение электронов
в кристалле является значительно более сложным, чем движение свободных электронов. Для описания этого движения поступим
следующим образом.
Определим элементарную работу dA, которую совершает внешняя сила F, действуя на электрон в течение
времени dt. За время dtэлектрон проходит путь![]() , где υg — скорость
электрона, равная групповой скорости распространения электронных волн:
, где υg — скорость
электрона, равная групповой скорости распространения электронных волн: ![]() . На пути dх сила Fпроизводит элементарную работу dA, равную:
. На пути dх сила Fпроизводит элементарную работу dA, равную: ![]() . Для электронных волн
. Для электронных волн ![]() где ε — собственное
значение энергии электрона.
где ε — собственное
значение энергии электрона.
Поэтому групповая скорость 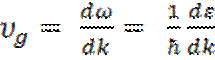 . Подставляя это значение
υg в выражение для
dA, получим:
. Подставляя это значение
υg в выражение для
dA, получим:
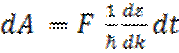 . (5.13)
. (5.13)
Совершая работу dA, внешняя сила меняет энергию электрона на dε(dA= dε). Отсюда следует:
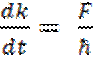 (5.14)
(5.14)
Дифференцируя υg по времени,
будем иметь: 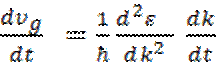
Подставляя
![]() из (5.13), получим:
из (5.13), получим:
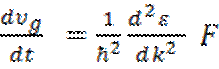 илиa
илиa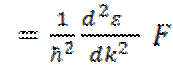 (5.15)
(5.15)
Формула (5.15) устанавливает связь между ускорением, с которым движется электрон, находящийся в периодическом поле кристалла, и внешней силой F, действующей на электрон со стороны внешнего поля Е. Она выражает, следовательно, второй закон Ньютона. Из этой формулы следует, что под действием внешней силы Fэлектрон в периодическом поле кристалла двигается в среднем так, как двигался бы под действием этой силы свободный электрон, если бы он обладал массой
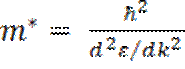 ,
(5.16)
,
(5.16)
m* называется эффективной массой электрона. Приписывая электрону, находящемуся в периодическом поле кристалла, массуm* , мы можем считать этот электрон свободным и описывать его движение во внешнем поле так, как мы описываем движение обычного электрона.
Для свободного электрона энергия 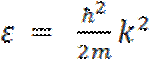 является квадратичной функцией от
волнового числа и графически выражается параболой (см. рис. 5.1). Вторая
производная от εпо kвыражает кривизну параболы у начала
координат (при k = 0). Она равна
является квадратичной функцией от
волнового числа и графически выражается параболой (см. рис. 5.1). Вторая
производная от εпо kвыражает кривизну параболы у начала
координат (при k = 0). Она равна 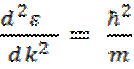 . Подставляя это
значение
. Подставляя это
значение 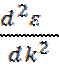 в формулу (5.16), получим:
в формулу (5.16), получим:
m* = m. (5.17)
Как и следовало ожидать, для свободного электрона эффективная масса равна просто массе электрона.
Для электрона, находящегося
в периодическом поле, энергия является значительно более сложной функцией
волнового числа k (рис. 5.4, 5.5,
5.6).Только в области, близкой к k= 0,
кривая, выражающая зависимость ε от k
для электрона, находящегося в периодическом поле, практически сливается с
параболой для свободного электрона. По мере же приближения к вершине зоны (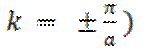 кривая все сильнее и сильнее отклоняется
от параболы. Поэтому эффективная масса электронов, располагающаяся у дна
энергетической зоны, должна мало отличаться от массы свободных электронов. Для
электронов же, размещающихся на более высоких энергетических уровнях, это
различие может быть весьма сильным.
кривая все сильнее и сильнее отклоняется
от параболы. Поэтому эффективная масса электронов, располагающаяся у дна
энергетической зоны, должна мало отличаться от массы свободных электронов. Для
электронов же, размещающихся на более высоких энергетических уровнях, это
различие может быть весьма сильным.
 Чтобы
проиллюстрировать характер изменения эффективной массы электрона по мере
поднятия его на все более высокие энергетические уровни энергетической зоны,
рассмотрим следующий идеализированный пример. Предположим, что в первой зоне
кристалла (рис. 5.7) находится один единственный электрон, располагающийся на
самом низком уровне.
Чтобы
проиллюстрировать характер изменения эффективной массы электрона по мере
поднятия его на все более высокие энергетические уровни энергетической зоны,
рассмотрим следующий идеализированный пример. Предположим, что в первой зоне
кристалла (рис. 5.7) находится один единственный электрон, располагающийся на
самом низком уровне.
 Приложим к кристаллу
внешнее поле Е.
Действуя на электрон с силой
Приложим к кристаллу
внешнее поле Е.
Действуя на электрон с силой ![]() , это поле будет ускорять его, энергия
электрона будет увеличиваться, и он как по ступенькам будет переходить на все
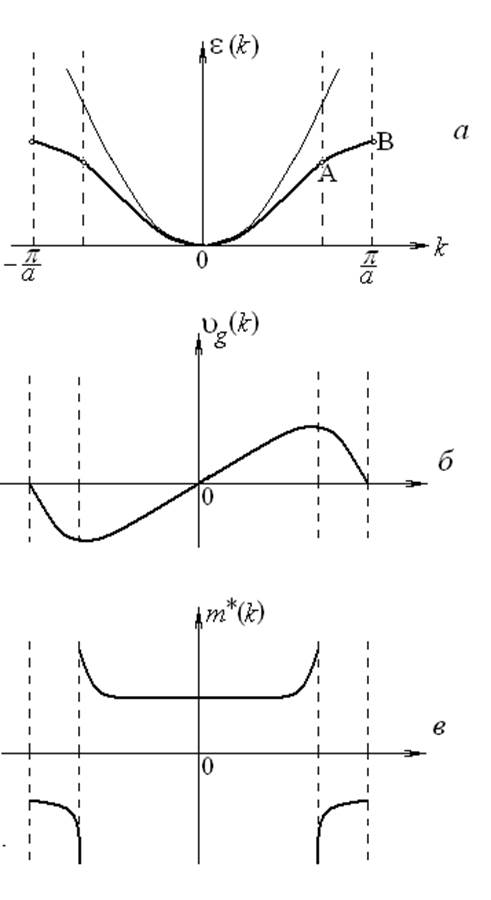
более высокие энергетические уровни зоны. На рис. 5.7 показана зависимость от
волнового числа k кинетической
энергии электрона ε (рис. 5.7, а), скорости его
движения (рис. 5.7, б) и эффективной массы
, это поле будет ускорять его, энергия
электрона будет увеличиваться, и он как по ступенькам будет переходить на все
более высокие энергетические уровни зоны. На рис. 5.7 показана зависимость от
волнового числа k кинетической
энергии электрона ε (рис. 5.7, а), скорости его
движения (рис. 5.7, б) и эффективной массы 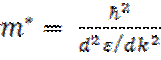 (рис. 5.7, в). При небольших
значениях к кривая ε (k)
сливается с параболой
(рис. 5.7, в). При небольших
значениях к кривая ε (k)
сливается с параболой 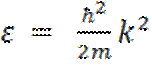 и скорость движения электрона
и скорость движения электрона ![]() линейно увеличивается с ростом k, а эффективная масса остается постоянной и
приблизительно равной массе свободного электрона: m*
линейно увеличивается с ростом k, а эффективная масса остается постоянной и
приблизительно равной массе свободного электрона: m* ![]() m. Такой электрон
ведет себя нормально, как частица, обладающая отрицательным зарядом «− е» и
положительной эффективной массой m* .
m. Такой электрон
ведет себя нормально, как частица, обладающая отрицательным зарядом «− е» и
положительной эффективной массой m* .
По мере удаления
от начала координат кривая ε (k)
постепенно отходит от параболы, нарастание скорости с увеличением к замедляется
и эффективная масса электрона увеличивается. Точка А является точкой
перегиба кривой ε(k). В этой точке
первая производная ![]() достигает экстремума, а вторая
производная обращается в нуль. Поэтому в точке А скорость достигает
максимального значения, а эффективная масса электрона обращается в
бесконечность. При переходе через точку А эффективная масса меняет знак:
она становится отрицательной. Это означает, что при дальнейшем увеличении
k скорость
электрона не только не увеличивается, а наоборот, уменьшается, хотя направление
внешней силы остается неизменным. В точке В скорость обращается в нуль:
электрон останавливается, несмотря на то, что его импульс
достигает экстремума, а вторая
производная обращается в нуль. Поэтому в точке А скорость достигает
максимального значения, а эффективная масса электрона обращается в
бесконечность. При переходе через точку А эффективная масса меняет знак:
она становится отрицательной. Это означает, что при дальнейшем увеличении
k скорость
электрона не только не увеличивается, а наоборот, уменьшается, хотя направление
внешней силы остается неизменным. В точке В скорость обращается в нуль:
электрон останавливается, несмотря на то, что его импульс ![]() достигает максимального значения,
равного:
достигает максимального значения,
равного: ![]() . Здесь электрон испытывает брэгговское
отражение от решетки, его волновой вектор меняется от
. Здесь электрон испытывает брэгговское
отражение от решетки, его волновой вектор меняется от ![]() до
до ![]() и он появляется в точке В'. В
интервале от В' до А' электрон ускоряется в направлении, противоположном
действию силы F, и его скорость
меняется от 0 до максимального отрицательного значения, а эффективная масса
— от —m* до
— ∞. В точке перегиба А' знак эффективной массы меняется с
отрицательного на положительный и в интервале от А' до 0 электрон
ускоряется «нормально» в направлении действующей силыF,
скорость постепенно увеличивается до нуля, а эффективная масса достигает
постоянного положительного значения m*. Таким образом, по мере увеличения энергии
электрона и перемещения его от дна зоны к ее вершине эффективная масса меняется
не только по величине, но и по знаку. Это указывает на то, что поведение во
внешнем поле электронов, находящихся на разных энергетических уровнях зоны,
может быть весьма различным и сильно отличаться от поведения свободных электронов.
и он появляется в точке В'. В
интервале от В' до А' электрон ускоряется в направлении, противоположном
действию силы F, и его скорость
меняется от 0 до максимального отрицательного значения, а эффективная масса
— от —m* до
— ∞. В точке перегиба А' знак эффективной массы меняется с
отрицательного на положительный и в интервале от А' до 0 электрон
ускоряется «нормально» в направлении действующей силыF,
скорость постепенно увеличивается до нуля, а эффективная масса достигает
постоянного положительного значения m*. Таким образом, по мере увеличения энергии
электрона и перемещения его от дна зоны к ее вершине эффективная масса меняется
не только по величине, но и по знаку. Это указывает на то, что поведение во
внешнем поле электронов, находящихся на разных энергетических уровнях зоны,
может быть весьма различным и сильно отличаться от поведения свободных электронов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.