Энергия Ферми и эффективная масса электрона. Плотность электронных состояний. Классификация твёрдых тел по типу энергетических зон, страница 2

Понятие эффективной массы электрона является лишь удобным способом описания движения электрона, находящегося в периодическом поле кристалла, под действием внешнего электрического поля. Сама же эффективная масса не является массой в обычном смысле этого слова. Она не определяет ни запаса энергии, ни инерционных, ни гравитационных свойств электрона. По величине она может быть как больше, так и меньше истинной массы электрона. Более того, m* может быть как положительной, так и отрицательной. Эффективная масса является лишь коэффициентом пропорциональности в соотношении (5. 15), связывающем внешнюю силу с ускорением движения электрона. Она имеет смысл лишь до тех пор, пока энергия электрона ε может быть выражена как квадратичная функция волнового числа. В этом случае m* сохраняется постоянной. Из рис. 5. 7 видно, что это имеет место при k, отвечающем дну и вершине энергетической зоны. В первом случае m* 7 видно, что это имеет место при k, отвечающем дну и вершине энергетической зоны. >0, во втором m* <0. Вблизи же точек перегиба m* перестает быть аналогом массы.  К счастью,  практически всегда приходится иметь дело с электронами, располагающимися или дна зоны или у ее вершины. К этим электронам вполне применимо понятие эффективной массы, чем и оправдывается введение этого понятия.

Характерной особенностью эффективной массы в кристалле является то, что ее величина зависит не только от состояния электрона (положения в энергетической зоне), но и от направления движения электрона. Зависимость эффективной массы от направления движения электрона объясняется анизотропией кристалла: при движении электрона силы взаимодействия его с кристаллической решеткой различны в различных кристаллографических направлениях. Причем в твердом теле с сильно анизотропной кристаллической структурой m* может быть положительной для одних направлений и отрицательной для других.

Понятие о дырках

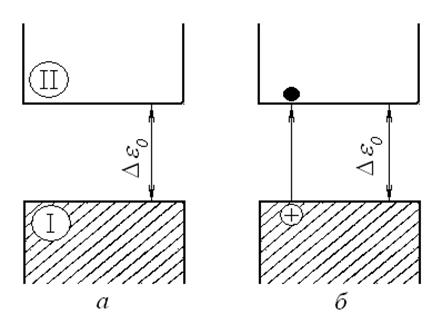
Предположим, что данная энергетическая зона целиком заполнена электронами (рис. 5.8 а). Электроны, располагающиеся на верхних уровнях зоны, обладают отрицательной эффективной массой (ускоряются в направлении, противоположном действию внешней силы) и отрицательным зарядом — е. Удалим с одного из таких уровней электрон (5.8,б). Так как зона была целиком заполнена отрицательно заряженными электронами, то освобожденный уровень,  не укомплектованный электроном, будет вести себя как частица, обладающая положительным зарядом, численно равным заряду электрона + е.  Кроме того, так как электроны верхних уровней зоны  обладают   отрицательной эффективной массой, то освобожденный уровень будет вести себя как частица, обладающая положительной эффективной массой, численно равной эффективной массе электрона, занимающего этот уровень. Таким образом, освобождение одного из верхних уровней занятой энергетической зоны эквивалентно появлению в ней частицы, обладающей положительным зарядом и положительной эффективной массой. Такую фиктивную частицу называют дыркой.

Дырки играют исключительно важную роль в определении электрических свойств твердых тел. В телах, имеющих почти целиком заполненные энергетические зоны, электрический ток возникает в результате направленного движения дырок. Такой дырочной проводимостью обладает, в частности, ряд металлов. Но особенно большое значение дырочный механизм проводимости имеет в полупроводниках.

         Заполнение зон электронами

Каждая энергетическая зона содержит, как мы выяснили, ограниченное число энергетических уровней. В соответствии с принципом Паули на каждом таком уровне может разместиться не более двух электронов с противоположно направленными спинами. При ограниченном числе электронов, содержащихся в твердом теле, заполненными окажутся лишь несколько наиболее низких энергетических  зон.

Рассмотрим более подробно процесс заполнения зон электронами, когда эти зоны не перекрываются. Зависимость энергии электрона от волнового числа для этого случая изображена на рис. 5. 6. При небольших значениях k(вблизи начала координат) кривая ε (k) представляет собою  параболу :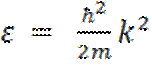

Вследствие этого электроны, заполняющие энергетические уровни, располагающиеся у дна зоны, ведут себя как свободные электроны с эффективной массой m*. Поэтому их распределение по энергиям, как и распределение свободных электронов, подчиняется статистике Ферми - Дирака. Именно число электронов в единице объема твердого тела dп, энергия которых заключена в пределах от ε до ε + dε равно

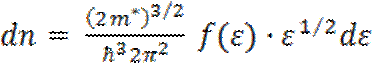                                      (5.18)

где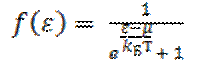– функция Ферми –Дирака, µ - химический потенциал, отнесенный к одной частице,k_Б– постоянная Больцмана, Т – абсолютная температура.

Подробнее функция распределения  Ферми –Дирака будет обсуждаться позже. Пока лишь отметим, что в системе электронов металла при абсолютном нуле он совпадает с уровнем Ферми (µ = ε_F). Но неверно считать уровень химического потенциала уровнем Ферми во всех остальных случаях. Уровнем Ферми называют реальное одноэлектронное состояние,  которым заканчивается заполнение энергетических состояний при абсолютном нуле. В чистом полупроводнике уровень Ферми совпадает с потолком валентной зоны. А химический потенциал при малых температурах лежит вблизи центра запрещенных энергий между валентной зоной и зоной проводимости.

 При  абсолютном нуле для состояний с ε < µ   f(ε) = 1 и

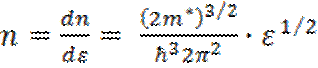                                           (5.19)

На рис. 5.9 представлена кривая зависимости числа электронов в зоне от энергии ε. Участок Оdэтой кривой отвечает формуле (5.19) и соответствует распределению по энергиям свободных электронов с эффективной массой т*.

По мере заполнения зоны квадратичная зависимость энергии электронов от волнового числа, характерная для свободных электронов, выполняется все хуже и хуже (рис.5.6), и кривая зависимости п от εотходит от параболы, выраженной уравнением (5. 19).