 Точка а соответствует
значению
Точка а соответствует
значению 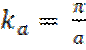 , при котором достигается граница зоны для направления а в
кристалле. В этой точке исчерпываются энергетические состояния, отвечающие
направлению
, при котором достигается граница зоны для направления а в
кристалле. В этой точке исчерпываются энергетические состояния, отвечающие
направлению ![]() . При дальнейшем увеличении ε исчерпываются
энергетические состояния, отвечающие направлениям
. При дальнейшем увеличении ε исчерпываются
энергетические состояния, отвечающие направлениям ![]() ,
,![]() и т. д. Поэтому, начиная от
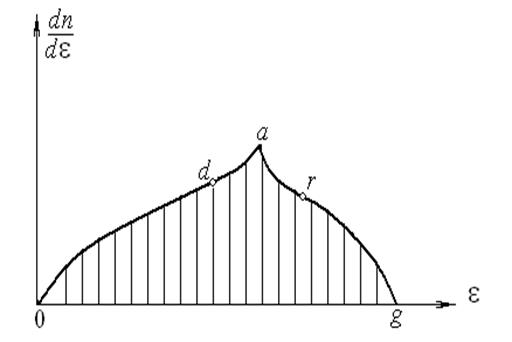
и т. д. Поэтому, начиная от  точки а, кривая зависимости п от ε снижается
и в точке g, отвечающей наиболее высоким энергетическим уровням зоны, обращается в нуль. Так как у вершины энергетической зоны квадратичная зависимость
энергии от волнового числа снова имеет место, но уже теперь для дырок, то участок grкривой
распределения будет также параболическим, как и участок Оd.
точки а, кривая зависимости п от ε снижается
и в точке g, отвечающей наиболее высоким энергетическим уровням зоны, обращается в нуль. Так как у вершины энергетической зоны квадратичная зависимость
энергии от волнового числа снова имеет место, но уже теперь для дырок, то участок grкривой
распределения будет также параболическим, как и участок Оd.
 Такую форму
имеет кривая распределения электронов по энергиям для целиком заполненной зоны.
Если число электронов значительно меньше числа уровней, содержащихся в зоне, то
кривая распределения оборвется в какой-либо точке участка Оdи при абсолютном
нуле будет иметь вид, показанный на рис. 5.10, а. Все уровни, лежащие левее
уровня Ферми εF, целиком заполнены
электронами, уровни же, расположенные правее уровня Ферми, совершенно
свободны. При температуре, отличной от абсолютного нуля, участок кривой распределения,
прилегающий к уровню Ферми, расплывается
Такую форму
имеет кривая распределения электронов по энергиям для целиком заполненной зоны.
Если число электронов значительно меньше числа уровней, содержащихся в зоне, то
кривая распределения оборвется в какой-либо точке участка Оdи при абсолютном
нуле будет иметь вид, показанный на рис. 5.10, а. Все уровни, лежащие левее
уровня Ферми εF, целиком заполнены
электронами, уровни же, расположенные правее уровня Ферми, совершенно
свободны. При температуре, отличной от абсолютного нуля, участок кривой распределения,
прилегающий к уровню Ферми, расплывается 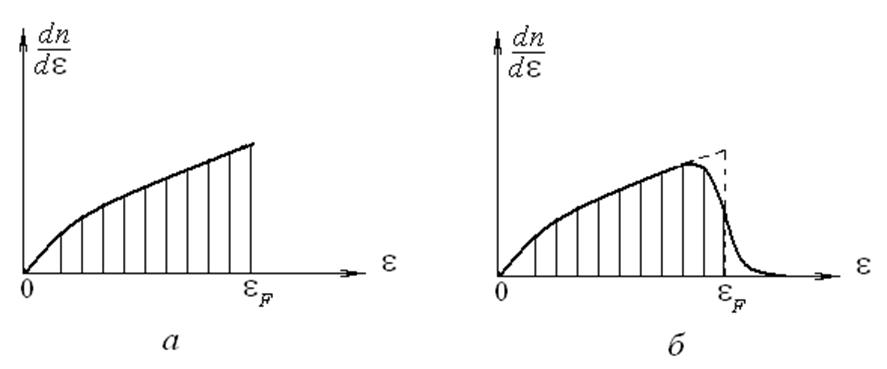 и приобретает
вид, показанный на рис. 5.10, б. На рис. 5.11 представлен случай, когда две соседние зоны перекрываются. Так
как электроны всегда занимают наиболее
низкие энергетические уровни, то часть их перейдет с более
и приобретает
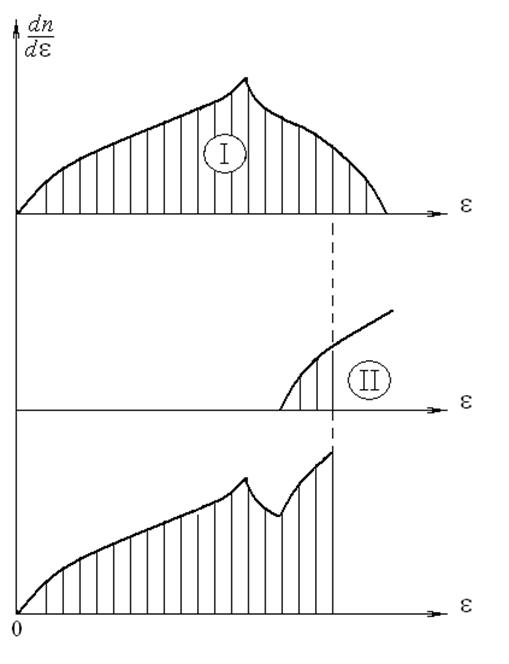
вид, показанный на рис. 5.10, б. На рис. 5.11 представлен случай, когда две соседние зоны перекрываются. Так
как электроны всегда занимают наиболее
низкие энергетические уровни, то часть их перейдет с более
высоких уровней зоны I на более низкие уровни зоны II, и обе зоны окажутся укомплектованными неполностью. По характеру заполнения зон электронами все твердые тела можно разделить на три класса.
 Первый класс тел содержит только целиком заполненные и
совершенно
свободные энергетические
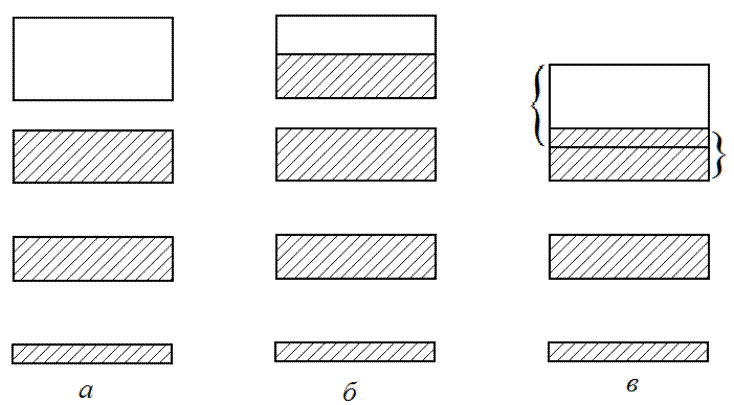
зоны. На рис. 5.12, а занятые зоны заштрихованы, свободные — оставлены
пустыми.
Первый класс тел содержит только целиком заполненные и
совершенно
свободные энергетические
зоны. На рис. 5.12, а занятые зоны заштрихованы, свободные — оставлены
пустыми.
У второго класса тел над целиком заполненными нижними зонами располагается зона, укомплектованная лишь частично: у нее заняты только нижние энергетические уровни, располагающиеся у дна зоны (рис. 5.12, б).
 Наконец, у
третьего класса тел верхняя целиком заполненная зона перекрывается с
расположенной над ней свободной зоной (рис. 5.12, в). Такое перекрытие приводит,
как мы видели, к тому, что обе эти зоны
оказываются укомплектованными лишь частично (рис.5.11).
Наконец, у
третьего класса тел верхняя целиком заполненная зона перекрывается с
расположенной над ней свободной зоной (рис. 5.12, в). Такое перекрытие приводит,
как мы видели, к тому, что обе эти зоны
оказываются укомплектованными лишь частично (рис.5.11).
К первому классу тел относятся, во-первых, химические элементы, атомы которых содержат только заполненные электронные оболочки. В качестве примера рассмотрим неон. В нормальном состоянии распределение электронов в атоме неона следующее: 1s22 s22р6. Все три оболочки атома (1s, 2s, 2р) укомплектованы полностью. В твердом состоянии энергетические уровни 1s, 2s, 2р превращаются в энергетические зоны, способные вместить соответственно 2N, 2N и 6N электронов. Так как N атомов неона содержат 2N электронов 2s, 2N электронов 2s и 6N электронов 2р, то при абсолютном нуле зоны 1s, 2s и 2р окажутся занятыми полностью. Над ними будут располагаться совершенно свободные зоны 3s, Зр и т. д. К первому же классу тел относятся многие химические соединения. В качестве примера рассмотрим кристалл типа NаС1. Атом натрия имеет следующую электронную структуру: 1s22s22р63s1 ; атом хлора — 1s22 s22р6 3s23р5. При образовании молекулы NаС1 один 3s электрон натрия переходит на уровень 3р атома хлора. Образующиеся при этом ионы натрия 1s22 s22р6 и хлора 1s22 s22р63s23р6 ° имеют целиком заполненные электронные оболочки, вследствие чего энергетические зоны кристалла NаС1, возникающие из заполненных атомных уровней, будут укомплектованы полностью. Над ними будут располагаться совершенно свободные зоны.

Ко второму классу твердых тел относятся химические элементы, атомы которых имеют незавершенные оболочки валентных электронов. Рассмотрим, например, натрий, имеющий электронную структуру 1s22 s22р63s1. Внешняя оболочка 3s является у него незавершенной, так как она содержит не 2, а только 1 электрон. В кристалле натрия уровень 3s расщепляется на N подуровней, способных вместить 2N электронов. Вследствие того что N атомов натрия содержат только N электронов 3s, то при абсолютном нуле окажутся заполненными лишь N/2наиболее низких уровней этой зоны, а остальные N/2 уровней останутся свободными. Зона 3s будет заполнена, таким образом, лишь наполовину.
Примерами тел, относящихся к третьему классу, являются химические элементы второй группы таблицы Менделеева. Рассмотрим, например, магний. Он имеет следующую электронную структуру: 1s22 s22р63s2. Все электронные оболочки, в том числе и внешняя 3s, у него укомплектованы полностью. Поэтому магний должен был бы относиться к первому классу тел. Однако вследствие перекрытия зон 3s и 3р каждая из них оказывается заполненной лишь частично
Поведение электронов целиком и частично занятых зон во внешнем поле. Деление тел на изоляторы, проводники и полупроводники.
Согласно зонной теории твердых тел, электроны внешних энергетических зон имеют практически одинаковую свободу движения во всех телах независимо от того, являются эти тела металлами или изоляторами. Оно осуществляется путем туннельного просачивания электронов сквозь потенциальные барьеры, разделяющие соседние атомы кристаллической решетки. В отсутствие внешнего поля это движение не может, однако, привести к возникновению электрического тока, так как распределение электронов по скоростям является симметричным. Это означает, что если в решетке выбрать электрон, движущийся с данной скоростью в данном направлении, то обязательно найдется другой электрон, имеющий скорость такую же по величине, но прямо противоположную по направлению.
Рассмотрим теперь, как ведут себя во внешнем поле электроны целиком заполненных и частично заполненных энергетических зон.
Поведение во внешнем электрическом поле электронов целиком заполненных зон.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.