Электрические свойства твердых тел, страница 7

Для количественного описания процесса поляризации диэлектриков используются величины: поляризованность Р (дипольный момент единицы объема), e - относительная диэлектрическая проницаемость, показывающая, во сколько раз ослабляется напряженность  Е электрического поля в веществе по сравнению с вакуумом. Поскольку e - макроскопическая интегральная характеристика материала, обусловливаемая различными микромеханизмами, при микроскопическом описании используется еще величина a - поляризуемости атомов и молекул. В ряде случаев удобно пользоваться величиной диэлектрической восприимчивости æ, причем æ = e - 1.

При практическом определении величины e часто используют то обстоятельство, что емкость плоского конденсатора, между обкладками которого помещен диэлектрик, в e раз больше, чем емкость того же конденсатора без диэлектрика, т.е. e = С/С₀. Таким образом, экспериментальное определение диэлектрической проницаемости сводится к измерению двух значений электрической емкости, при этом измерения могут производиться как в постоянном, так и в переменных электрических полях.

Полная поляризуемость диэлектрика при участии всех механизмов поляризации, представленных на рис. 2.3.11, описывается суммой:

a = a_э + a_и + a_ор + a_п,                                                        (2.3.18)

где a_э - электронная поляризуемость, a_и - ионная поляризуемость, a_ор - ориентационная поляризуемость, a_п - поляризуемость пространственного заряда.

Для всех видов поляризации и поляризуемых веществ - параэлектриков (кроме сегнетоэлектриков) полагают, что вплоть до сильных полей (E ~ 10⁶ В/м), поляризованность Р  является линейной характеристикой напряженности электрического поля Е.

В частности, поляризованность газа с концентрацией молекул n вследствие электронной поляризованности равна

                                                                (2.3.19)

Было показано, что a_э приблизительно равно R³  - кубу радиуса атома, и не зависит от температуры.

          Если газ состоит из полярных молекул (например, водяной пар), то в не слишком сильных электрических полях (необходимо выполнить условие рЕ<<kT) поляризованность равна

                                                                       (2.3.20)

причем ориентационная поляризованность a_ор обратно пропорциональна температуре и сильно зависит от величины дипольного момента молекул:

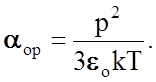                                                                      (2.3.21)

Сохраняется линейный характер зависимости поляризованности от E и при ионной поляризации и поляризации вследствие образования пространственного заряда.

Внутри плотного однородного диэлектрика (твердого тела или жидкости) макроскопическое электрическое поле Е  является суммой

внешнего "наложенного" поля  и внутреннего поля, создаваемого ориентированными диполями. Внутреннее поле характеризуется напряженностью, складывающейся из величины Е₁ напряженности деполяризующего поля связанных зарядов, возникающих на внешних гранях диэлектрика, и напряженностей Е₂ и Е₃, обусловленных локальным взаимодействием зарядов в окрестности рассматриваемой точки диэлектрика. Сумма  представляет собой напряженность макроскопического поля, одинакового во всем объеме образца в виде изотропной плоскопараллельной пластины. Возможное влияние пространственных зарядов учесть весьма сложно из-за неопределенности величины и месторасположения, обусловленного геометрией дефектов образца.

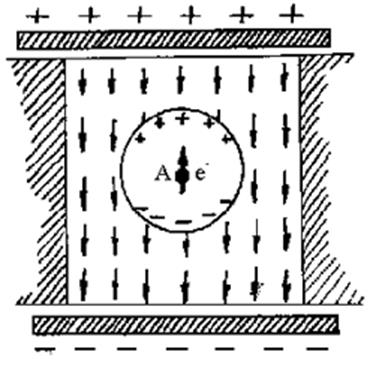
Мысленно вырежем вокруг диполя в точке А небольшую сферу, чтобы можно было точно вычислить параметры поля, создаваемого частицами, окружающими данный диполь (рис.2.3.13). Тогда в каждой точке внутри поверхности сферической полости возникает слой поверхностного заряда противоположного знака. Эти связанные заряды создают в точке А поле ; кроме того, необходимо еще учесть поле , создаваемое удаленными зарядами.

В итоге получим в точке А

                                                        (2.3.22)

Рис.2.3.13. К расчету локального внутреннего поля

Значения  и  удается вычислить для простых кубических решеток и неполярных жидкостей. В этих случаях

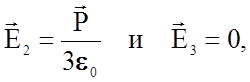                                                         (2.3.23)

где  - интегральная поляризованность объема.

Если А - узел решетки, то напряженность локального поля около него составит

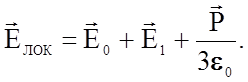                                                         (2.3.24)

Поле Е_лок, определяемое соотношением (2.3.24), называют полем Лорентца. Наведенный этим полем дипольный момент  определяется из условия линейной связи с :

,                                                                        (2.3.25)

здесь a - суммарная поляризуемость, обеспечиваемая всеми возможными для данного диэлектрика механизмами. Тогда поляризованность

в изотропном диэлектрике будет составлять

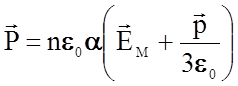,                                                          (2.3.26)

откуда можно найти :

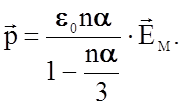                                                                   (2.3.27)

Уравнение (2.3.27) называют формулой Клаузиуса-Моссотти. Часто его представляют в форме

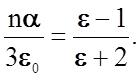                                                                         (2.3.28)

Действительно,

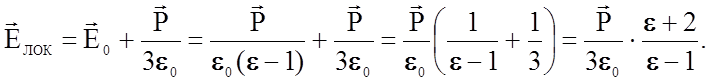
Если теперь учесть связь поляризованности  окрестности рассматриваемой точки А с напряженностью локального поля ,  то получим уравнение (2.3.28).

Уравнение Клаузиуса-Моссотти широко используется в физической химии, но имеет ограниченную применимость при количественном описании керамики  и структур со сложными низкосимметричными решетками; однако для качественных описаний и полуколичественных оценок оно полезно.

Выключение поляризующего внешнего электрического поля приводит к двум видам трансформации внутреннего поля в диэлектрике: быстрой упругой деполяризации вследствие возвращения в исходное состояние электронов и ионов, а также сравнительно медленной релаксации к равновесному хаотическому распределению молекул-диполей и перераспределению объемных зарядов в сторону их компенсации. Упругая поляризация (и деполяризация) у неполярных диэлектриков является единственным видом реакции на не слишком сильное электрическое поле. У материалов, которым свойственна ориентационная поляризация и образование объемных зарядов, она является дополнительной. Постепенное увеличение и уменьшение поляризации вследствие одновременного влияния электрических полей и термических колебаний и диффузии объемных зарядов называется релаксационной поляризацией.