Электрические свойства твердых тел, страница 10

Собственно, прямой пьезоэффект используется для преобразования механических деформаций в электрические сигналы в датчиках давлений и вибраций, микрофонах, адаптерных головных звукоснимателей, датчиках акустической эмиссии и т.п., а обратный пьезоэффект - при изготовлении  ультразвуковых излучателей в широком диапазоне частот. Пьезоэлектрики используются также для стабилизации частоты тока, в качестве фильтров высоких и низких частот.

Пьезоэффект наблюдается во всех кристаллах с нецентросимметричными ячейками. Примерами широко применяемых пьезоэлектриков являются кристаллы KDP(KH₂PO₄) - дигидрофосфат калия, ADP(NH₄H₂PO₄) - дигидрофосфат  аммония, кварц  SO₂, особенно широко применяются пьезокерамики на основе титанатов бария, цирконаты-титанаты свинца (ЦТС)  с общей формулой Рb(ZrТi)O₄, в высокотемпературной области применение находят ниобаты и танталаты лития, калия, натрия (LiNbO₃, LiTiO₃, KTaO₃), метаниобат свинца (Pb_0,6Ba_0,4)Nb₂O₆.

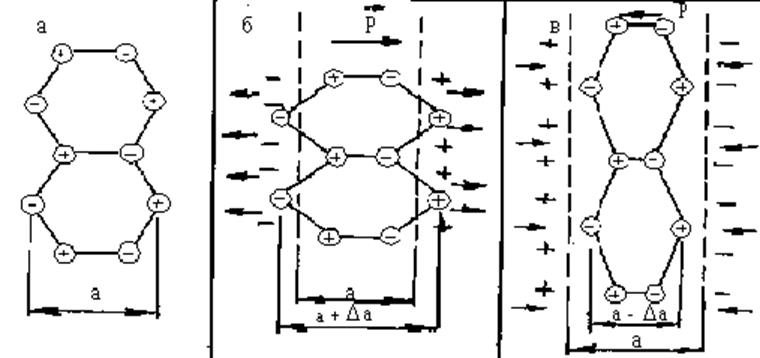
Механизм возникновения поляризации под действием напряжений разного знака пояснен рис.2.3.19 на примере решетки кварца  SiO₂, имеющего гексагональную ячейку с чередованием положительных и отрицательных ионов в узлах. В отсутствие внешнего поля дипольный момент кристаллов кварца, не являющегося сегнетоэлектриком, равен нулю (рис.2.3.19,а). Подвергая кристаллографические ячейки напряжениям растяжения или сжатия (рис.2.3.19,б,в), можно добиться возникновения дипольного момента   различного направления, по величине равного

                                                                       (2.3.32)

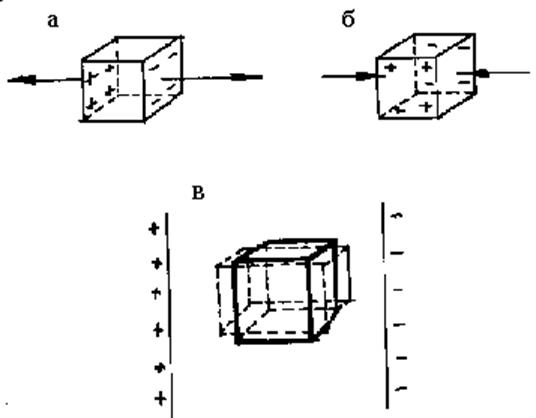Рис. 2.3.18. Прямой (а,б) и обратный (в) пьезоэффект в кристаллах

где Р_i - поляризуемость кристалла в данном направлении i (вообще поляризуемость кристалла  - вектор, описываемый тремя компонентами); s_ik  - тензор напряжений второго ранга с девятью компонентами; d_ijk - тензор пьезоэлектрических модулей (тензор третьего ранга).

Подбирая ориентацию осей при вырезке пьезоэлемента из массивного монокристалла, можно достичь высокой эффективности пьезоустройства при излучении или приеме продольных или поперечных волн, что особенно характерно при использовании кварца. Если в качестве пьезоэлемента используется поликристаллическая керамика, изготовленная методами горячего прессования или литья под давлением, то поляризованность можно считать связанной с механическими напряжениями соотношением вида (2.3.32), то есть  Р=d×s, но обычно рассматривают напряжения и деформации лишь вдоль  двух осей - продольной и поперечной относительно направления деформирования

Рис.2.3.19. Возникновение и изменение пьезополяризации в кварце: а  - деформация отсутствует, б – под действием напряжений растяжения; в - под действием напряжений сжатия

В случае цилиндрического пьезоэлектрического образца, деформируемого вдоль оси цилиндра, рассматривают продольную и радиальную деформации. Соответственно различают для пьезокерамики продольный d₃₃ и радиальный d₃₁ пьезомодули. Поскольку величина пьезомодулей сильно зависит от частоты воздействия деформирующего поля, в таблицах обычно приводят лишь характеристики для статических полей. В частности, для широко применяемого титаната бария значения пьезомодулей колеблются около значений:

d₃₃ = (4…6)×10^-6 см/(ст.В), d₃₁ =(2…2,5)×10^-6 см/(ст.В).

Среднее значение d₃₁ распространенных видов пьезокерамики ЦTC можно считать равным (4,12…4,65)×10^-6 см/(ст.В); ст.В – напряжение статического поля в вольтах.

При проектировании ультразвуковых излучателей часто используется также коэффициент электромеханической связи K_p, характеризующий способность пьезоэлектрика к трансформации механической энергии в электрическую. Для BaTiO₃ K_p составляет 0,18…0,37, для керамики ЦТС  К_р =0,43…0,52, но вообще К_р, этот своеобразный КПД пьезоэлектрика, может достигать 0,8.

Пьезоэлектрические свойства кристаллов с изменением температуры могут как улучшаться, так и ухудшаться, но при достижении температуры Кюри Т_с они исчезают. Пьезоэлектричество не следует смешивать с электрострикцией - способностью любого диэлектрического тела к изменению размеров под действием электрического поля из-за ионной и ориентационной поляризации.

2.3.6. Диэлектрики в переменных электрических полях

Вообще поляризуемость диэлектрика в электрическом поле – обратимый процесс, однако полный цикл "поляризация - деполяризация" требует тем большего времени, чем больше механизмов поляризации задействовано, чем больше время релаксации (ф.2.3.31). Ускорение релаксации, а также изменения направления поляризации диэлектрика в электрических полях переменного направления требуют потерь энергии источника поля. В конечном итоге эта энергия превращается в теплоту, суммирующуюся с ленц-джоулевой теплотой, выделяющейся в диэлектрике, как и в любом веществе, при пропускании по нему тока. Токи проводимости (или сквозные токи) в диэлектриках невелики, но пренебрегать ими  нельзя.

Рис.2.3.20. Изменение электрической индукции D в диэлектрике в переменном электрическом поле Е: а - запаздывание и потери отсутствуют, б - при наличии потерь

Представим себе пластину из диэлектрика, помещенную в поле плоского конденсатора, к пластинам которого приложено электрическое поле, изменяющееся во времени по синусоидальному закону:

                                                                    (2.3.33)

где w - круговая частота поля. Плотность j_å суммарного тока, который при этом будет течь через диэлектрик, складывается из плотности тока проводимости и плотности тока смещения

j_å = j_пр + j_см,

где

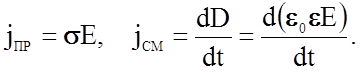
Если бы перестройка структуры во внешнем электрическом поле происходила мгновенно, то электростатическая индукция D  изменялась бы синфазно с внешним полем Е по уравнению

                                                                      (2.3.34)

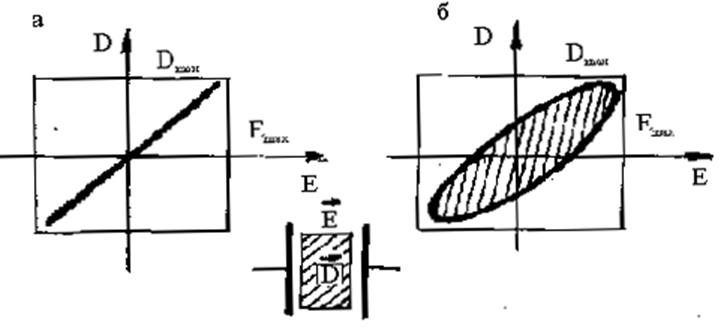
и имел бы место случай, представленный на рис.2.3.20,а.

Однако в результате запаздывания поляризации электрическая индукция D  будет изменяться не в фазе с полем  Е.  Для количественного описания этого процесса диэлектрическую проницаемость e  в переменных электрических полях представляют в виде комплексной функции частоты:

          e(w) = e¢(w) - ie¢(w).                                                            (2.3.35)