Спектральные представления непериодических сигналов. Вариант 9

Новосибирский Государственный Технический Университет

Факультет Автоматики и Вычислительной Техники

Кафедра  ССОД

Дисциплина  «Теория  и  обработка  сигналов»

Лабораторная работа № 3

СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ

НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ

ВАРИАНТ №9

Выполнила:                                                                                                  Проверил:

Баранова К.В.                                                                                              доц. Щетинин Ю.И.

Группа: АО-61

Новосибирск, 2008

Цель работы:Изучение преобразования Фурье и его свойств, понятий амплитудного и фазового спектров непериодических непрерывных во времени сигналов, приобретение практических навыков вычисления преобразования Фурье и построения графиков и анализа спектров в среде Matlab.

            Условия:

 

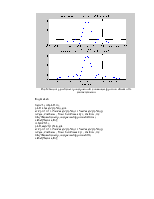
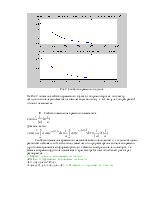
Рис.1. График заданного сигнала.

           

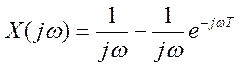
1.  Аналитическое  определение прямого преобразования Фурье для заданного сигнала (Рис.1).

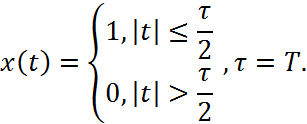
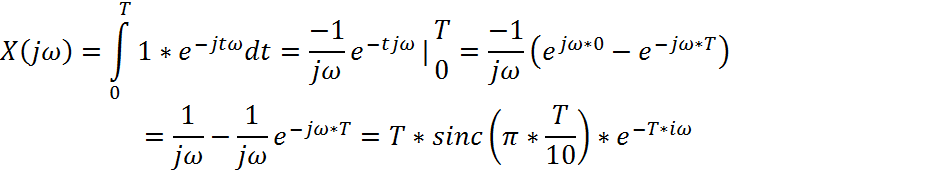
2.  Построение графиков амплитудного и фазового спектров.

Код MatLab:

T=10;

f=0:0.01:T;

 w=2*pi*f;

x=1./(i.*w)-1./(i.*w).*exp(-i.*w*10); % выражение комплексного спектра

subplot(311), plot(f,abs(x)); axis([0,1,0,10]);

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Амплитудный спектр')

subplot(312), plot(f,unwrap(angle(x)));axis([0,1,-4,0])

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Фазовый спектр');

subplot(313);                        

t =0: 1/1000:10;A=1; tau=10;x=A*rectpuls(t-tau/2,tau);%выражение для построения графика

 plot(t,x)  % заданного сигнала

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title(‘Заданный cигнал’);

  

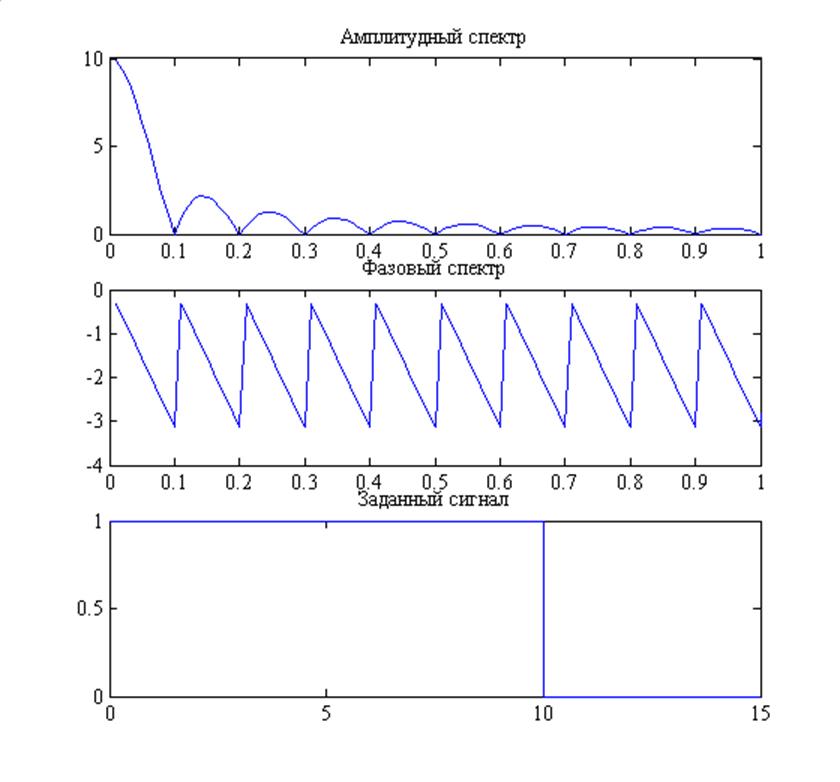
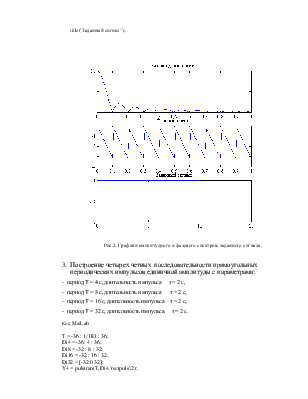
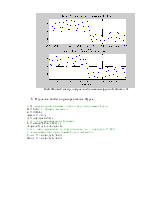
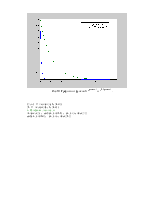
Рис.2. Графики амплитудного и фазового спектров, заданного сигнала.

3.  Построение четырех четных  последовательности прямоугольных периодических импульсов единичной амплитуды с параметрами:

-  период Т = 4 с, длительность импульса  τ = 2 с,

-  период Т = 8 с, длительность импульса   τ = 2 с,

-  период Т = 16 с, длительность импульса τ = 2 с,

-  период Т = 32 с, длительность импульса  τ = 2 с.

Код MatLab:

T = -36 : 1/1E1 : 36;

Di4 = -36: 4 : 36;

Di8 = -32 : 8 : 32;

Di16 = -32 : 16 : 32;

Di32 = [-32 0 32];

Y4 = pulstran(T,Di4,'rectpuls',2);

Y8 = pulstran(T,Di8,'rectpuls',2);

Y16 = pulstran(T,Di16,'rectpuls',2);

Y32 = pulstran(T,Di32,'rectpuls',2);

subplot(4,1,1); plot(T,Y4); axis([min(T) max(T) 1.1*min(Y4) 1.1*max(Y4)]);

title('Прямоугольный cигнал   T=4,8,16,32');

subplot(4,1,2); plot(T,Y8); axis([min(T) max(T) 1.1*min(Y8) 1.1*max(Y8)]);

subplot(4,1,3); plot(T,Y16); axis([min(T) max(T) 1.1*min(Y16) 1.1*max(Y16)]);

subplot(4,1,4); plot(T,Y32); axis([min(T) max(T) 1.1*min(Y32) 1.1*max(Y32)]);

xlabel('t, sec');

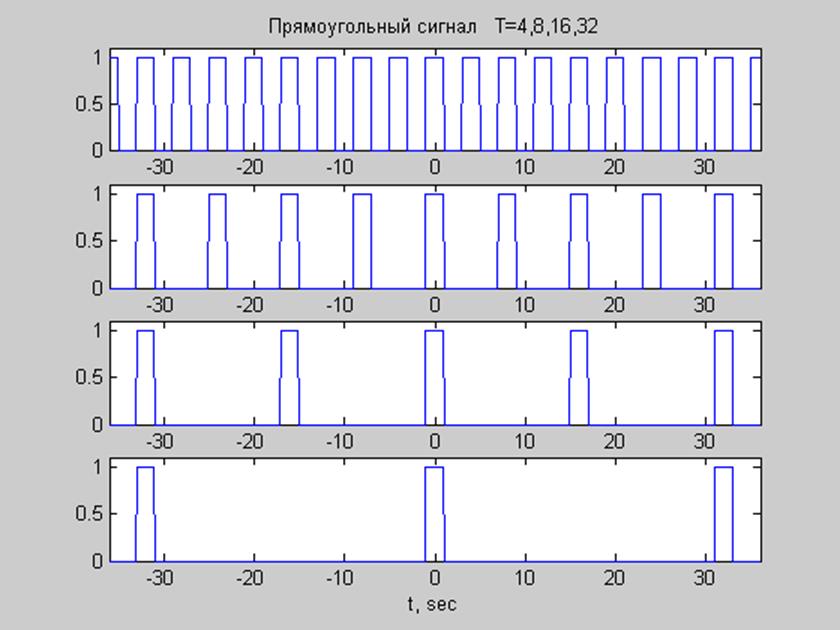
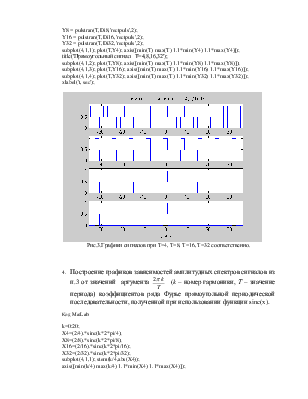
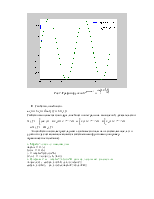
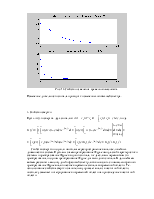
                  Рис.3.Графики сигналов при T=4, T=8, T=16, T=32 соответственно.

4.  Построение графиков зависимостей амплитудных спектров сигналов из п.3 от значений  аргумента 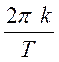  (k – номер гармоники, Т – значение периода) коэффициентов ряда Фурье прямоугольной периодической последовательности, полученной при использовании функции sinc(x).

Код MatLab:

k=0:20;

X4=(2/4).*sinc(k*2*pi/4);

X8=(2/8).*sinc(k*2*pi/8);

X16=(2/16).*sinc(k*2*pi/16);

X32=(2/32).*sinc(k*2*pi/32);

subplot(4,1,1); stem(k/4,abs(X4));

axis([min(k/4) max(k/4) 1.1*min(X4) 1.1*max(X4)]);

title(' Амплитудные cпектры ')

subplot(4,1,2); stem(k/8,abs(X8));

axis([min(k/8) max(k/8) 1.1*min(X8) 1.1*max(X8)]);

subplot(4,1,3); stem(k/16,abs(X16));

axis([min(k/16) max(k/16) 1.1*min(X16) 1.1*max(X16)]);

subplot(4,1,4); stem(k/32,abs(X32));

axis([min(k/32) max(k/32) 1.1*min(X32) 1.1*max(X32)]);

xlabel('Чаcтота, Hz');

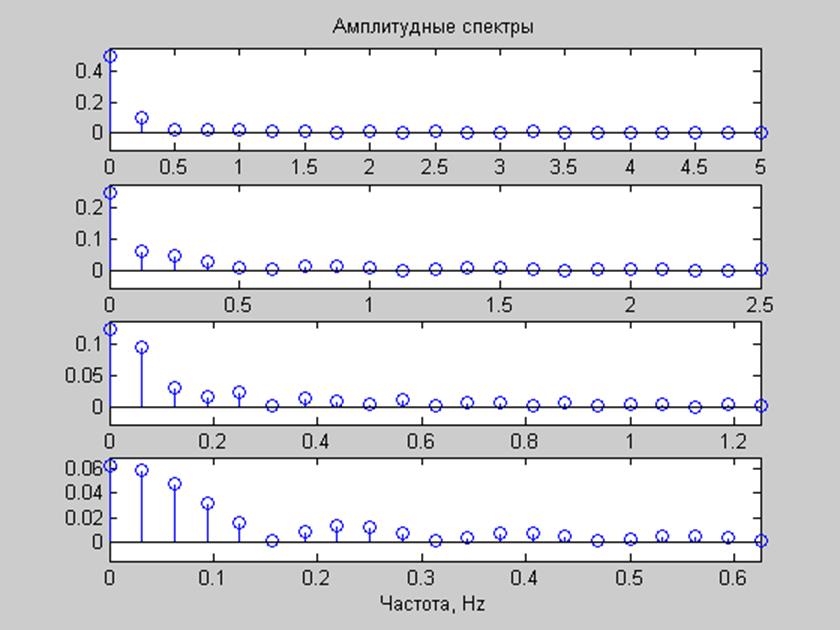
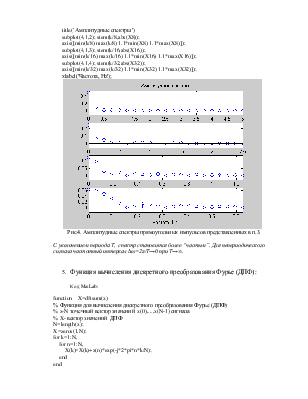
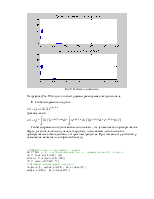
Рис.4. Амплитудные спектры прямоугольных импульсов представленных в п.3.

С увеличением периода T,  спектр становится более “частым”. Для непериодического сигнала частотный интервал ∆ω=2π/T→0 при T→∞.

5.  Функция вычисления дискретного преобразования Фурье (ДПФ):

Код MatLab:

function    X=dftsum(x)

% Функция для вычисления дискретного преобразования Фурье (ДПФ)

% x-N точечный вектор значений  x(0),...,x(N-1) сигнала

% X- вектор значений  ДПФ

N=length(x);

X=zeros(1,N);

for k=1:N,

    for n=1:N,

        X(k)=X(k)+x(n)*exp(-j*2*pi*n*k/N);

    end

end

6.  Вычисление с помощью функции dftsum(x) (см.п.5)  ДПФ сигнала, заданного в п.1, и построение графиков его амплитудного и фазового спектров.

Код MatLab:

T=10;

dt=0.05; % интервал отсчетов

t=0:dt:T; % задание интервала времени

A=1; s1= A*rectpuls(t-T/2,T);% задание сигнала

% дополнение сигнала нулями для увеличения частотного разрешения df

s=[3*zeros(1, length(t)-1) s1 3*zeros(1, length(t)-1)];

y1p=fftshift(dftsum(s));

Fmax=1/dt;

df=1/(dt*length(s));

f=-Fmax/2+df/2:df:Fmax/2-df/2;

figure(1), subplot(211),

plot(f+df,abs(y1p*dt)), grid

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,10);

title('Амплитудный спектр, построенный функцией dftsum')

xlabel('Частота, Гц');

axis([-0.5 0.5 0 1.1*max(abs(y1p*dt))]);

subplot(212);

plot(f+df,angle(y1p*dt)), grid

axis([-0.5 0.5 1.1*min(angle(y1p*dt)) 1.1*max(angle(y1p*dt))]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,10);

title('Фазовый спектр, построенный функцией dftsum')

xlabel('Частота, Гц');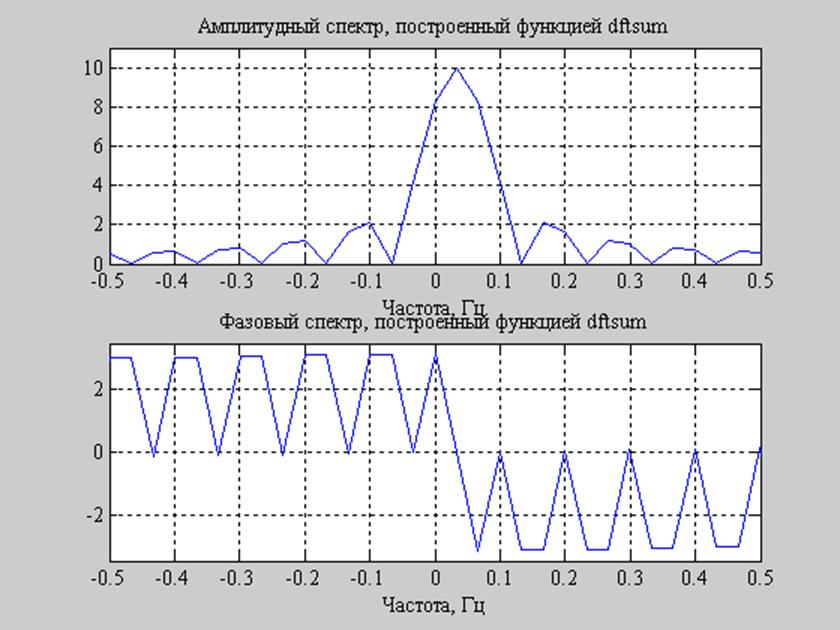

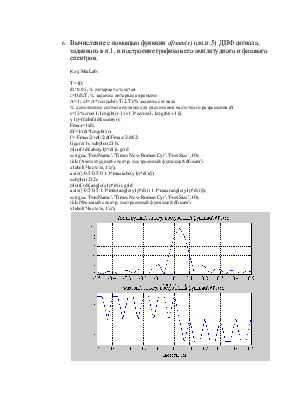
Рис.5. Амплитудный и фазовый спектры заданного сигнала, построенные с помощью функции dftsum().

7.  Сравнение амплитудного и фазового спектров заданного сигнала, построенных с помощью функции: