Спектральные представления непериодических сигналов. Вариант 9, страница 2

- fft()

- dftsum()

Код MatLab:

T=10;

dt=0.05; % интервал отсчетов

t=-T:dt:T; % задание интервала времени

A=1; s1= A*rectpuls(t-T/2,T);% задание сигнала

% дополнение сигнала нулями для увеличения частотного разрешения df

s=[3*zeros(1, length(t)-1) s1 3*zeros(1, length(t)-1)];

fy1p=fftshift(fft(s));

y1p=fftshift(dftsum(s));

Fmax=1/dt;

df=1/(dt*length(s));

f=-Fmax/2+df/2:df:Fmax/2-df/2;

figure(1), subplot(211),

plot(f+df,abs(y1p*dt)), grid

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,10);

title('Амплитудный спектр, построенный функцией dftsum')

xlabel('Частота, Гц');

axis([-0.5 0.5 0 1.1*max(abs(y1p*dt))]);

subplot(212),

plot(f,abs(fy1p*dt)), grid

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,10);

 title('Амплитудный спектр, построенный функцией fft')

xlabel('Частота, Гц');

axis([-0.5 0.5 0 1.1*max(abs(y1p*dt))]);

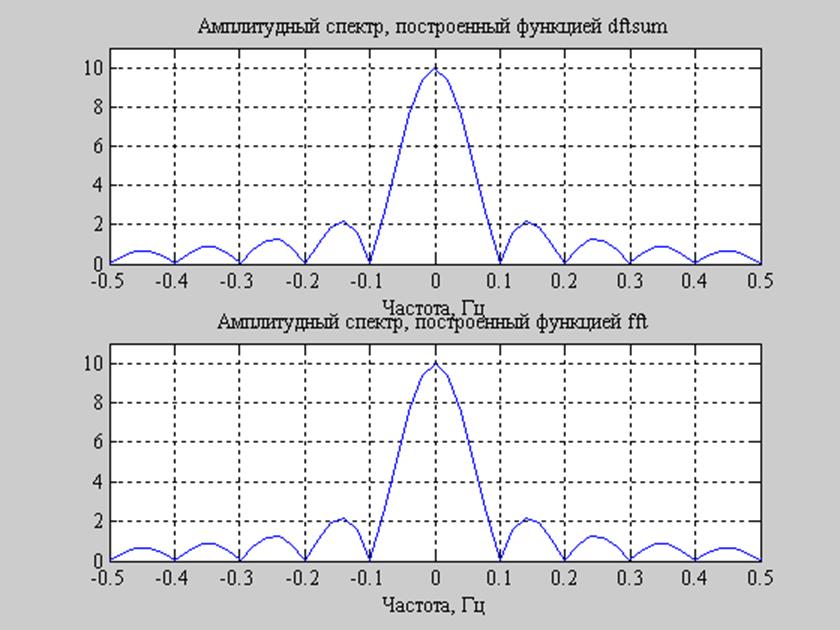
Рис.6. Амплитудный спектр построенный с помощью функции dftsum и fft, соответственно.

Код MatLab:

figure(2), subplot(211),

plot(f+df,angle(y1p*dt)), grid

axis([-0.5 0.5 1.1*min(angle(y1p*dt)) 1.1*max(angle(y1p*dt))]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,10);

title('Фазовый спектр, построенный функцией dftsum')

xlabel('Частота, Гц');

subplot(212),

plot(f,angle(fy1p*dt)),grid

axis([-0.5 0.5 1.1*min(angle(y1p*dt)) 1.1*max(angle(y1p*dt))]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,10);

title('Фазовый спектр, построенный функцией fft')

xlabel('Частота, Гц');

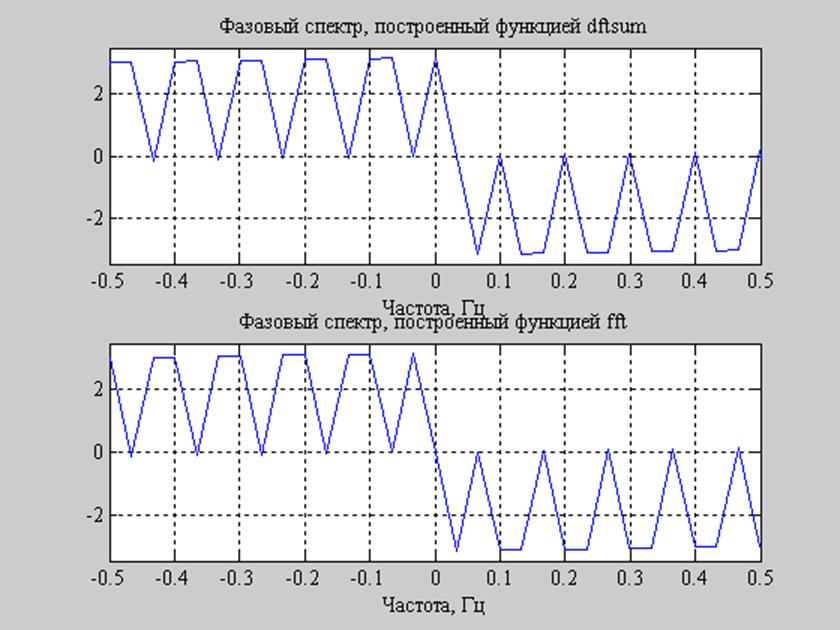
Рис.6. Фазовый спектр, построенный с помощью функций dftsum и fft.

8.  Изучение свойств преобразования Фурье.

% Процедура иллюстрации свойств преобразования Фурье

N = 128; %  Длина сигналов

k = 0:N-1;

gamma = -0.5;

g = exp(gamma*k);

% g - экспоненциальная функция

h = sin(2*pi*k/(N/2));

figure(1),plot(k,g,k,h)

% h - синусоидальная последовательность с периодом = N/2

% вычисление преобразований Фурье сигналов

[G,w] = freqz(g,1,512);

[H,w] = freqz(h,1,512);

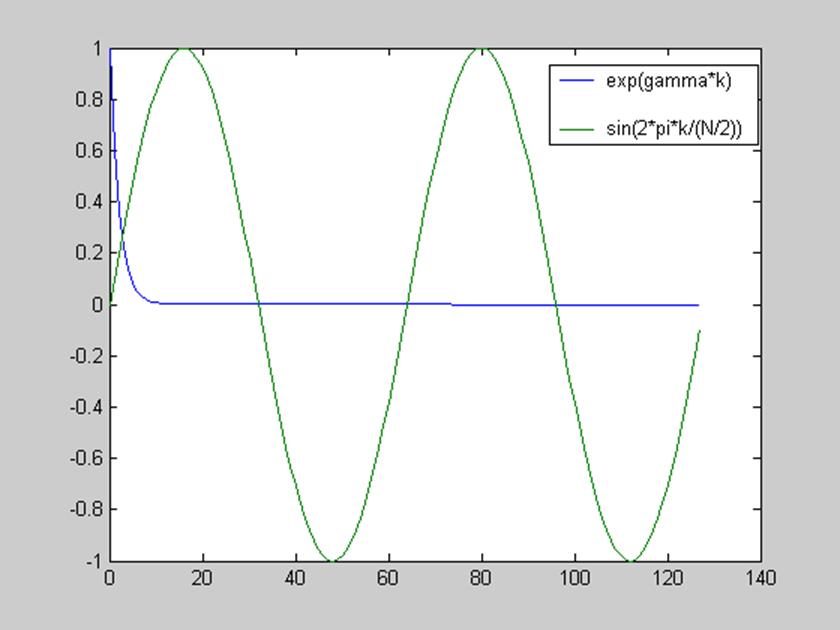
Рис.7. Графики функций  и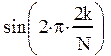

v  Свойство линейности.

Свойство выполняется благодаря линейности интегральных вычислений, доказательство:

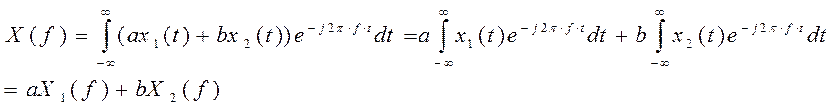
      Это свойство позволяет раскладывать сложные сигналы на их составляющие, а это удобно когда составляющие являются собственными функциями (например, гармонические колебания).

% М-файл Свойство линейности

alpha = 0.5;

beta = 0.25;

y = alpha*g+beta*h;

[Y,w] = freqz(y,1,512);

% Графики Y и  alpha*G+beta*H для проверки их равенства

figure(2), subplot(211),plot(abs(Y))

subplot(212), plot(abs(alpha*G+beta*H))

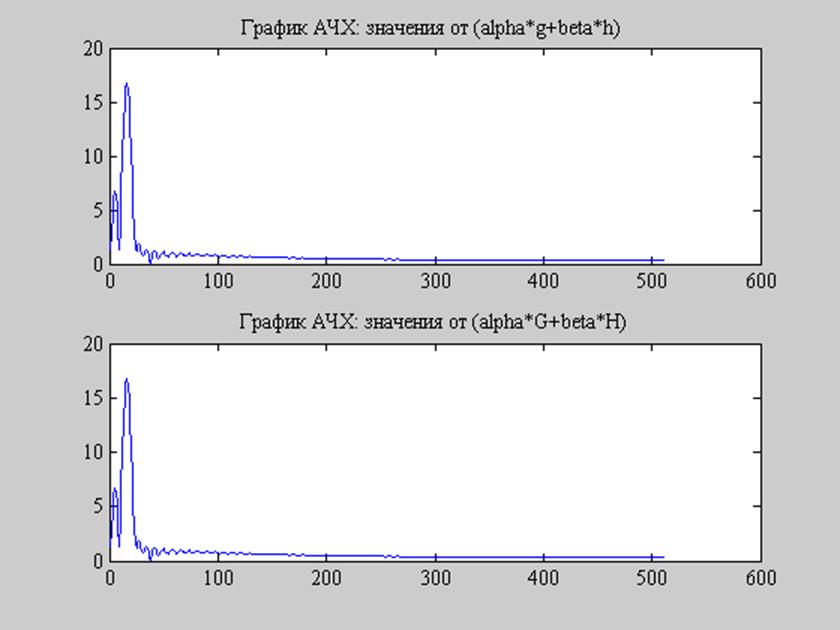
Рис.8. Свойство линейности.

На графике (Рис. 10) видно, что спектр суммы равен сумме спектров сигнала.

v  Свойство временного сдвига

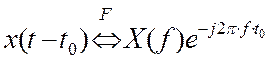
Доказательство: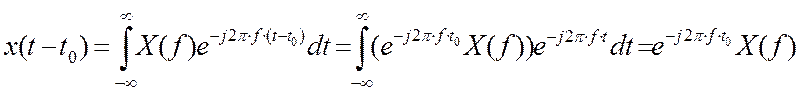

      Свойство временного сдвига можно использовать,  когда нам известно преобразование Фурье для сигнала (обычно у начала координат), то мы можем  легко вычислить преобразование с теми сдвигами,  которые нам требуются. При этом амплитудный спектр не меняется, меняется только фазовый спектр.

% М-файл Свойство временного сдвига

n0 = 12; % y2 - последовательность y, сдвинутая на 12 отсчетов

y2 = [zeros([1,n0]) g];

[Y2,w] = freqz(y2,1,512);

G0 = exp(-j*w*n0).*G;

% Графики амплитудных спектров

figure(3), subplot(211), plot(abs(G0))

subplot(212), plot(abs(Y2));

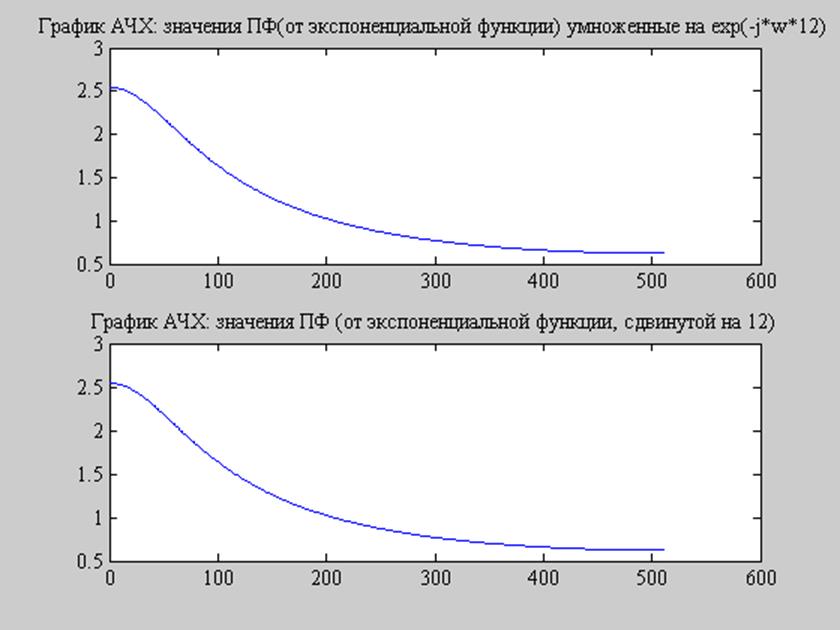
Рис.9. Свойство временного сдвига.

На Рис. 9 показано свойство временного сдвига в котором говорится, что спектр исходного сигнала умножается на комплексную величину , модуль которой равен 1 и значит не меняется.

v  Свойство изменения временного масштаба

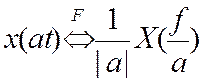
Доказательство:

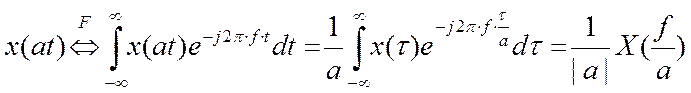
Свойство изменения временного масштаба можно использовать,  когда необходимо  растягивать/сжимать кой либо сигнал, заметим, что при расширение сигнала во времени (при этом сохраняется его форма) приводит к сжатию спектра сигнала и наоборот, т.е. сжатая во времени функция изменяется в а раз быстрей, а частотный спектр ее в а раз расширяется.

% М-файл Свойство изменения масштаба

a=0.1;% Коэффициент изменения масштаба

g1= exp(gamma*k*a);

figure(4),plot(k,g,k,g1) % Графики во временной области

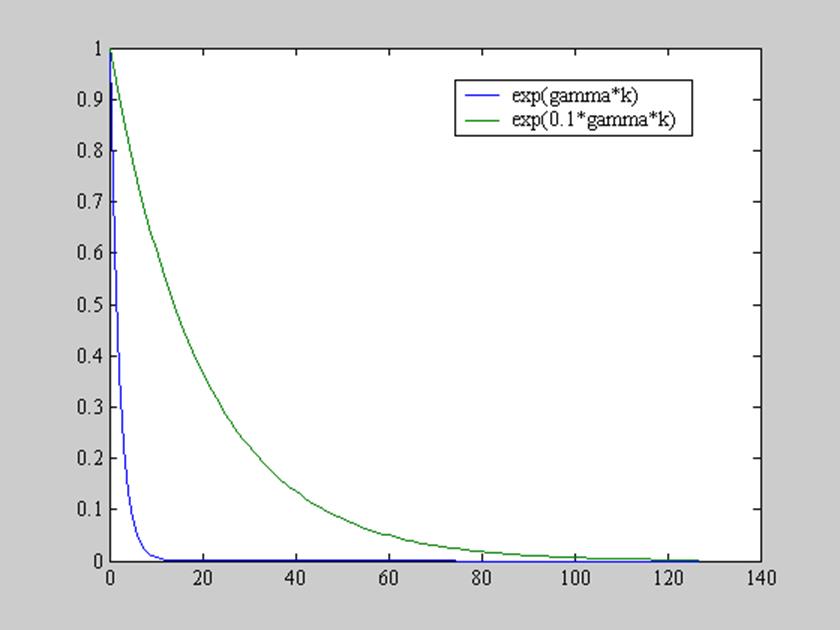
Рис.10. Графики от функций   и .

[G,w] = freqz(g,1,512);

G1 = freqz(g1,1,512);

% Графики спектров

figure(5), subplot(211), plot(w,abs(G))

subplot(212), plot(w,abs(G1))

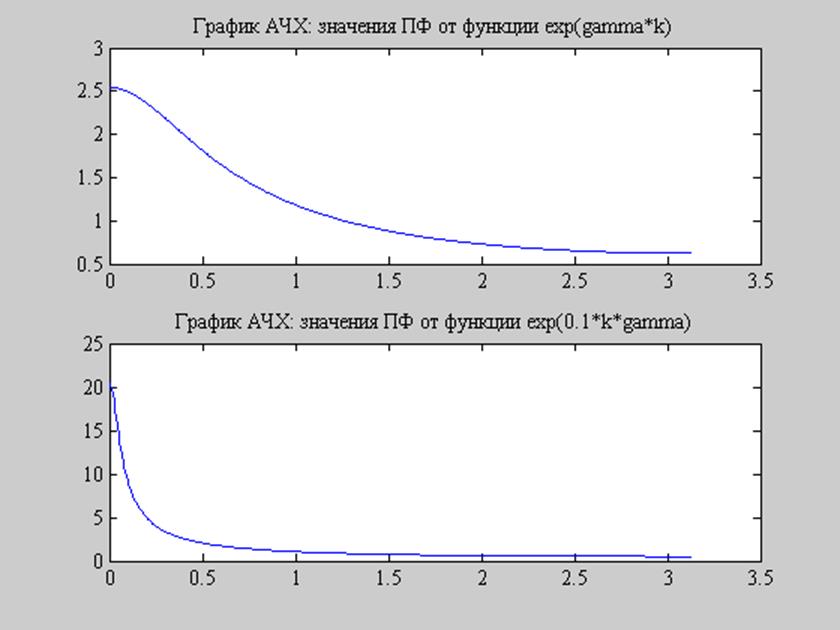
Рис. 13 Свойство изменения временного масштаба

Изменение длительности сигнала приводит к изменению огибающей спектра.

4. Свойство свертки

Пусть x(t) это свертка  двух сигналов: 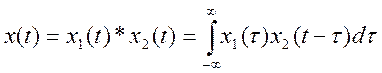, тогда

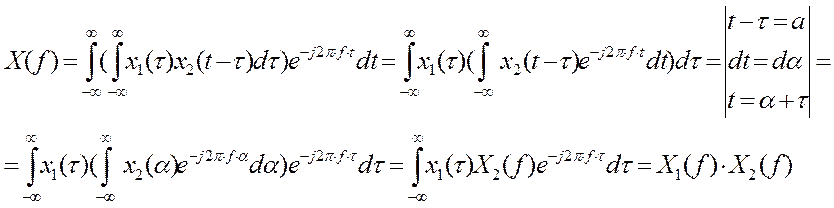
      Свойство свертки получило наибольшее распространение в анализе линейных динамических систем. Пусть мы знаем преобразование Фурье импульсной характеристики системы и преобразование Фурье входного сигнала, тогда если мы перемножим эти преобразования, получим преобразование Фурье для выходного сигнала. В дальнейшем можем рассчитать амплитудный и фазовый спектр либо вычислить с помощью обратного преобразование Фурье аналитическое выражение сигнала во временной области. Т.е. использование свойства свертки значительно упрощает анализ в частотной области, поскольку заменяет интегрирование во временной области на произведение в частотной области.

% М-файл Свойство свертки

y5 = conv(g,h);

[Y5,w] = freqz(y5,1,512);

figure(6), subplot(211), plot(abs(Y5))

subplot(212), plot(abs(G.*H))

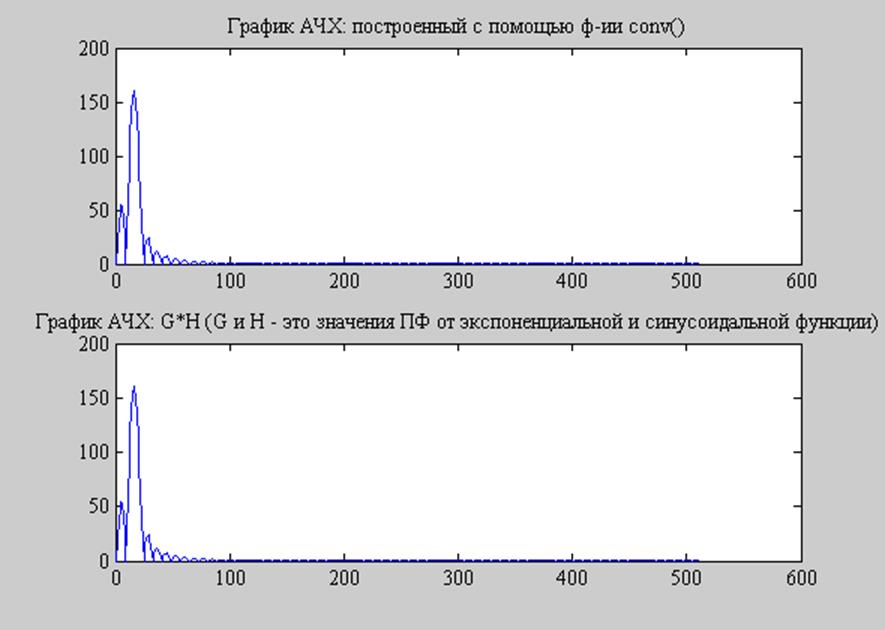
Рис. 14 Свойство свертки

Спектр свертки равен произведению спектров сигналов.

% М-файл Теорема Парсеваля

val1 = sum(g.*conj(h));

val2 = sum(G0.*conj(H))/512;

% Сравнение val1 с val2

disp('Разность   val1-val2 = '),disp(val1-val2)

Результат:

Разность   val1-val2 =

  -2.0510 - 0.1066i