Спектральные представления непериодических сигналов. Вариант 7

            МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ 
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

ЛАБОРАТОРНАЯ  РАБОТА  № 3

СПЕКТРАЛЬНЫЕ  ПРЕДСТАВЛЕНИЯ

НЕПЕРИОДИЧЕСКИХ  СИГНАЛОВ

Вариант 7

Группа: АТ-73                                                                             Преподаватель: доц. Щетинин Ю.И.

Студент: Кухарева А.В.

Новосибирск

 2009

Цель работы:  изучение преобразования Фурье и его свойств, понятий амплитудного и фазового спектров непериодических непрерывных во времени сигналов, приобретение практических навыков вычисления преобразования Фурье,  построения графиков и анализа спектров в среде Matlab.

1.  Изучение связи между спектрами периодического и непериодического сигналов.

Определим коэффициенты комплексного ряда Фурье прямоугольной периодической последовательности с периодом Т₀, длительностью импульсов τ и амплитудой U (рис. 1).

Рис. 1. График прямоугольной периодической последовательности.

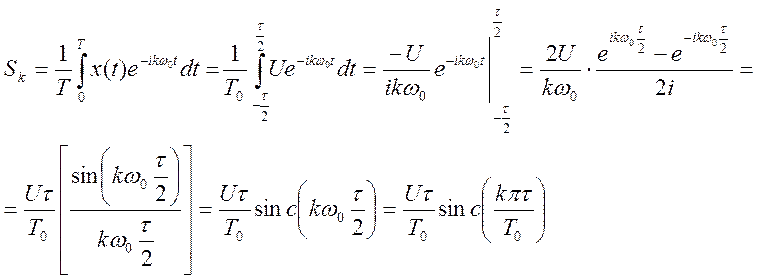                            (1)

В выражении (1) .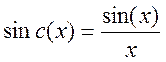

Ряд  Фурье в комплексной форме будет иметь вид 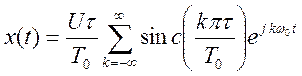(2).

.                                                                                  (2)

С помощью следующего script-файла сформируем четыре четные  последовательности прямоугольных периодических импульсов единичной амплитуды с параметрами:

     а)  период Т = 1 с, длительность импульса τ = 0.25 с,

     б) период Т = 4 с, длительность импульса τ = 0.25 с,

     в) период Т = 8 с, длительность импульса τ = 0.25 с,

     г) период Т = 32 с, длительность импульса τ = 0.25 с.

tau = 0.25;

T = [1 4 8 32];

N = 35; % число импульсов

t = -33:0.001:33;

for n = 1:4,

d = 0:T(n):(N-1)*T(n); % вектор задержек для pulstran

s = pulstran(t, d, 'rectpuls', tau); % последовательность из N импульсов

d = -(N-1)*T(n):T(n):-1; % отрицательные номера

s = s + pulstran(t, d, 'rectpuls', tau);

subplot(4,1,n)

plot(t,s)

title(['T = ',num2str(T(n))])

end

Графики, полученные в результате выполнения script-файла, приведены на рис. 2.

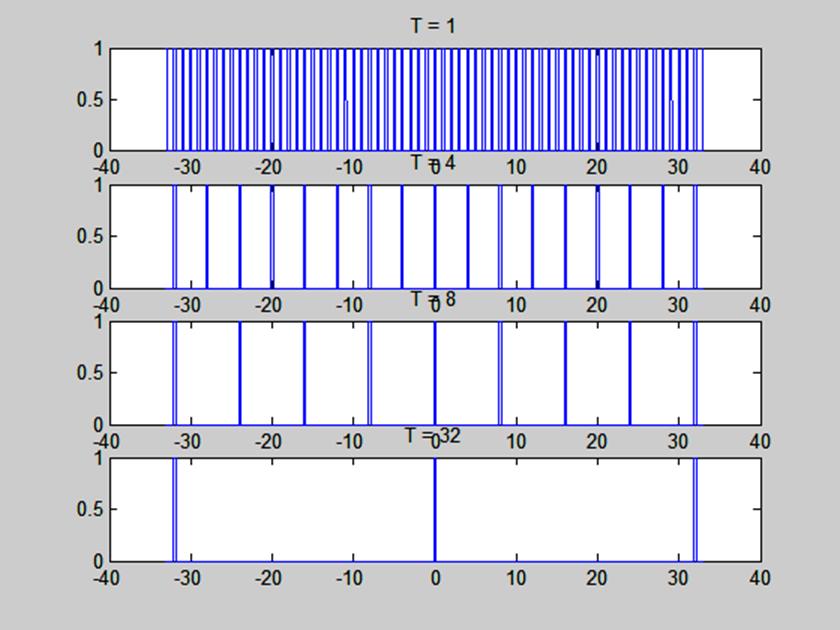
Рис. 2. Графики прямоугольных периодических импульсов с периодом T.

С помощью следующего script-файла построим графики зависимостей амплитудных спектров данных сигналов от значений  аргумента .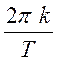

tau = 0.25;

T = [1 4 8 32];

k=-20:20;

for n = 1:4,

ck=(tau/T(n))*sinc(k*tau/T(n));

subplot(2,2,n), stem(2*k*pi/T(n),abs(ck))

title(['T = ',num2str(T(n))])

end

Полученный результат  представлен на рис. 3.

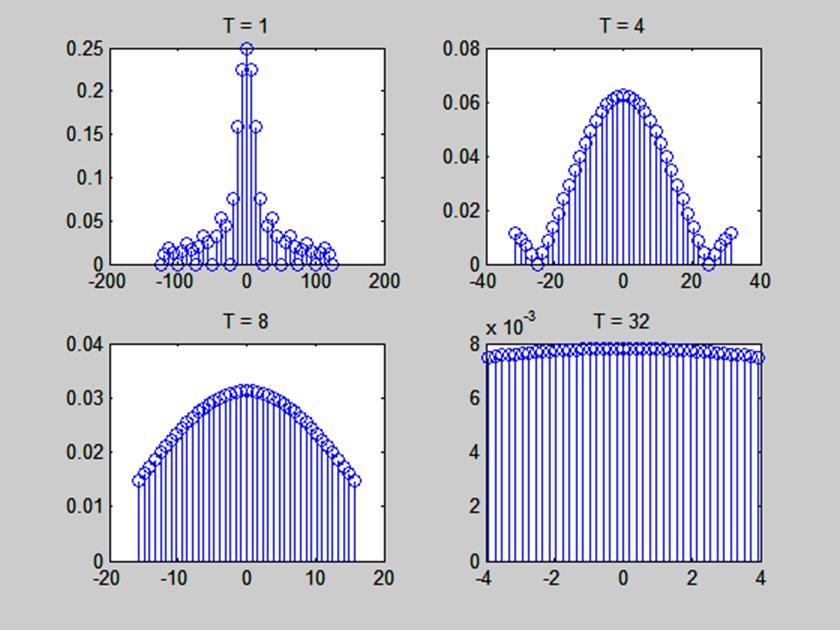
Рис. 3. Амплитудные спектры прямоугольных периодических импульсов с периодом Т.

сдесь должно быть разное кол-во гармоник на разных графиках, чтобы было видно, что спектр чаще

Видим, что при увеличении периода спектр становится более «частым».

На основании этого делаем вывод, что при  плотность линий спектра увеличивается и спектр становится сплошным.

Для непериодических сигналов можно считать, что , значит, спектр непериодического сигнала также будет сплошным.

Таким образом, различие между спектрами периодического и непериодического сигналов в том, что спектр периодических сигналов – линейчатый, а непериодических – сплошной. Спектр непериодического сигнала можно получить из периодического путём предельного перехода при .

2.   Определение прямого преобразования Фурье сигнала и построение графиков его амплитудного и фазового спектров.

Дан двусторонний экспоненциальный сигнал вида .        

Найдём прямое преообазование Фурье сигнала .

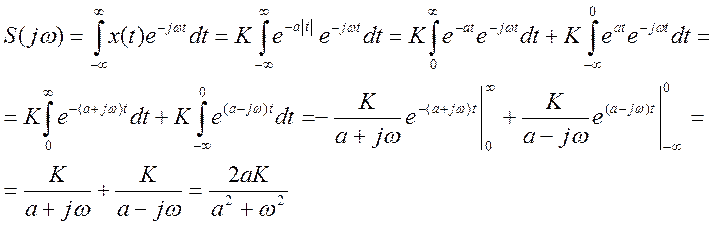                                             (3)

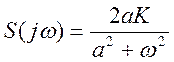Таким образом, спектральная плотность для сигнала  будет иметь вид (4).

                                                                                                                             (4)

С помощью следующего script-файла построим графики сигнала и его амплитудного и фазового спектров.

T=10;

dt=0.1; % задание интервала отсчетов

t=-T:dt:T;   % длительность сигнала

K=5; a=5;

s=K*exp(-a*abs(t)); % определение сигнала

df=1/(9*T); Fmax=1/dt; % задание частотной шкалы

f=-Fmax:df:Fmax;

omega = 2*pi*f;

S=2*a*K./(a^2 + omega.^2); % выражение комплексного спектра

% построение графиков сигнала и спектров

subplot(311), plot(t,s)

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Cигнал')

subplot(312), plot(f,abs(S))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Амплитудный спектр')

subplot(313), plot(f,angle(S))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Фазовый спектр')

Полученный результат представлен на рис. 4.

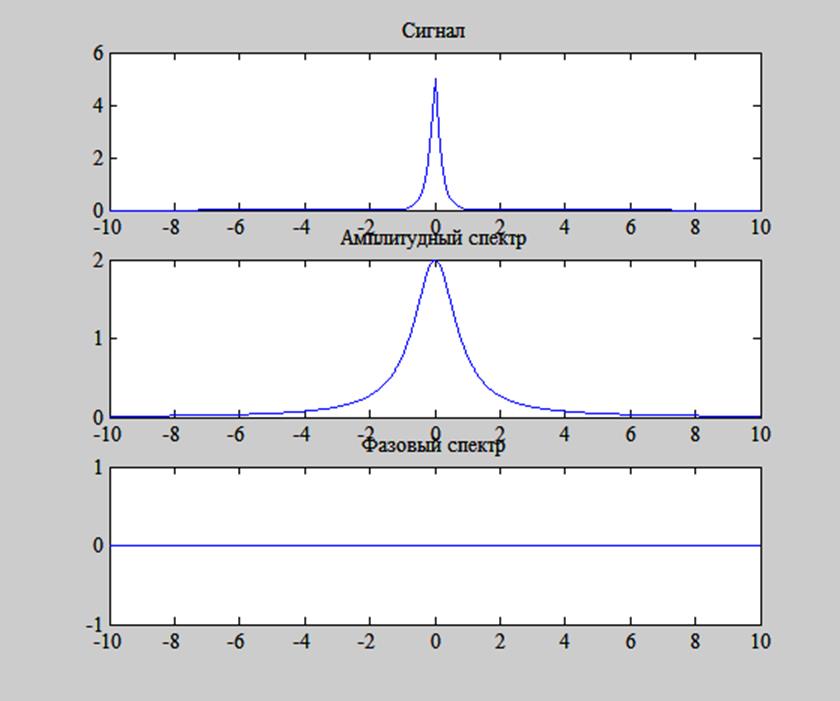
Рис. 4. График сигнала x(t) и его амплитудного и фазового спектров.

Фазовый спектр сигнала нулевой, т.к. сигнал чётный и .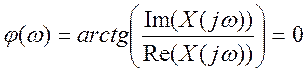

3.   Вычисление дискретного преобразования Фурье сигнала и построение графиков его спектров.

Функция вычисляет дисктретное преобразование Фурье сигнала и имеет вид:

function X = dftsum(x)

% вычисляет дискретное преобразование Фурье

% x вектор значений x(0),...,x(N-1)сигнала, X-вектор значений ДПФ

N = length(x);

k = 0:(N-1);

for n = 0:(N-1),

    s = x(k+1).*exp(-i*2*pi*k*n/N);

    X(n+1) = sum(s);

end

Воспользовавшись функцией , найдём амплитудный и фазовый спектры сигнала и построим их графики.

Следующий script-файл выполняет эту задачу.

% Вычисление спектра и построение его графиков

T=10; dt=0.1; % Определение интервала времени

dt сделать таким, чтобы график был пореже, точками, а не одной линией

t=-T:dt:T;

K=5; a=5;

s=K*exp(-a*abs(t));  % задание сигнала

% Добавление нулей к сигналу для увеличения частотного разрешения

S=[zeros(1,2*length(t))  s  zeros(1,2*length(t))];

df=1/(dt*length(S)); Fmax=1/dt;   % определение частотной шкалы

f=-(Fmax-df):2*df:Fmax;

y1=dftsum(S); y1p=fftshift(y1);    % вычисление и сдвиг ДПФ

% Построение графиков сигнала и его спектров

subplot(3,1,1), plot(t,s)

set(gca,'FontName','Arial Cyr', 'FontSize',12)

title('Сигнал')

subplot(3,1,2), plot(f,abs(y1p)*dt,'o-')

set(gca,'FontName','Arial Cyr', 'FontSize',12)

title('Амлитудный спектр'),grid

subplot(3,1,3), plot(f,angle(y1p)),

set(gca,'FontName','Arial Cyr', 'FontSize',12)

title('Фазовый спектр')

xlabel('Частота,  Гц'), grid

Полученный результат представлен на рис. 5.

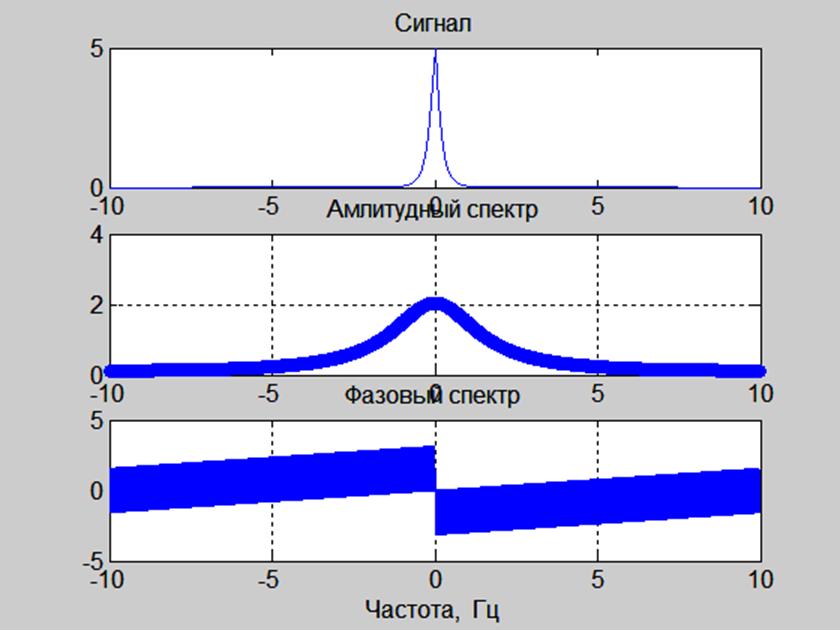
Рис. 5. График сигнала и его спектров, вычисленных с помощью ДПФ.

4.   Сравнение спектров, полученных с помощью НВПФ, ДПФ и функции fft(t).

С помощью следующего script-файла построим графики амплитудных спектров сигнала, применяя преобразование Фурье непрерывного времени (НВПФ), дискретное преобразование Фурье (ДПФ) и функцию fft(), реализующую алгоритм быстрого преобразования Фурье.

T=10; dt=0.1; % Определение интервала времени

t=-T:dt:T;

K = 5; a=5;

s=K*exp(-a*abs(t)); % определение сигнала

s1=[zeros(1,2*length(t))  s  zeros(1,2*length(t))];

df=1/(dt*length(s1)); Fmax=1/dt; % задание частотной шкалы

f=-Fmax:df:Fmax;

omega = 2*pi*f;

S=2*a*K./(a^2 + omega.^2); % выражение комплексного спектра

subplot(3,1,1), plot(f,abs(S))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)