Информатика и выч. техника \ Теория и обработка сигналов

Спектральные представления непериодических сигналов. Вариант 7, страница 2

title('Амплитудный спектр, вычисленный по выражению (4)')

f=-(Fmax-df):2*df:Fmax;

y1=dftsum(s1); y1p=fftshift(y1);    % вычисление и сдвиг ДПФ

subplot(3,1,2), plot(f,abs(y1p)*dt, 'o')

set(gca,'FontName','Arial Cyr', 'FontSize',10)

title('Амлитудный спектр, вычисленный с помощью dftsum()'),grid

N=256; % число точек

Ts=T/(N-1); % интервал отсчетов

t=0:Ts:T; % временной интервал

x=K*exp(-a*abs(t));

Fmax=1/Ts; % максимальная частота

df=1/T; % частотное разрешение

f=-Fmax/2:df:Fmax/2; % частотная шкала

X=fft(x,N); % БПФ сигнала

Xp=fftshift(X); % частотный сдвиг

subplot(313), plot(f,abs(Xp)*Ts, 'o')

set(gca,'FontName','Arial Cyr', 'FontSize',10)

title('Амлитудный спектр, вычисленный с помощью fft()'),grid

В данном script-файле учтена связь преобразования Фурье непрерывного времени и дискретного преобразования Фурье, а именно:

НВПФ сигнала  на частотах 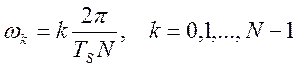 равно ДПФ,  умноженному  на значение интервала отсчетов ТS.

Полученный результат представлен на рис. 6.

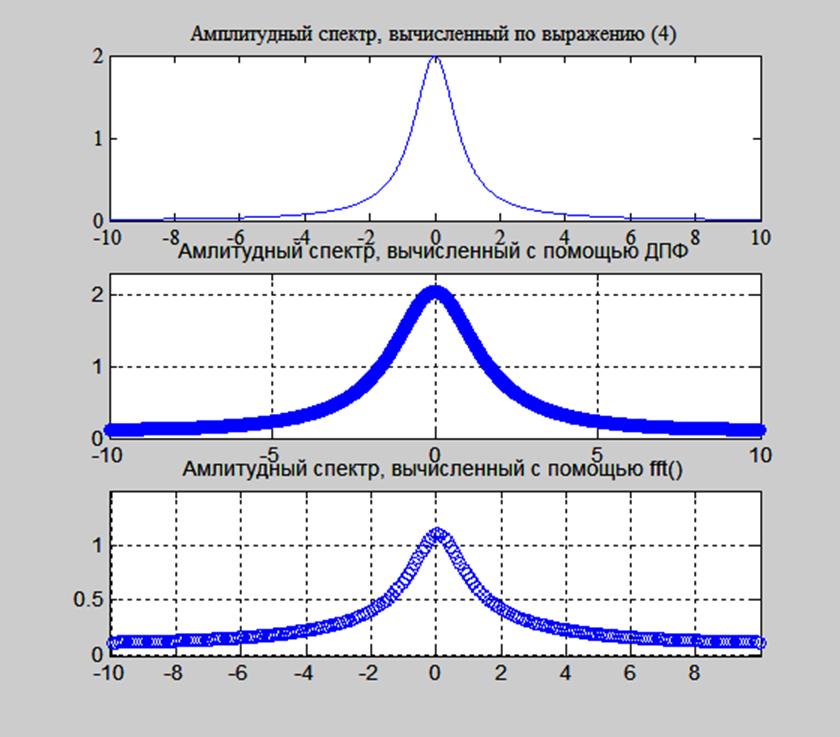
Рис. 6. Спектры сигнала, полученные с помощью НВПФ, ДПФ и функции fft(t).

последний график не совпадает.

Видим, что все графики спектров имеют одинаковую форму.

График спектра, полученного с помощью функции fft() имеет расхождения с другими вследствие недостаточной частоты отсчётов и быстрого изменения сигнала.

Аппроксимация тем точнее, чем меньше интервал отсчетов TS, в пределах которого сигнал не должен существенно измениться.

5. Изучение свойств преобразования Фурье.

5.1. Свойство линейности.

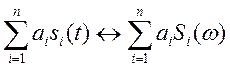Если , , то                                                                   (5)

Докажем данное свойство.

Выражение  значит, что  и  связаны через преобразование Фурье вида:

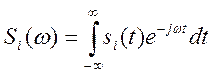                                                                                                  (6)

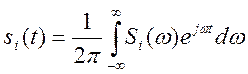                                                                                                                           (7)

Т.к. сумма интегралов равна интегралу суммы, получим:

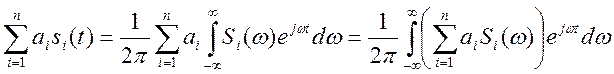                                                             (8)

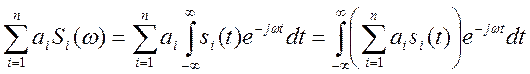                                                                           (9)

Значит, .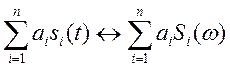

Следующий script-файл иллюстрирует свойство линейности преобразования Фурье.

N = 128; %  Длина сигналов

k = 0:N-1;

gamma = -0.5;

g = exp(gamma*k);

% g - экспоненциальная функция

h = sin(2*pi*k/(N/2));

figure(1),plot(k,g,k,h)

% h - синусоидальная последовательность с периодом = N/2

% вычисление преобразований Фурье сигналов

[G,w] = freqz(g,1,512);

[H,w] = freqz(h,1,512);

% Свойство линейности

alpha = 0.5;

beta = 0.25;

y = alpha*g+beta*h;

[Y,w] = freqz(y,1,512);

% Графики Y и  alpha*G+beta*H для проверки их равенства

figure(2), subplot(211),plot(abs(Y))

subplot(212), plot(abs(alpha*G+beta*H))

Результат выполнения данного script-файла представлен на рис. 7.

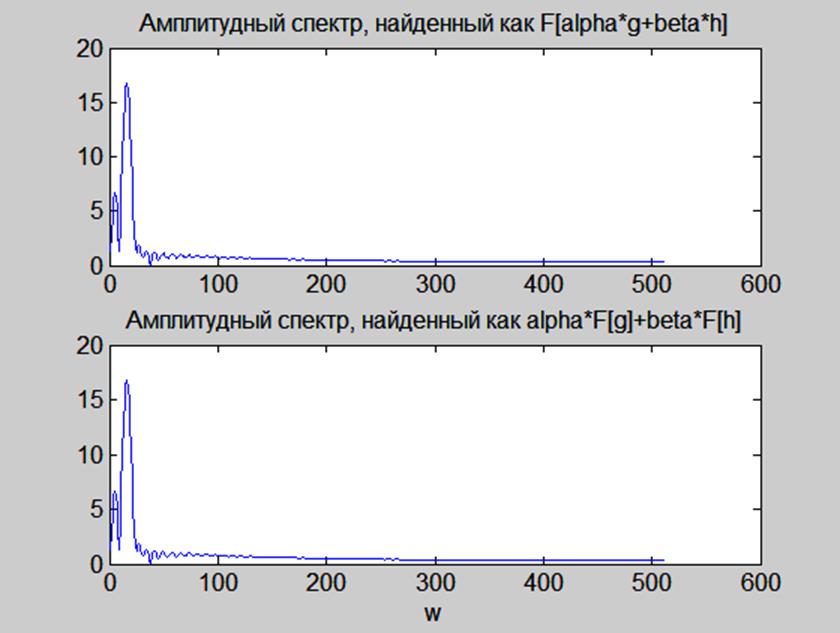
Рис. 7. Иллюстрация свойства линейности преобразования Фурье.

Видим, что графики совпадают, значит, свойство линейности выполняется.

5.2. Свойство временного сдвига.

Если , то                                                                              (10)

Докажем данное свойство.

Запишем 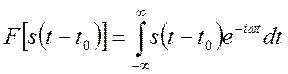 и обозначим .

Тогда

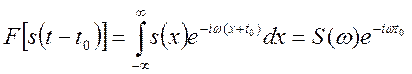.                                                                                 (11)

Значит, .                                                                                                    

Данное свойство показывает, что при сдвиге функции на  модуль  не изменяется, а сдвигается во времени на  каждая частотная составляющая s(t).

Следующий script-файл иллюстрирует свойство временного сдвига преобразования Фурье.

% Свойство временного сдвига

n0 = 12; % y2 - последовательность y, сдвинутая на 12 отсчетов

y2 = [zeros([1,n0]) g];

[Y2,w] = freqz(y2,1,512);

G0 = exp(-j*w*n0).*G;

% Графики амплитудных спектров

figure(3), subplot(211), plot(abs(G0))

subplot(212), plot(abs(Y2));

Результат выполнения данного script-файла представлен на рис. 8.

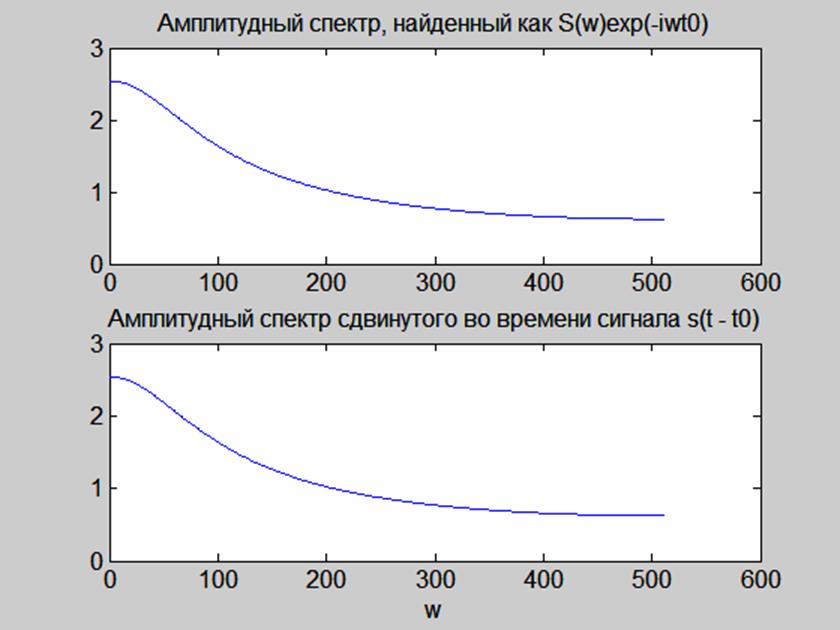
Рис. 8. Иллюстрация свойства временного сдвига преобразования Фурье.

Видим, что графики совпадают, значит, свойство временного сдвига выполняется.

5.3. Свойство изменения масштаба.

Если , то для любого действительного a 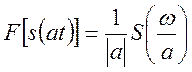  .                      (12)

Докажем данное свойство.

Пусть  и , тогда

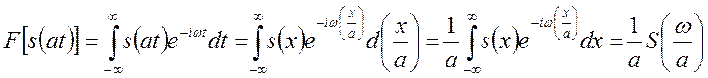                                           (13)          Аналогично для  получаем:

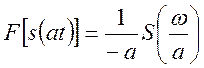                                                                                                                      (14)

Следовательно,  .                                                                                         

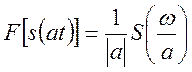Следующий script-файл иллюстрирует свойство изменения масштаба преобразования Фурье.

% Свойство изменения масштаба

a=0.1;% Коэффициент изменения масштаба

g1= exp(gamma*k*a);

figure(4),plot(k,g,k,g1) % Графики во временной области

[G,w] = freqz(g,1,512);

G1 = freqz(g1,1,512);

% Графики спектров

figure(5), subplot(211), plot(w,abs(G))

subplot(212), plot(w,abs(G1))

Результаты выполнения данного script-файла представлены на рис. 9 и рис. 10.

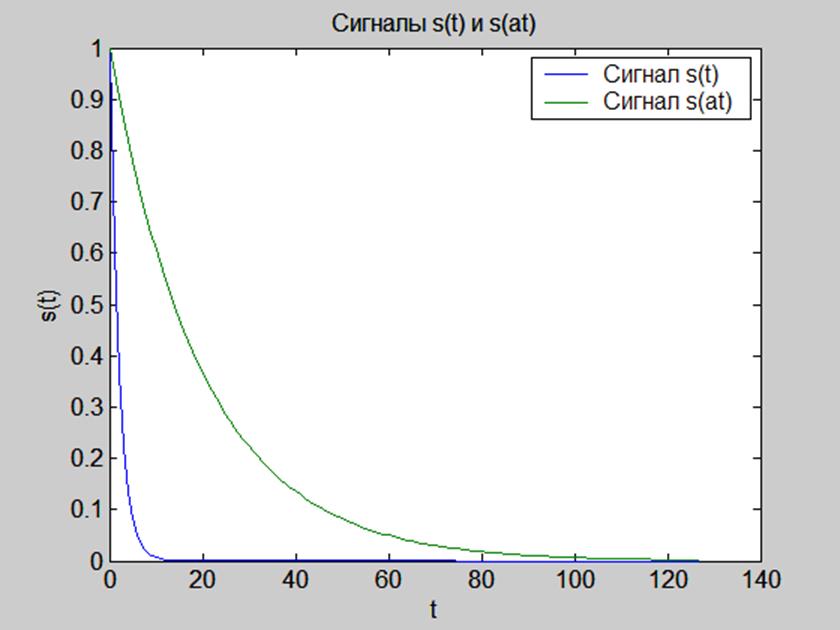
Рис. 9. Графики сигналов s(t) и s(at) во временной области.

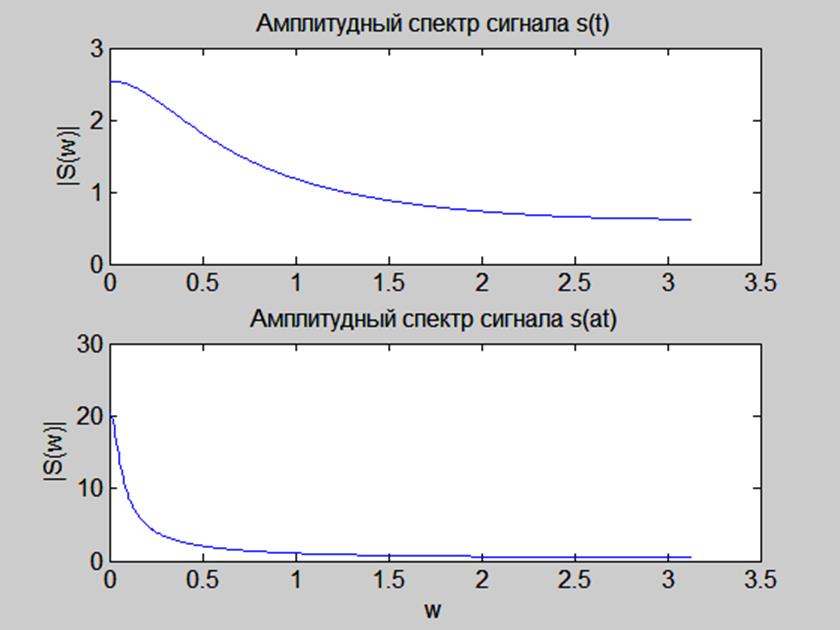
Рис. 10. Графики амплитудных спектров сигналов s(t) и s(at)  в частотной области.

Видим, что для a<1  s(at) представляет собой функцию s(t), растянутую во времени.

При этом амплитудный спектр сужается по оси частот.

Таким образом, чем шире сигнал по оси времени, тем уже его амплитудный спектр и наоборот.

5.4. Свойство свертки.

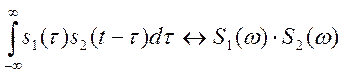Если , , то   .                         (15)

Докажем данное свойство.

Запишем преобразование Фурье свёртки

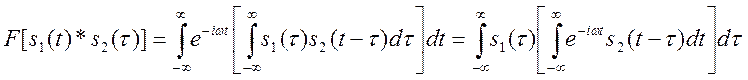                             (16)

Пусть , тогда

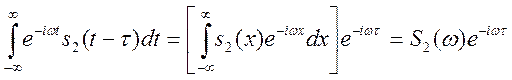                                                                 (17)

Следовательно,

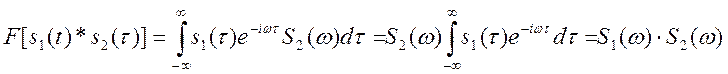                                   (18)

Таким образом, получили, что  .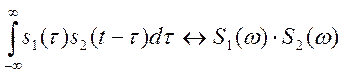

Следующий script-файл иллюстрирует свойство свертки преобразования Фурье.

% Свойство свертки

y5 = conv(g,h);

[Y5,w] = freqz(y5,1,512);

figure(6), subplot(211), plot(abs(Y5))

subplot(212), plot(abs(G.*H))

Результаты выполнения данного script-файла представлены на рис. 11.

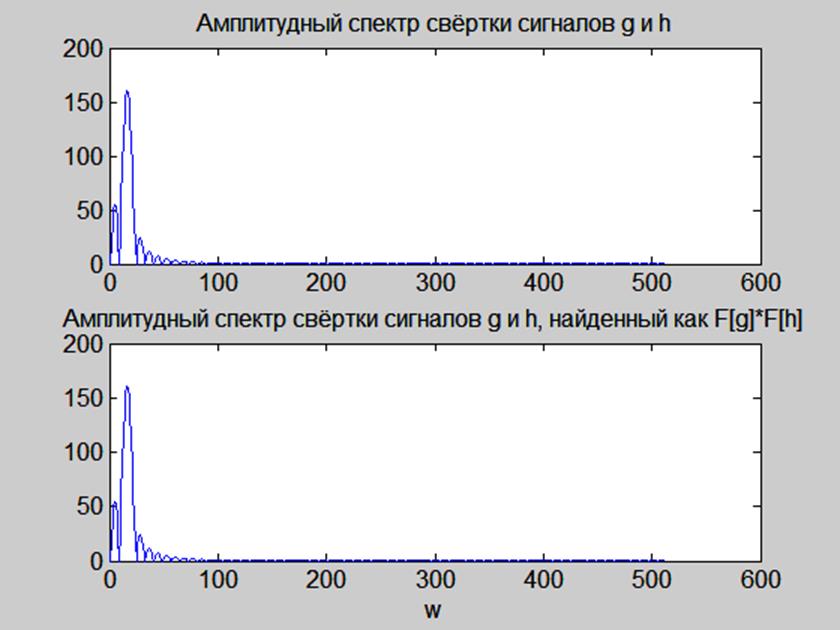
Рис. 11. Иллюстрация свойства свертки преобразования Фурье.

Видим, что графики совпадают, значит, свойство свёртки выполняется.

Выводы:

1.  Спектральное представление непериодических сигналов основывается на использовании преобразования Фурье, которое получается из ряда Фурье путём предельного перехода при .

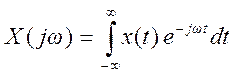                              - прямое преобразование Фурье, 

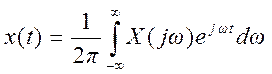                - обратное преобразование Фурье.

Функция X(jω) – спектральная плотность (плотность комплексных амплитуд гармоник, приходящихся на единичный интервал частот вблизи рассматриваемой частоты  ω).

2.  Амплитудный и фазовый спектры непериодического сигнала являются сплошными, в отличие от линейчатых спектров периодического сигнла.

Спектры сигнала полностью описывают его в частотной области.

3.  Для спектрального представления дискретных сигналов импользуется дискретное преобразование Фурье (ДПФ):

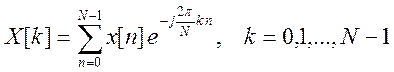
4.  Для вычисления ДПФ в Matlab существует функция fft().

ДПФ и НВПФ связаны, как  X = fft()*Ts, где Ts – интервал отсчётов.

Скачать файл