





НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов», 6-й семестр
ЛАБОРАТОРНАЯ РАБОТА № 12
СЛУЧАЙНЫЕ СИГНАЛЫ И ИХ ХАРАКТЕРИСТИКИ
Цель работы:изучение основных характеристик стационарных случайных сигналов (среднего значения, автокорреляционной функции, спектральной плотности мощности) и приобретение практических навыков их вычисления и анализа в среде Matlab.
Задание и порядок выполнения работы
1. Ознакомьтесь с теоретическими сведениями по статистическим характеристикам случайных сигналов, изложенными в учебной литературе, например, в [1, стр. 20-54] или [2, стр. 60-80, 91-93], а также в Приложении 1.
2.
Используя функцию randn(), сгенерируйте 500 отсчетов
случайного сигнала X с
нулевым математическим ожиданием и единичной дисперсией. Постройте график X.
Напишите Matlab- функции для вычисления оценок среднего и дисперсии
случайного сигнала, вычислите эти оценки для случайного сигнала X,
сравните полученные оценки с теоретическими значениями и объясните причины
различий.
Примечание. В Matlab имеются
встроенные функции mean() и var() для вычисления среднего и
выборочной дисперсии, используйте их для сопоставления результатов вычислений.
3. Постройте на одной фигуре, применяя subplot, график плотности вероятности нормальной случайной величины из п.2 и график гистограммы сигнала X с помощью функции hist() с числом интервалов N=15 – 20. Постройте также график гистограммы в масштабе плотности вероятности, используя, например, функции [N1,X1]=hist(X,N) и bar(). Объясните соответствие и различие результатов.
4.
Запишите выражение
автокорреляционной функции (АКФ) случайного дискретного сигнала и объясните смысл
корреляционной зависимости для сигнала.
Используя выражение связи между АКФ выходного ![]() и
входного сигналов
и
входного сигналов ![]() линейной дискретной системы
линейной дискретной системы
![]() , где h[m]- импульсная характеристика, определите аналитически АКФ
выходного сигнала для системы с уравнением из индивидуального задания
(Приложение 2) при входном сигнале в виде белого шума с АКФ
, где h[m]- импульсная характеристика, определите аналитически АКФ
выходного сигнала для системы с уравнением из индивидуального задания
(Приложение 2) при входном сигнале в виде белого шума с АКФ ![]() , при этом
, при этом ![]() -
дисперсия (мощность) шума,
-
дисперсия (мощность) шума, ![]() - единичный
дельта-импульс.
- единичный
дельта-импульс.
Найдите ту же функцию, используя процедуру conv() Matlab, в качестве входа рассматривайте случайный процесс X из п.2.
Постройте график ![]() . Объясните соответствие
полученных результатов.
. Объясните соответствие
полученных результатов.
5.
Сгенерируйте случайный сигнал X длительностью 1000 отсчетов, распределенный по
нормальному закону с нулевым средним значением и единичной дисперсией.
Используя уравнение системы (п.4, индивидуальное задание), вычислите выходной
сигнал Y.
Постройте на одной фигуре 4 графика рассеяния с помощью функции plot(X, Y, ‘.’) для четырех случаев:
а) (Yi, Yi+1), б) (Yi, Yi+2), в) (Yi, Yi+3), г) (Yi, Yi+4) (i
=1,2,…,900).
Фрагмент
программного кода с фильтром ![]()
» n=3:1000;
» Y(n)=X(n)-0.8*X(n-1)+X(n-2);
» i=1:900;
» Y0(i)=Y(i);
» Y1(i)=Y(i+1);
» subplot(2,2,1), plot(Y0,Y1,'.'), title('График рассеяния Yi,Yi+1')
Для выполнения фильтрации можно также использовать процедуру filter() Matlab.
Сделайте вывод о степени коррелированности значений случайного сигнала Y на основании характера диаграмм рассеяния.
6. Используя функцию xcorr() с параметром ‘biased’ (смещенная оценка), определите оценку автокорреляционной функции выходного сигнала при входном сигнале из п.2. Постройте на одной фигуре графики АКФ, полученных в п.4 и в п.6, и сопоставьте их.
7. С помощью той же функции xcorr() определите и постройте график взаимной корреляционной функции выходного и входного сигналов фильтра. Объясните поведение взаимной корреляционной функции.
8. Сгенерируйте гауссовский случайный сигнал с нулевым средним значением и дисперсией, равной 2, длительностью 1000 отсчетов. Определите частотную характеристику фильтра для индивидуального задания из Приложения 3. Гауссовский сигнал рассматривайте как входной сигнал фильтра. Используя в качестве прототипа программу из Приложения 4, постройте на одной фигуре графики АЧХ фильтра, спектральной плотности мощности входного и выходного сигналов. Объясните логический смысл результатов.
9. Составьте отчет по лабораторной работе. В отчете должны быть представлены
§ титульный лист,
§ название и цель работы,
§
формулировки пунктов работы,
команды и .m – файлы,
графики, комментарии, выводы.
Литература.
1. Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов. Учебное пособие. Новосибирск. Изд – во НГТУ, 1999 – ч.3.
2. Сергиенко А.Б. Цифровая обработка сигналов. - СПб.: Питер, 2003
Контрольные вопросы и упражнения
1. Перечислите основные статистические характеристики случайных сигналов и дайте их определения.
2. При каких условиях случайный сигнал является стационарным в широком смысле? Что это означает в поведении сигнала?
3.
Пусть для стационарного случайного
сигнала ![]() , определите средний квадрат сигнала.
, определите средний квадрат сигнала.
4. В среде Matlab сгенерируйте случайный сигнал, распределенный по равномерному закону, постройте его график, определите его среднее значение и выборочную дисперсию, сопоставьте с теоретическими значениями
5. Сформулируйте определение АКФ случайного сигнала, объясните физический смысл этой характеристики.
6. Запишите и объясните выражение (уравнение) связи АКФ выходного и входного сигналов ЛДС.
7.
В среде Matlab
сгенерируйте случайный сигнал, пропустите
его через фильтр ![]() и постройте
графики АКФ входного и выходного сигналов.
и постройте
графики АКФ входного и выходного сигналов.
8. Почему АКФ сигнала, сгенерированного с помощью процедуры randn() Matlab, имеет характер δ – импульса?
9. Дайте определение спектральной плотности мощности случайного сигнала и объясните её физический смысл.
10. Какой случайный процесс (сигнал) называют белым шумом?
11. Запишите и объясните выражение связи спектральных плотностей мощности выходного и входного сигналов ЛДС.
12.
В среде Matlab
сгенерируйте случайный сигнал и
пропустите его через фильтр ![]() . Постройте
графики спектральной плотности мощности входного и выходного сигналов и
объясните их поведение.
. Постройте
графики спектральной плотности мощности входного и выходного сигналов и
объясните их поведение.
Приложение 1. Краткие теоретические сведения.
Реальные сигналы, например, сигналы датчиков, аудиосигналы, видеосигналы являются случайными, т.е. обрабатываемый (наблюдаемый) сигнал представляет собой один из множества возможных сигналов. Случайные сигналы представляются как случайные процессы (функции). Пример случайного сигнала представлен на рис.1.
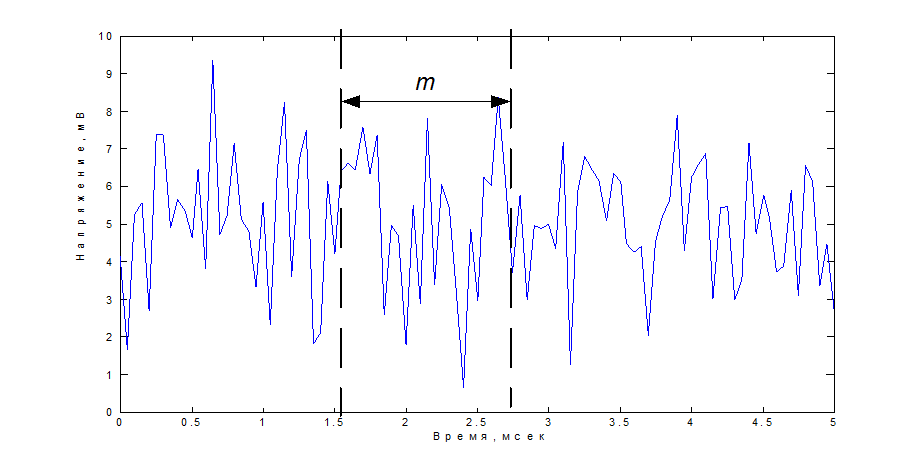
Рис.1.
В определенный момент времени случайный сигнал полностью определяется одномерным законом распределения – функцией распределения или плотностью распределения вероятностей. Наиболее важным законом распределения является нормальный, или гауссовский закон, у которого плотность вероятностей описывается выражением
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.