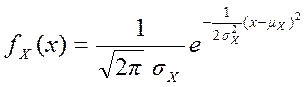, (1)
в
котором 
- математическое ожидание (среднее
значение), 
- дисперсия.
Оценки,
т.е приближенные значения среднего и дисперсии сигнала по независимым наблюдениям
определяются как
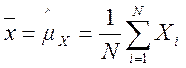, (2)
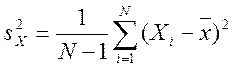. (3)
Эти
оценки являются состоятельными и несмещенными, т.е. при 
они
сходятся к и соответственно.
Случайные сигналы (процессы) подразделяются на непрерывные по времени (аргументу) и дискретные по времени. Дискретный по времени случайный сигнал Xn – это случайная последовательность, которая для каждого значения n представляет собой случайную величину.
Важной статистической характеристикой поведения случайного сигнала является его автокорреляционная функция (АКФ). Для стационарного в широком смысле (СШС) дискретного случайного процесса Xn автокорреляционная функция определяется выражением
(4)
при этом АКФ для СШС процессов не изменяется с изменением временного аргумента n, а зависит только от расстояния (сдвига) m. В выражении (4) M – это оператор математического ожидания, т.е. усреднения. Функция kXX[m] – четная функция своего аргумента m. АКФ определяет, как сильна связь между отсчетами сигнала, разделенными друг от друга интервалом m. Ясно, что для реальных случайных сигналов с увеличением интервала mмежду отсчетами степень связи должна ослабевать в связи с уменьшением влияния инерционности реального процесса. При m=0 значения АКФ дают средний квадрат.
Вид часто встречающейся на практике АКФ показан на рис.2
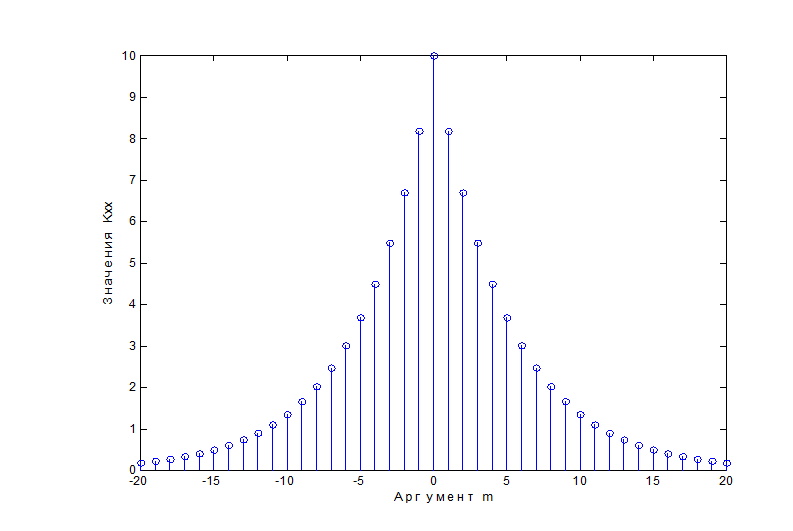
Рис.2.
В
частности, если X – последовательность независимой случайной переменной
с нулевым средним значением и дисперсией ,
то АКФ определяется выражением
. (5)
Такой
случайный процесс (сигнал) называют белым шумом, его значения Xn и Xn+m некоррелированы
для любого 
. Некоррелированность процесса
означает, что АКФ равна нулю и значения, разделенные соответствующим интервалом
m (лагом),
уже не зависят друг от друга.
Для реальных задач теоретическая АКФ может быть неизвестна. При этом оценка АКФ может быть определена по выражению
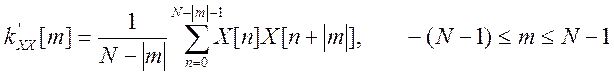, (6)
где N – число отсчетов (наблюдений) X.
Взаимная корреляционная функция (ВКФ), т.е. функция корреляции между двумя случайными процессами X и Y определяется выражением
(7)
В Matlab для вычисления оценок АКФ и ВКФ может использоваться функция xcorr().
Если белый шум, т.е. некоррелированный случайный процесс, проходит через фильтр (систему), то его выходной сигнал будет уже коррелированным процессом в силу инерционности динамической системы.
Связь между АКФ функциями дискретного по времени выходного и входного сигналов системы определяется выражением
. (8)
Здесь
h[m]-
импульсная характеристика системы, 
- символ
дискретной свертки.
В частотной области основной характеристикой стационарного случайного сигнала является его спектральная плотность мощности (спектр мощности), которая связана с автокорреляционной функцией преобразованием Фурье
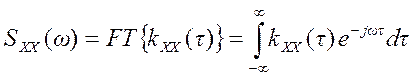. (9)
Для дискретного стационарного случайного сигнала
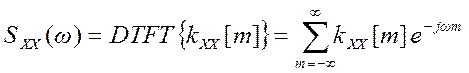. (10)
Спектральная плотность мощности определяется как
,
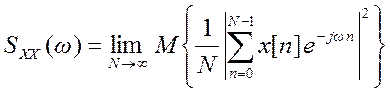(11)
т.е.
вычисляется ДВПФ последовательности 
, затем квадрат
его модуля и выполняется деление на длину последовательности. Далее вычисляется
математическое ожидание, т.е. проводится усреднение по всем возможным значениям
x, и производится предельный переход при .
Функция спектра мощности выражает распределение средней мощности процесса (сигнала) по частоте. Для белого шума спектр мощности равен постоянному значению на любой частоте. Эта константа называется интенсивностью белого шума.
Оценка спектра мощности по периодограмме (отрезку процесса длиной N отсчетов) эргодического сигнала производится по выражению
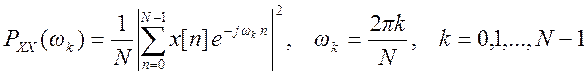, (12)
при этом для вычисления ДПФ используется быстрое преобразование Фурье (БПФ).
В Matlab для вычисления спектра мощности предусмотрена специальная процедура
[S,
f] = psd(x,
nfft, Fs), где x – вектор значений процесса,
nfft–
число элементов вектора, 
- частота
дискретизации сигнала.
Для линейной дискретной системы с частотной характеристикой H(ejω) связь между спектрами мощности выходного SYY(ω) и входного SXX(ω) сигналов определяется выражением
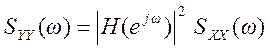. (13)
Приложение 2. Индивидуальные задания к п.4.
1.
2.
3.
4.
5.
6.
7. 
8.
9.
10.
11.
12.
Приложение 3. Индивидуальные задания к п.8.
1. 
2. 
3 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11.
12.
Приложение 4. Скрипт – файл к п. 8
% Формирование частотной шкалы
% и построение частотной характеристики фильтра
Ts=0.01; T=10; % интервал отсчетов и длительность сигнала
df=1/T; Fmax=1/Ts;
f=0:df:Fmax/2; % частотная шкала
d1=length(f);
% Частотная характеристика фильтра
H=0.5./(1-0.95*exp(-j*2*pi*f*Ts));
figure(1)
subplot(3,1,1), plot(f,abs(H))
title(' АЧХ фильтра')
% Вычисление и построение спектра мощности входного шума
t=0:Ts:T;
X=randn(1, length(t)); % Генерирование входного шума
[Sxx, f1]=psd(X,d1, Fmax); % Вычисление спектра мощности входа
subplot(3,1,2), stem(f1,Sxx), axis([0,15,0,6])
set(gca,'FontName', 'Times New Roman','FontSize', 12)
title(' Спектр мощности входа')
% Вычисление и построение спектра мощности выхода
i=2:length(X);
Y=zeros(1, length(X));
% Формирование выходного сигнала фильтра
b=0.5; a=[1, -0.95];
Y=filter(b,a,X);
[Syy, f2]=psd(Y,d1,Fmax); % Спектр мощности выхода
subplot(3,1,3), stem(f2,Syy), axis([0,15,0, 100])
title(' Спектр мощности выхода')
xlabel(' Частота, Гц')
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.