Решение систем нелинейных уравнений

6 страниц (Word-файл)

Министерство образования и науки Российской Федерации

Решение систем нелинейных уравнений.

Студент: Грунтова Л.Ю.

Группа: Ат-83

Вариант: 22

Проверил: Трошина Г.В.

Новосибирск, 2010г

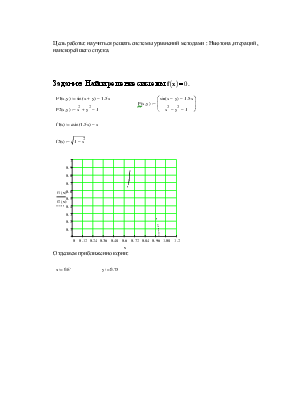
Цель работы: научиться решать системы уравнений методами : Ньютона ,итераций , наискорейшего спуска.

Задание: Найти решение системы .

Отделяем приближенно корни:

П о ф о р м у л е Н ь ю т о н а :

Ч и с л о и т е р а ц и й :

- т о ч н о с т ь

Метод Ньютона

Задаем формулу для определителя Вронского:

Зададим число итераций:

Результаты:

Метод итераций:

З а д а ё м о р и е н т и р о в о ч н о е ч и с л о и т е р а ц и й и н а ч а л ь н о п р и б л и ж е н и е (x0,y0)

В ы р а ж а е м (x,y) ч е р е з L(x,y), п о л у ч а е м и т е р а ц и о н н у ю ф о р м у л у .

Ч и с л о и т е р а ц и й :

Р е з у л ь т а т ы :

Метод наискорейшего спуска:

З а д а ё м о р и е н т и р о в о ч н о е ч и с л о и т е р а ц и й и н а ч а л ь н о п р и б л и ж е н и е (x0,y0)

Р е ш е н и е

Ч и с л о и т е р а ц и й :

Результаты:

Таблица результатов: