Изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ 
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

Дисциплина  «Теория  и  обработка  сигналов»

ЛАБОРАТОРНАЯ  РАБОТА  № 9

Линейные дискретные системы

Группа: АТ-23                                                                                  Преподаватель:                  

Студент:Кудрина Е.                                                                           Щетинин Ю.И.

Вариант: 1                   

Новосибирск

2004

Линейные дискретные системы

Цель работы:изучение методов анализа линейных дискретных стационарных (инвариантных во времени) систем и приобретение практических навыков  их анализа в среде Matlab.

1.

Проведем процедуру дискретизации аналогового фильтра, которая заключается в аппроксимации   линейного дифференциального уравнения фильтра разностным уравнением с помощью замены производных конечными разностями и последующих преобразований выражения к виду линейного разностного уравнения с постоянными коэффициентами.  При этом интервал между отсчетами сигналов (интервал дискретизации) выберем на основе теоремы отсчетов, частота отсчетов должна быть не менее чем в 2 раза выше верхней граничной частоты спектра обрабатываемого сигнала.
В результате дискретизации получим линейное разностное уравнение и передаточную функцию дискретной системы (фильтра).

Схема фильтра:

 

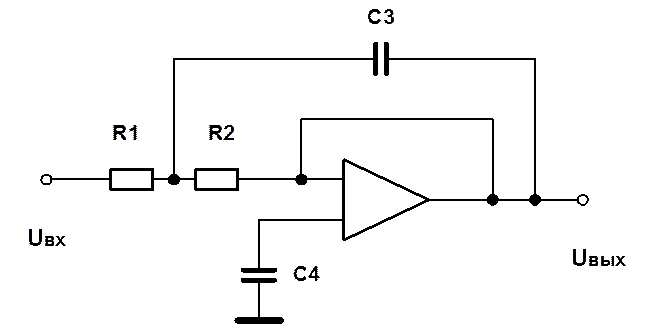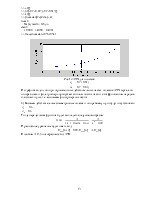
Рис.1 Схема активного фильтра нижних частот.

В предположении идеального операционного усилителя передаточная функция  фильтра имеет вид:

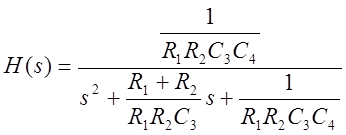
Если выбрать:  , то:

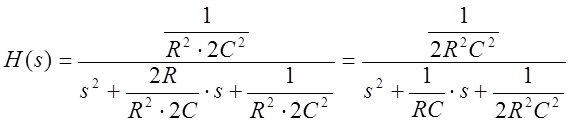          (1)

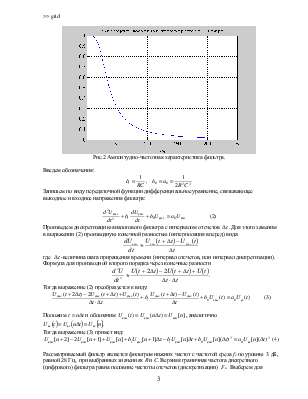
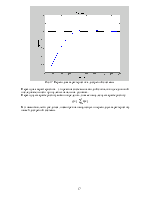
Для  С= 4 мкФ, R=1000 Ом амплитудно-частотная характеристика (АЧХ) фильтра имеет вид:

>> w=0:1500;

>> y=31250./(31250-power(w,2)+250*j*w);

>> plot(w./(2*pi),abs(y))

>> grid

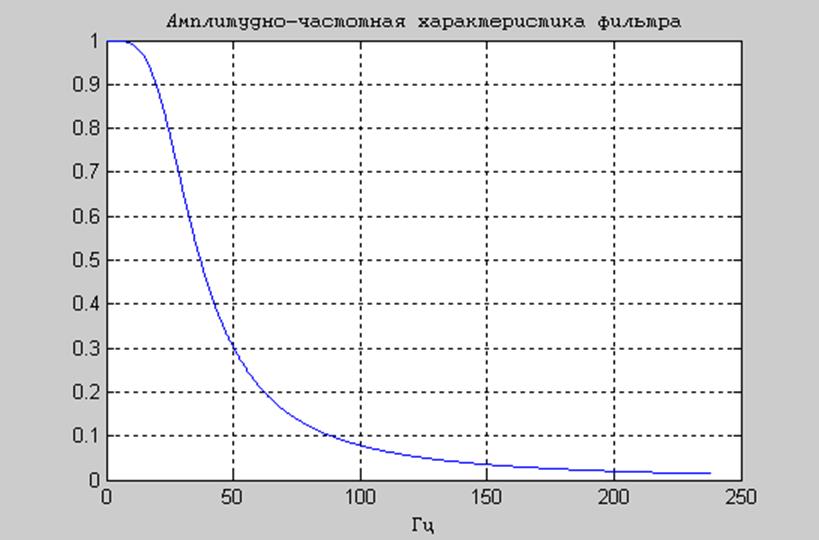
Рис.2 Амплитудно-частотная характеристика фильтра.

Введем обозначения:

,  

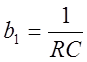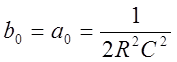
Запишем по виду передаточной функции дифференциальное уравнение, связывающее выходное и входное напряжения фильтра:

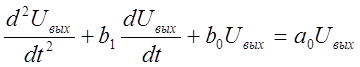                (2)

Произведем дискретизацию аналогового фильтра с интервалом отсчетов . Для этого заменим в выражении (2) производную конечной разностью (интерполяция вперед) вида:

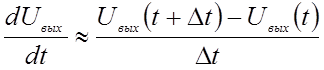
где  -величина шага приращения времени (интервал отсчетов, или интервал дискретизации).

Формула для производной второго порядка через конечные разности

.

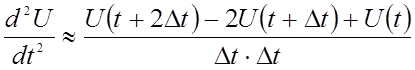Тогда выражение (2) преобразуется к виду:

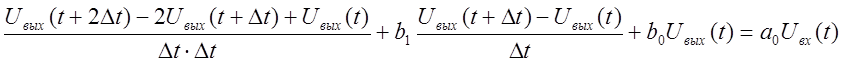         (3)

Положим и обозначим , аналогично .

Тогда выражение (3) примет вид:

 (4)

Рассматриваемый фильтр является фильтром нижних частот с частотой среза f_c по уровню  3 дБ, равной 28 Гц,  при выбранных значениях R и C. Верхняя граничная частота дискретного (цифрового) фильтра равна половине частоты отсчетов (дискретизации)  F_s.  Выберем для данного примера значение  F_s=10⁴ Гц, что соответствует интервалу (периоду) отсчетов     

Обозначим теперь коэффициенты разностного уравнения, как  ,  и . При этом разностное уравнение (4) можно представить в виде:

       (5)

Для выбранных числовых значений  значения коэффициентов равны:

, .

Тогда уравнение перепишем в виде:

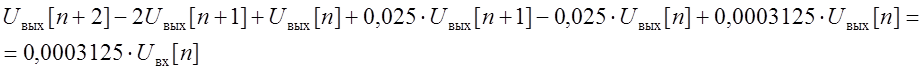     (6)

После преобразования:

                   (7)

Возьмем  Z- преобразование от левой и правой части уравнения (7). С учетом теоремы сдвига получим:

      (8)

Теперь  запишем передаточную функцию дискретного фильтра как отношение Z-преобразований выходного и входного сигналов:

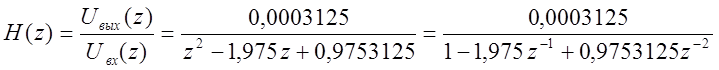     (9)

Частотная характеристика  дискретной системы представляет собой передаточную функцию при , т.е.  .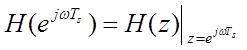

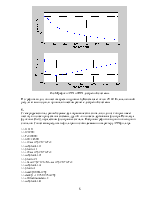
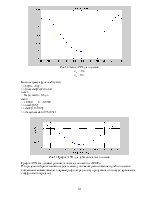
Ниже на рис.3 приведены АЧХ исходного аналогового и результирующего дискретного фильтра:

>> w=0:1500;

>> T=power(10,-4);

>> y1=0.0003125./(exp(2*j.*w.*T)-1.975.*exp(j.*w.*T)+0.9753125);

>> subplot(2,1,1)

>> plot(w./(2*pi),abs(y))

>> grid

>> subplot(2,1,2)

>> plot(w./(2*pi),abs(y1))

>> grid

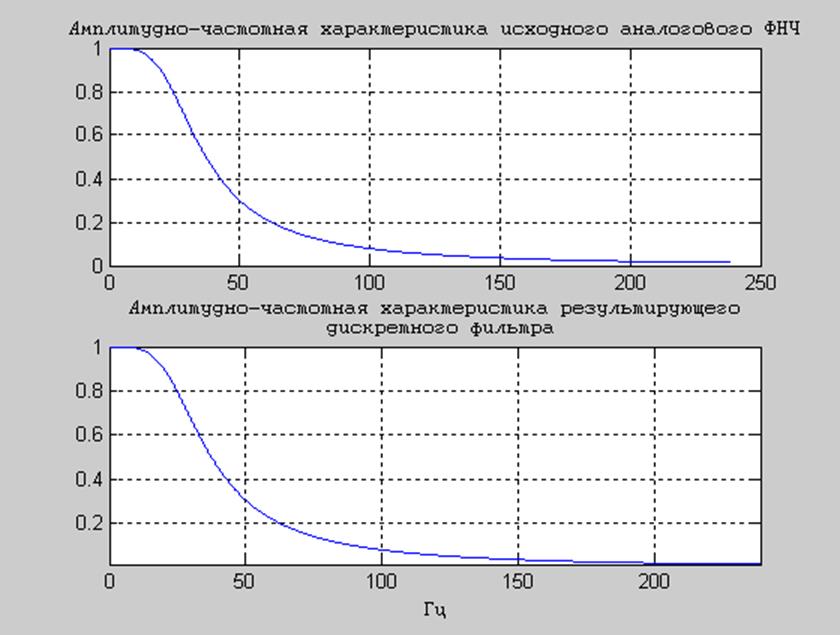
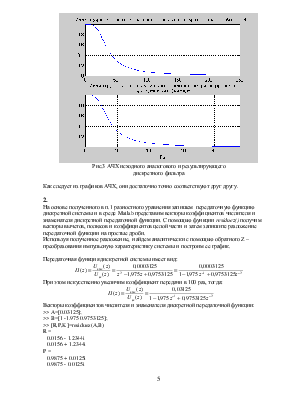
Рис.3 АЧХ исходного аналогового и результирующего

дискретного фильтра

Как следует из графиков АЧХ, они достаточно точно соответствуют друг другу.

2.

На основе полученного в п.1 разностного уравнения запишем  передаточную функцию дискретной системы и в среде Matlab представим векторы коэффициентов числителя и знаменателя дискретной передаточной функции. С помощью функции residuez() получим векторы вычетов, полюсов и коэффициентов целой части и затем запишите разложение передаточной функции на простые дроби.

Используя полученное разложение,  найдем аналитически с помощью обратного Z – преобразования импульсную характеристику системы и построим ее график.

Передаточная функция дискретной системы имеет вид:

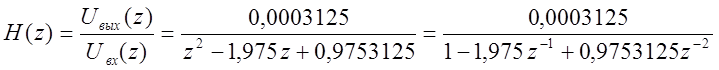
При этом искусственно увеличим коэффициент передачи в 100 раз, тогда:

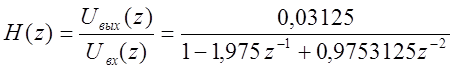
Векторы коэффициентов числителя и знаменателя дискретной передаточной функции:

>> A=[0.03125];

>> B=[1 -1.975 0.9753125];

>> [R,P,K]=residuez(A,B)

R =

   0.0156 - 1.2344i

   0.0156 + 1.2344i

P =

   0.9875 + 0.0125i

   0.9875 - 0.0125i

K =

     []

Общий вид разложения:

       B(z)           r(1)                       r(n)

       ---- = ----------------  +... ----------------  + k(1) + k(2)z^(-1) ...

       A(z)   1-p(1)z^(-1)          1-p(n)z^(-1)

Тогда разложение передаточной функции на простые дроби будет выглядеть следующим образом:

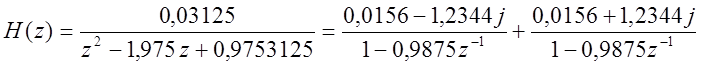
С помощью обратного Z-преобразования найдем импульсную характеристику системы:

Тогда:

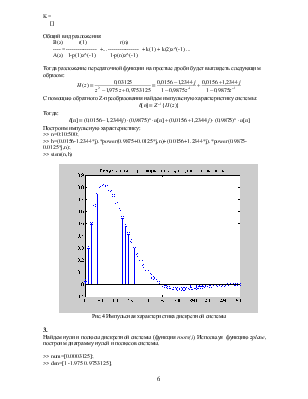
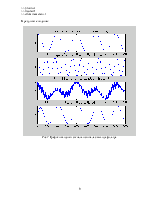
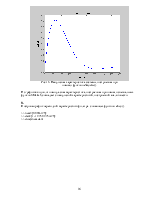
Построим импульсную характеристику:

>> n=0:10:500;

>> h=(0.0156-1.2344*j).*power(0.9875+0.0125*j,n)+(0.0156+1.2344*j).*power(0.9875-0.0125*j,n);

>> stem(n,h)

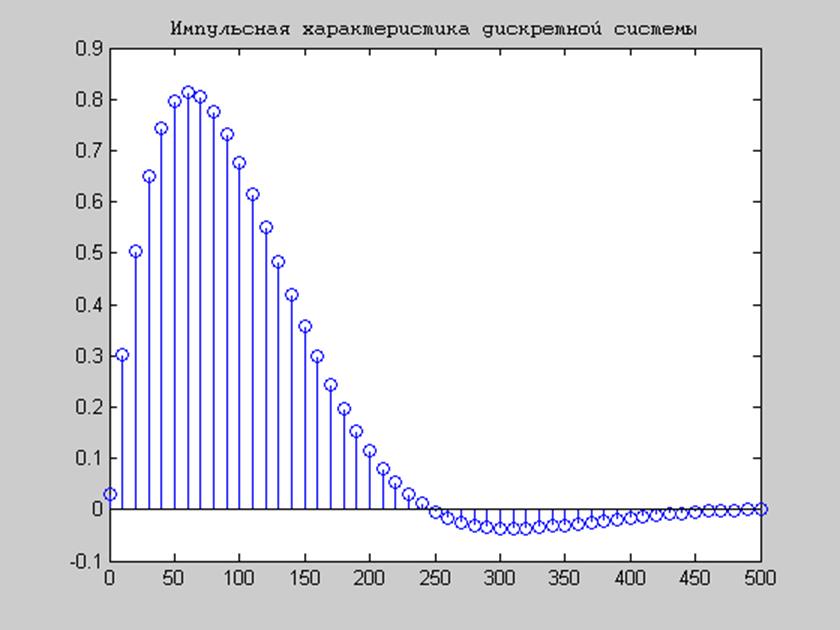
Рис.4 Импульсная характеристика дискретной системы

3.

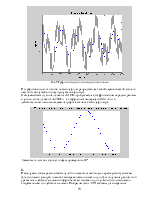
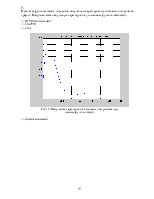
Найдем нули и полюсы дискретной системы (функция roots()). Используя  функцию zplane, построим диаграмму нулей и полюсов системы.

>> num=[0.0003125];

>> den=[1 -1.975 0.9753125];

Нули системы:

>> nul=roots(num)

nul =

   Empty matrix: 0-by-1

Полюса системы:

>> pol=roots(den)

pol =

   0.9875 + 0.0125i

   0.9875 - 0.0125i

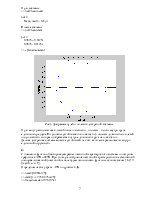
>> zplane(num,den)

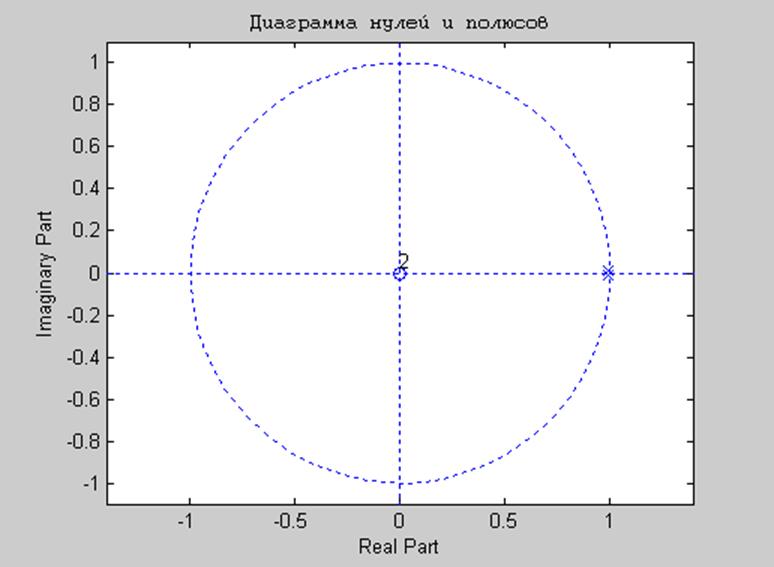
Рис.5 Диаграмма нулей и полюсов дискретной системы.

Нули могут располагаться в любой точке плоскости z, полюсы – только внутри круга единичного радиуса. По условию устойчивости в плоскости p полюсы должны быть в левой полуплоскости, которая отображается внутрь единичного круга на плоскости z.