Данная дискретная система является устойчивой, так как ее полюса расположены внутри единичной окружности.
4.
С помощью функции freqz
проведем расчет частотной характеристики системы и построим
графики её АЧХ и ФЧХ. При этом для построения частотной характеристики в
естественной (ненормализованной) частотной шкале будем использовать
функцию с синтаксисом [h,
f] = freqz(b, a,
n, Fs).
Определим частоту среза АЧХ по уровню 3 дБ.
>> num=[0.0003125];
>> den=[1 -1.975 0.9753125];
>> freqz(num,den,10^5,10^4)
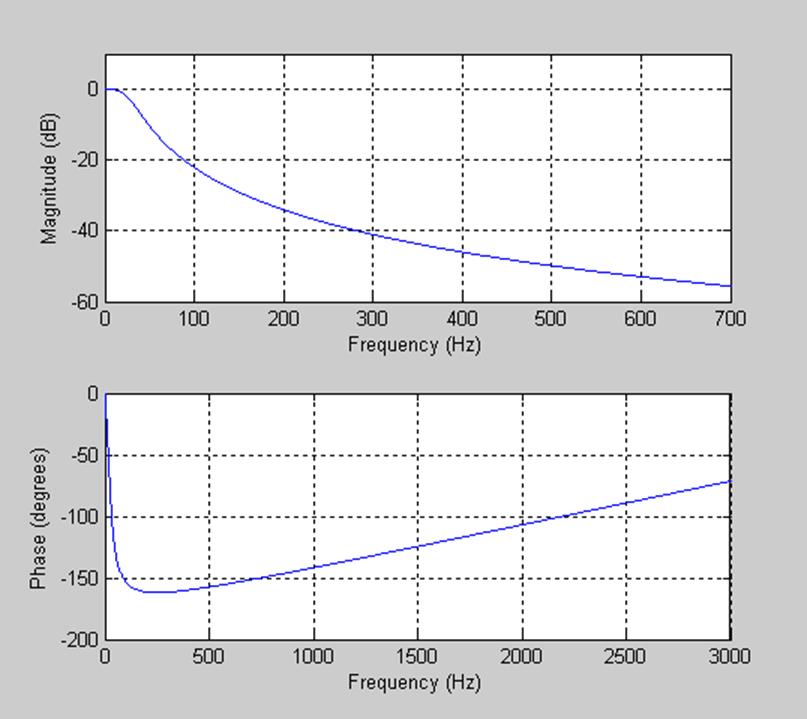
Рис.6 Графики АЧХ и ФЧХ дискретной системы.
Из графика видно, что частота среза по уровню 3дБ составляет около 28÷30 Гц, аналогичный результат мы получили при аналитическом расчете дискретной системы.
5.
Сгенерируем сигнал, равный сумме двух гармонических
сигналов, один из которых имеет частоту в полосе пропускания системы, другой -
в полосе задерживания фильтра. Используя функцию filter(), осуществим
фильтрацию сигнала. Построим графики входного и выходного сигналов.
Сопоставим результаты фильтрации с ожидаемыми по характеру АЧХ
фильтра.
>> f1=10;
>> f2=200;
>> Fs=10000;
>> n=0:1:4500;
>> x1=cos(2*pi*f1*n/Fs);
>> subplot(4,1,1)
>> plot(n,x1)
>> x2=cos(2*pi*f2*n/Fs);
>> subplot(4,1,2)
>> plot(n,x2)
>> x=cos(2*pi*f1*n/Fs)+cos(2*pi*f2*n/Fs);
>> subplot(4,1,3)
>> plot(n,x)
>> num=[0.0003125];
>> den=[1 -1.975 0.9753125];
>> z=filter(num,den,x);
>> subplot(4,1,4)
>> plot(n,z)
>> figure(2)
>> dlsim(num,den,x)
В результате получим:
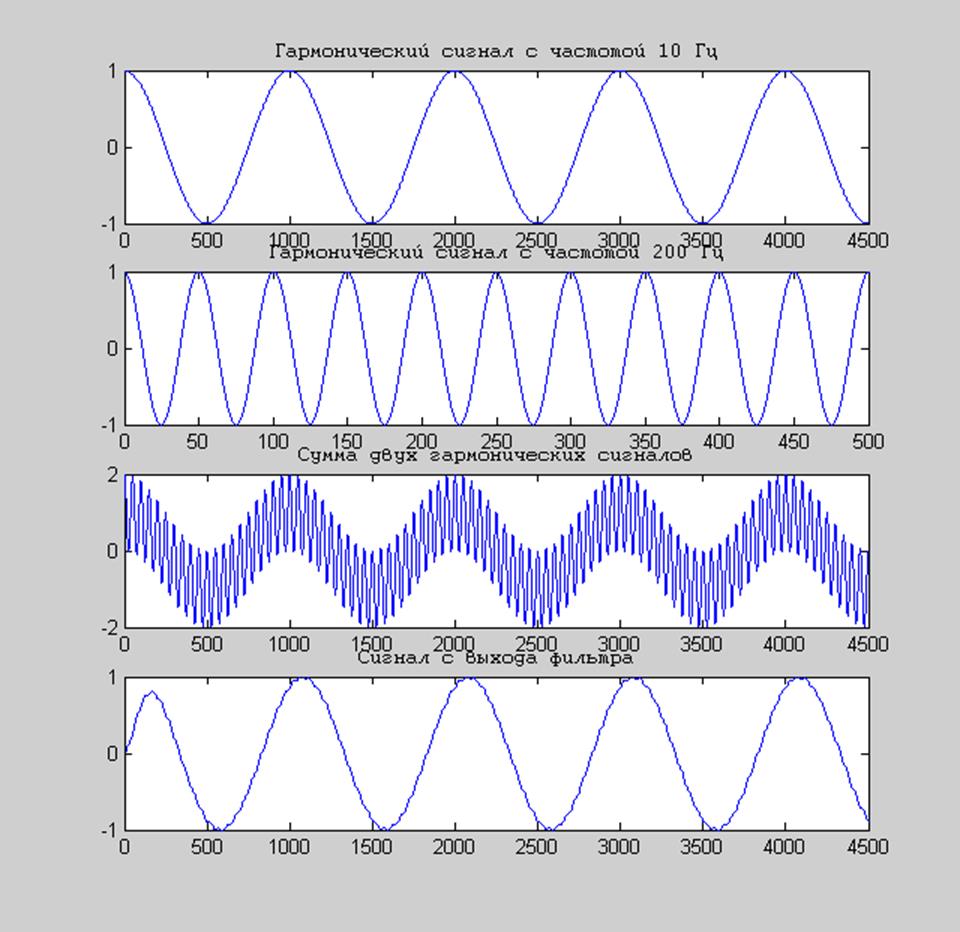
Рис.7 Графики входного сигнала и сигнала с выхода фильтра
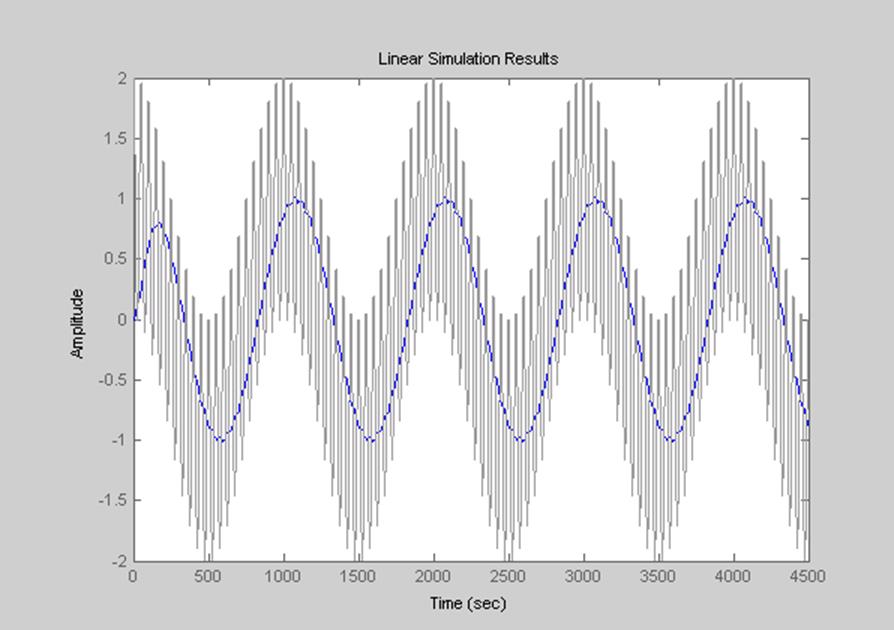
Рис.8 Графики входного и выходного сигналов
Из графиков видно, что сигнал с выхода фильтра представляет собой гармонический сигнал с частотой, входящей в полосу пропускания фильтра.
Ожидаемый выход: сигнал с частотой 10 Гц пропускается с коэффициентом передачи равным единице, сигнал с частотой 200 Гц – с коэффициентом передачи 0,02, что и в действительности мы наблюдаем на графике сигнала с выхода фильтра:
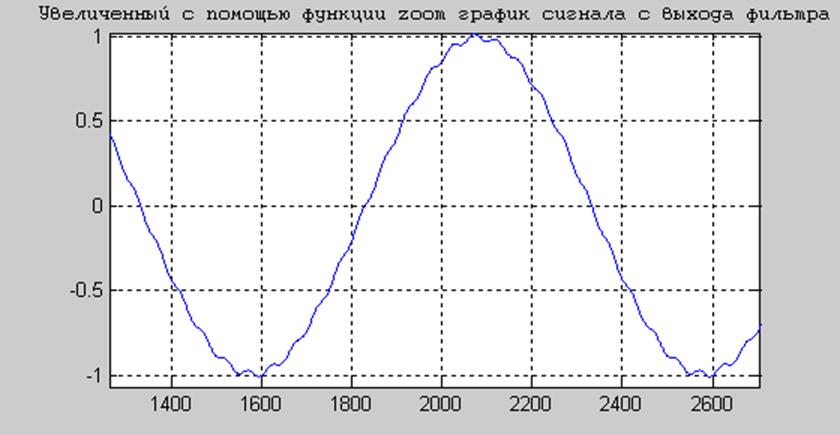
Заметим, что сигнал сдвинут по фазе примерно на 30°.
6.
Исследуем влияние расположения нулей и полюсов на частотную характеристику системы. Для этого методом проб и ошибок выберем новые полюса и нули. Для получения разностного уравнения с действительными коэффициентами полюса и нули должны быть комплексно сопряженными или действительными. Изобразим эскиз АЧХ системы для выбранных значений нулей и полюсов. Затем с помощью функции zp2tf() преобразуем полюсно - нулевое представление системы в передаточную функцию. Построим АЧХ системы по её передаточной функции и сравним с эскизом АЧХ.
1) Возьмем следующие полюса:
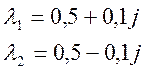
Нули пусть отсутствуют. Тогда передаточная функция будет выглядеть следующим образом:
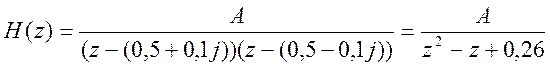
И разностное уравнение будет иметь вид:
![]()
Положим А=0,5 и изобразим эскиз АЧХ:
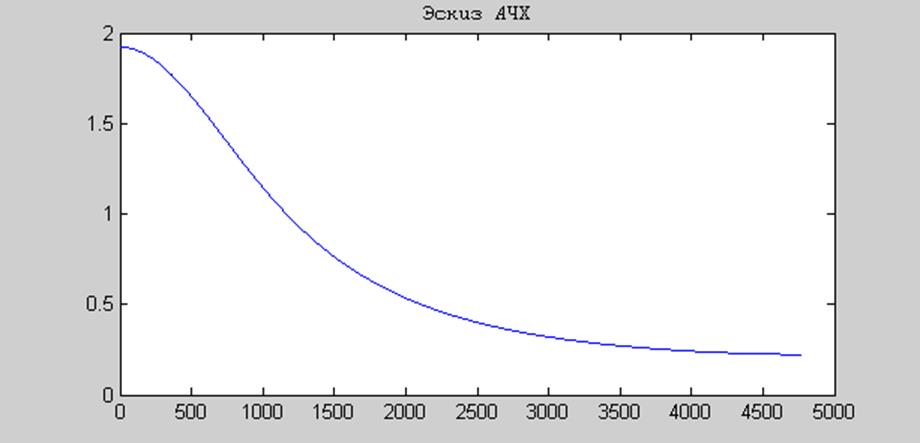
Рис.9 Эскиз АЧХ для полюсов
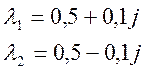
Воспользуемся функцией zp2tf():
>> z=[];
>> p=[0.5+0.1*j 0.5-0.1*j];
>> k=[];
>> [num,den]=zp2tf(z,p,k)
num =
Empty matrix: 0-by-3
den =
1.0000 -1.0000 0.2600
>> freqz(num,den,10^5,10^4)
В результате получим:
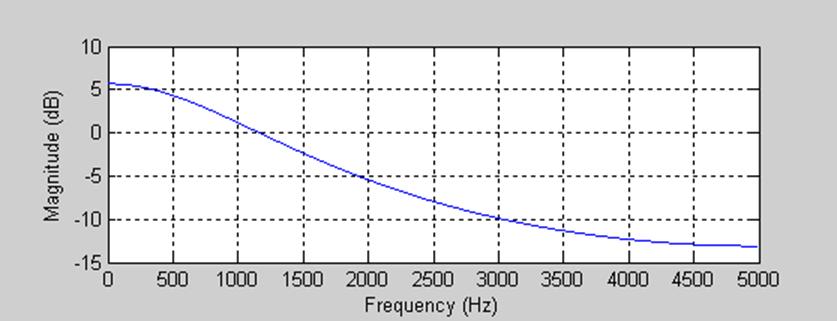
Рис.10 АЧХ для полюсов
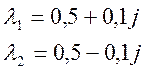
Как видно из графика при уменьшении действительных частей полюсов АЧХ поднялась выше и полоса пропускания значительно увеличилась – от 30 Гц до 700¸800 Гц.
2) Выберем полюса с отрицательной действительной частью, а нули по-прежнему будут отсутствовать:
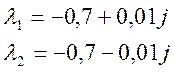
Тогда передаточная функция будет выглядеть следующим образом:
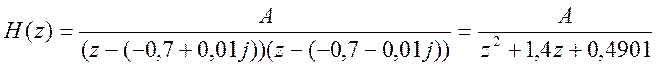
И разностное уравнение будет иметь вид:
![]()
Положим А=0,5 и изобразим эскиз АЧХ:
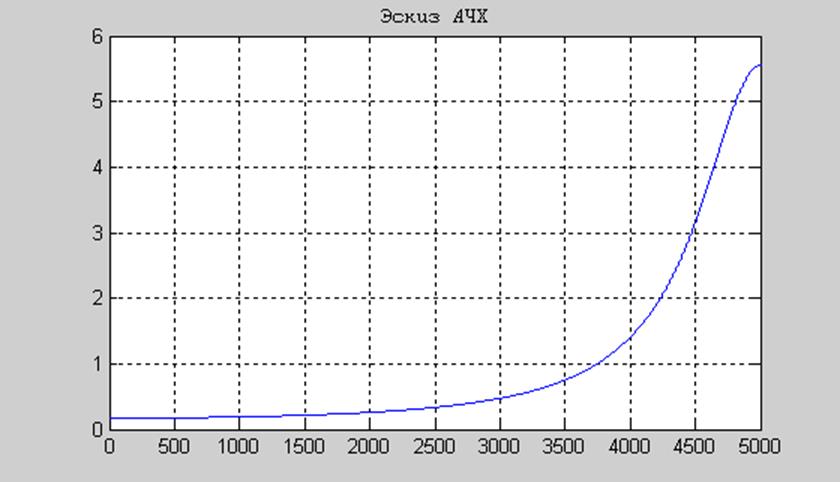
Рис.11 Эскиз АЧХ для полюсов
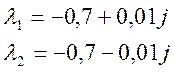
Воспользуемся функцией zp2tf():
>> z=[];
>> p=[-0.7+0.01*j -0.7-0.01*j];
>> k=[];
>> [num,den]=zp2tf(z,p,k)
num =
Empty matrix: 0-by-3
den =
1.0000 1.4000 0.4901
>> freqz(num,den,10^5,10^4)
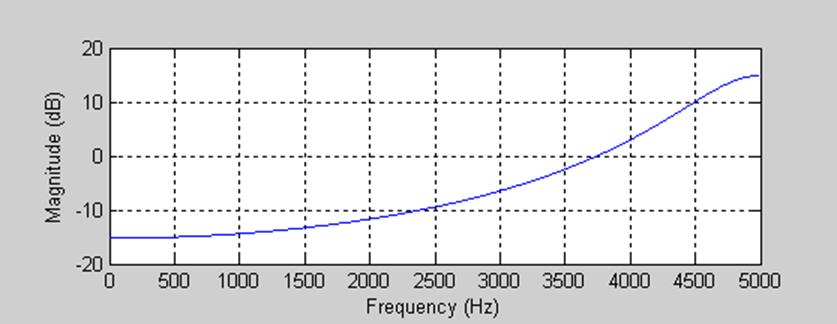
Рис.12 АЧХ для полюсов
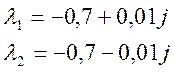
Из графика видно, что при отрицательных действительных частях полюсов АЧХ зеркально отобразилась и фильтр теперь пропускает сигналы низких частот с коэффициентом передачи близким к нулю, т.е. мы имеем фильтр верхних частот.
3) Возьмем действительные симметричные полюса и по прежнему нули будут отсутствовать:
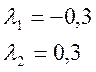
Тогда передаточная функция будет выглядеть следующим образом:
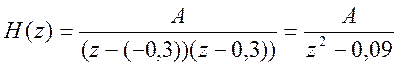
И разностное уравнение будет иметь вид:
![]()
Положим А=0,5 и изобразим эскиз АЧХ:
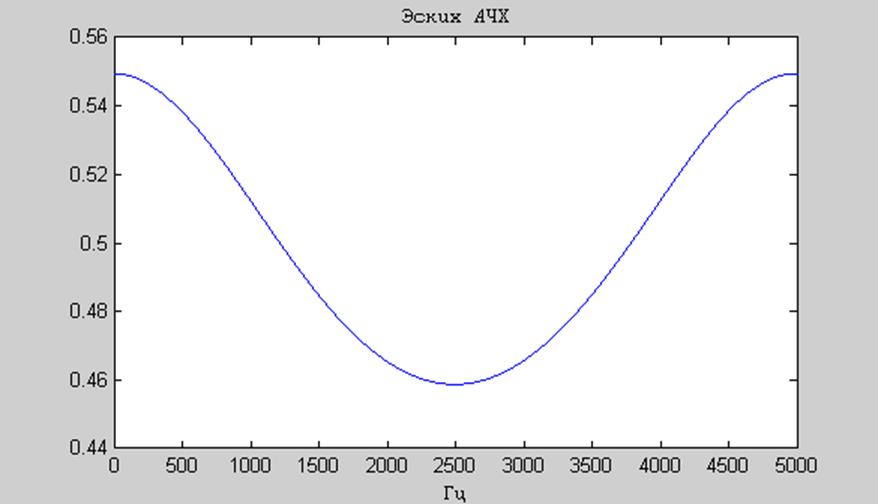
Рис.13 Эскиз АЧХ для полюсов
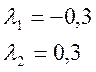
Воспользуемся функцией zp2tf():
>> p=[0.3 -0.3];
>> [num,den]=zp2tf(z,p,k)
num =
Empty matrix: 0-by-3
den =
1.0000 0 -0.0900
>> num=[0.5];
>> den=[1 0 -0.09];
>> freqz(num,den,10^5,10^4)
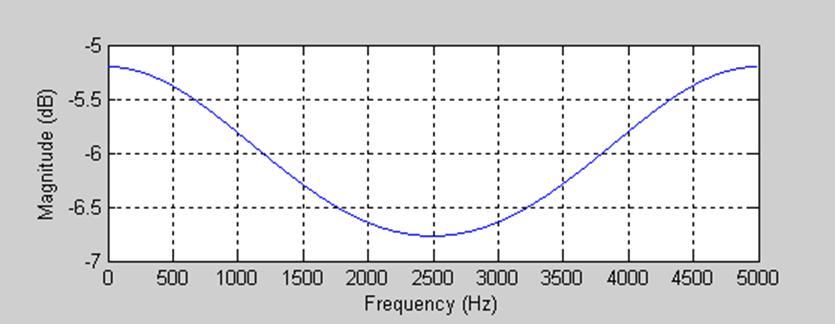
Рис.14 График АЧХ для действительных полюсов
График АЧХ стал симметричным относительно частоты 2500 Гц.
Из проделанной работы можно сделать вывод, что меняя расположение нулей и полюсов системы мы можем изменять параметры фильтра (полосу пропусканя и полосу задерживания, коэффициент передачи).
7.
Используя функцию impz(), определим импульсную характеристику системы и построим её график. Построим также импульсную характеристику с помощью функции dimpulse().
>> [H,T]=impz(num,den);
>> plot(T,H)
>> grid
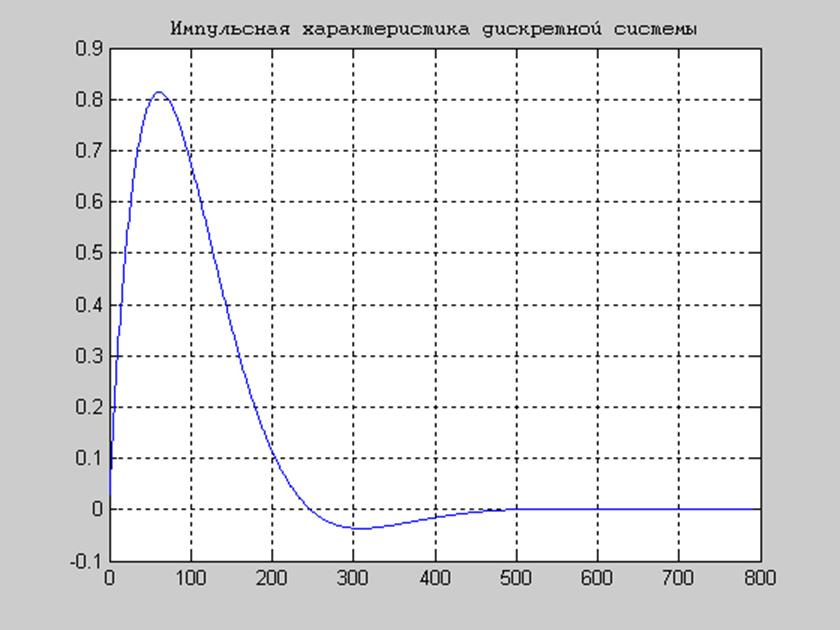
Рис.15 Импульсная характеристика системы, построенная при
помощи функции impz().
>> dimpulse(num,den)
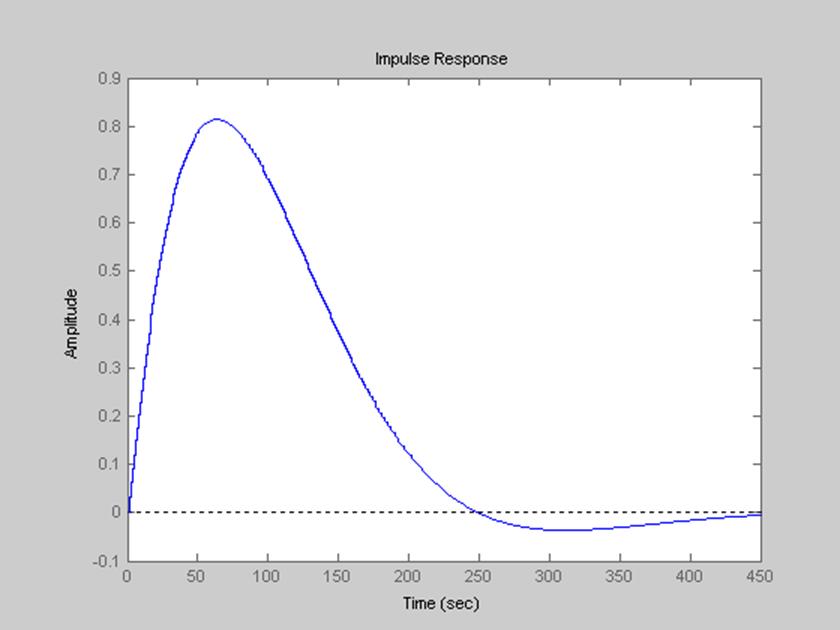
Рис.16 Импульсная характеристика системы, построенная при
помощи функции dimpulse().
Из графиков видно, что импульсная характеристика, построенная при помощи специальных функций Matlab, совпадает с импульсной характеристикой, построенной аналитически.
8.
Построим график переходной характеристики фильтра с помощью функции dstep().
>> num=[0.0003125];
>> den=[1 -1.975 0.9753125];
>> dstep(num,den)
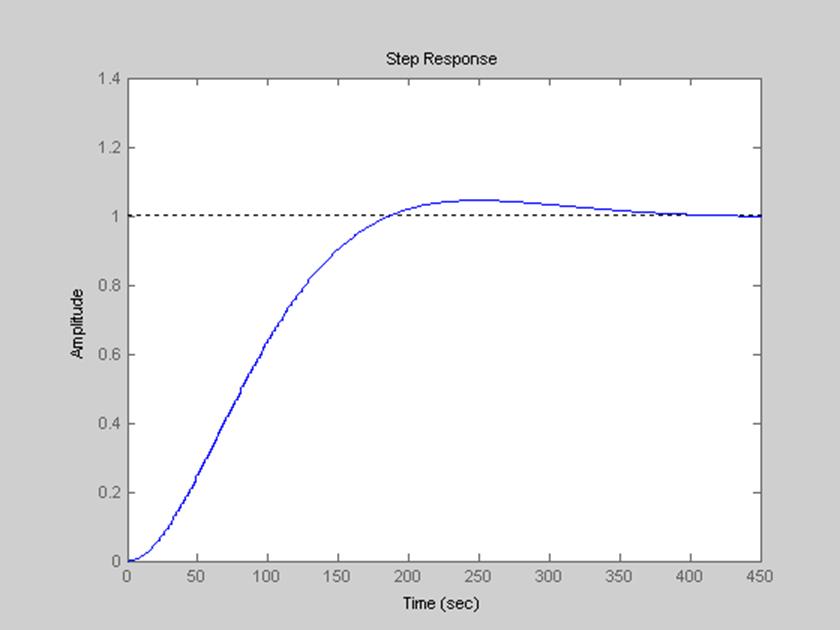
Рис.17 Переходная характеристика дискретной системы.
Переходная характеристика – это реакция системы на входной сигнал в виде единичной последовательности при нулевых начальных условиях.
Переходную характеристику можно определить, зная ее импульсную характеристику:
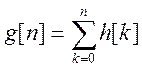
В этом можно легко убедиться, посмотрев на импульсную и переходную характеристику нашей дискретной системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.