





Новосибирский Государственный Технический Университет
Факультет Автоматики и Вычислительной Техники
Кафедра ССОД
Дисциплина «Теория и обработка сигналов»
Лабораторная работа № 7
ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ
СТАЦИОНАРНЫЕ СИСТЕМЫ
ВАРИАНТ №1
Выполнил: Преподаватель:
Пархоменко А.А. доц. Щетинин Ю.И.
Группа: АТ-53
Новосибирск, 2007
Цель работы:знакомство с динамическими характеристиками линейных непрерывных стационарных (инвариантных во времени) систем и их использованием для анализа систем в среде MATLAB.
1) Определение передаточной функции активного фильтра.
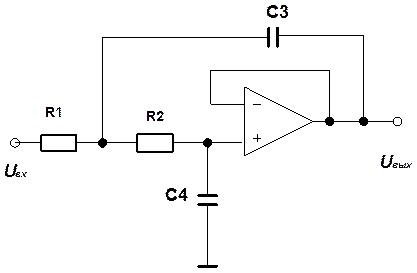
При этом операционный усилитель предполагается идеальным с бесконечно большим коэффициентом усиления и бесконечным входным сопротивлением.
Условия:
![]() ,
R=1000 Ом, С=0,5 мкФ.
,
R=1000 Ом, С=0,5 мкФ.
Решение:

Так как операционный усилитель
идеальный, то ![]() .
.
По 1 закону Кирхгофа для узла 1 получаем:
![]() (1)
(1)
Для данного фильтра: 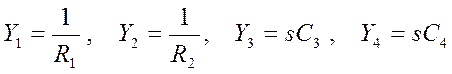 (2)
(2)
Тогда преобразуем (1):
![]() (3)
(3)
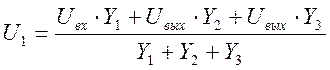 (4)
(4)
По 1 закону Кирхгофа для узла 2 получаем:
![]() (5)
(5)
![]() (6)
(6)
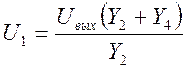 (7)
(7)
Подставим (4) в (7) и получим:
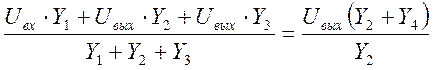 (8)
(8)
Передаточная функция фильтра -
это отношение преобразований Лапласа выходного и входного сигнала. Преобразуем
(8) к виду: 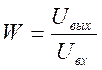
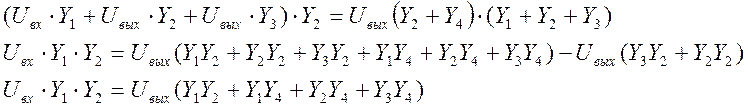
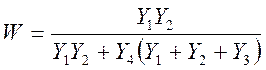 (9)
(9)
Подставляем (2) в (9) и получим:
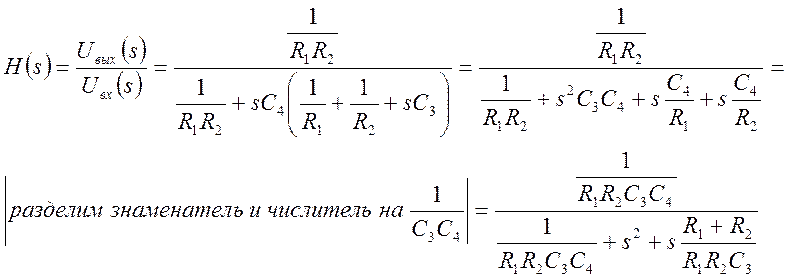
При ![]() ,
R=1000 Ом, С=0,5 мкФ получим:
,
R=1000 Ом, С=0,5 мкФ получим:
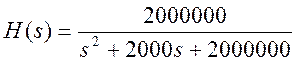
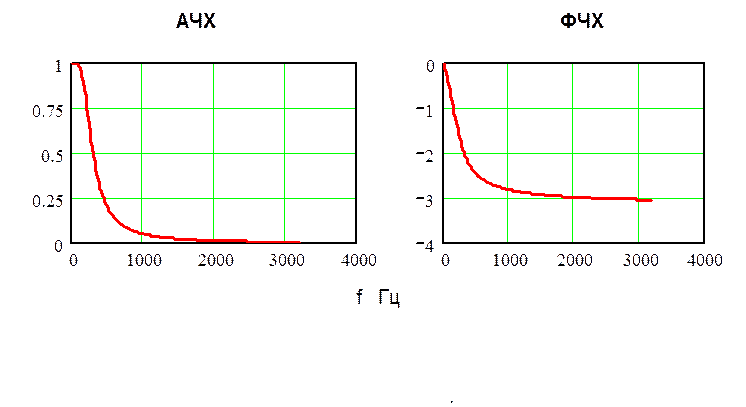
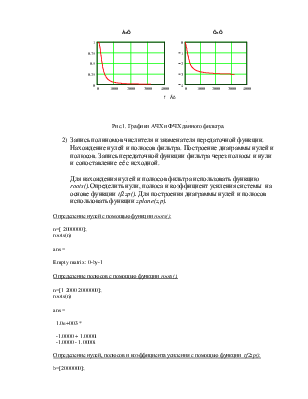
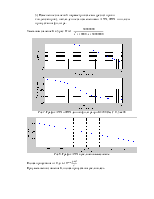
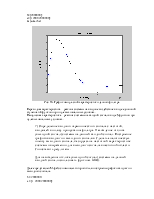
Рис.1. Графики АЧХ и ФЧХ данного фильтра.
2) Запись полиномов числителя и знаменателя передаточной функции. Нахождение нулей и полюсов фильтра. Построение диаграммы нулей и полюсов. Запись передаточной функции фильтра через полюсы и нули и сопоставление её с исходной.
Для нахождения нулей и полюсов фильтра использовать функцию roots().Определить нули, полюса и коэффициент усиления системы на основе функции tf2zp(). Для построения диаграммы нулей и полюсов использовать функции zplane(z,p).
Определение нулей с помощью функции roots():
n=[ 2000000];
roots(n)
ans =
Empty matrix: 0-by-1
Определение полюсов с помощью функции roots():
n=[1 2000 2000000];
roots(n)
ans =
1.0e+003 *
-1.0000 + 1.0000i
-1.0000 - 1.0000i
Определение нулей, полюсов и коэффициента усиления с помощью функции tf2zp():
b=[2000000];
a=[1 2000 2000000];
[z, p, k]=tf2zp(b, a)
z =
Empty matrix: 0-by-1
p =
1.0e+003 *
-1.0000 + 1.0000i
-1.0000 - 1.0000i
k =
2000000 % 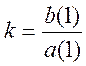
Диаграмма нулей и полюсов, построенная с помощью функции zplane(z,p):
b=[2000000];
a=[1 2000 2000000];
zplane(b,a)
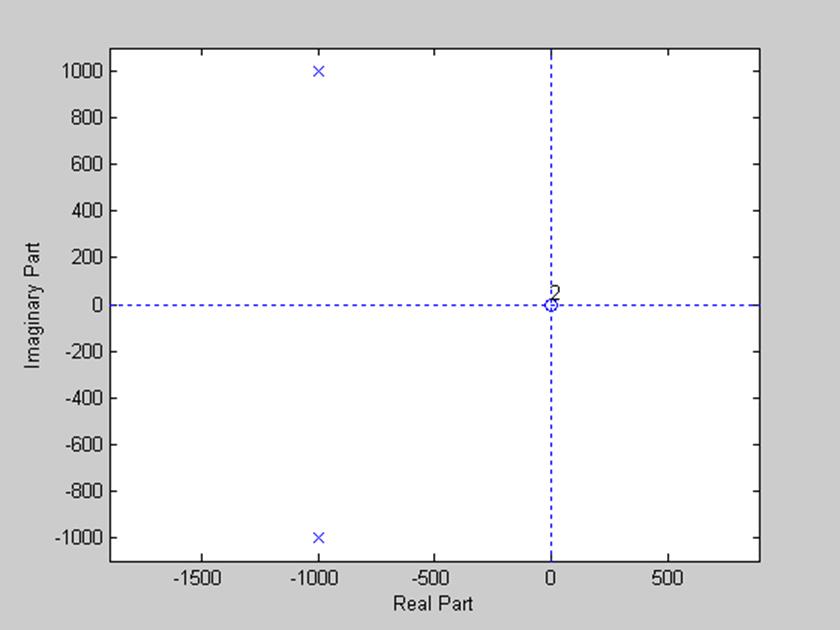
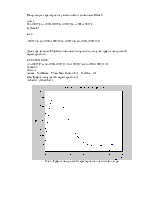
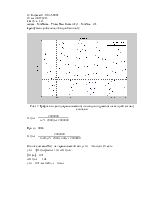
Рис.2. Диаграмма нулей и полюсов данного фильтра.
Из результатов вычисления видно, что система имеет два полюса с отрицательной вещественной частью (полюса находятся в левой полуплоскости) => система устойчива.
3) Выполнение разложения передаточной функции на простые (элементарные) дроби с использованием функции residue(). Запись этого разложения, используя выходные аргументы residue(). Получение импульсной характеристики фильтра, используя обратное преобразование Лапласа для найденного разложения. Построение графика импульсной характеристики.
Разложение передаточной функции на простые (элементарные) дроби с использованием функции residue():
b=[2000000];
a=[1 2000 2000000];
[r, p, k]=residue(b, a)
r =
1.0e+003 *
0 - 1.0000i
0 + 1.0000i
p =
1.0e+003 *
-1.0000 + 1.0000i
-1.0000 - 1.0000i
k =
[]
Т.к. степень полинома знаменателя больше, чем степень
полинома числителя, то целая часть их отношения равна 0, поэтому k = [] (пустая матрица). Система имеет пару
комплексно-сопряженных полюсов ![]() .
.
Запишем разложение, используя выходные аргументы residue():
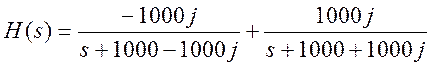
Получим импульсную характеристику фильтра:
Т.к. имеется пара комплексно-сопряженных полюсов ![]() , то импульсная характеристика равна
, то импульсная характеристика равна
![]()
![]()
Импульсную характеристику можно найти с помощью Matlab:
syms s;
h=(-1000*j)/(s+1000-1000*j)+(1000*j)/(s+1000+1000*j);
ilaplace(h)
ans =
-1000*i*exp((-1000+1000*i)*t)+1000*i*exp((-1000-1000*i)*t)
Далее представлен М-файл с помощью которого был получен график импульсной характеристики:
t=0:0.00001:0.006;
x=(-1000*j)*exp((-1000+1000*j).*t)+(1000*j)*exp((-1000-1000*j).*t);
figure(2),
plot(t,x),
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
title('График импульсной характеристики'),
xlabel('t'), ylabel('h(t)')
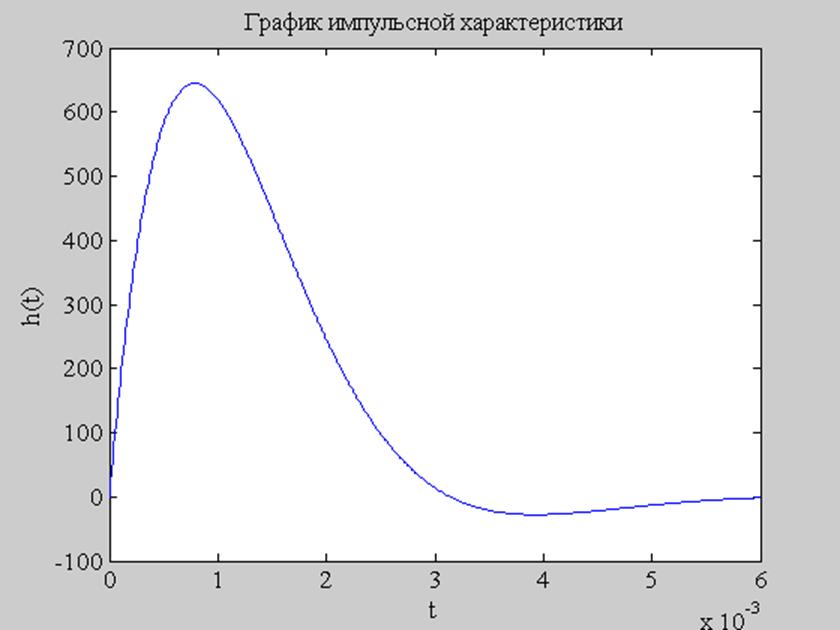
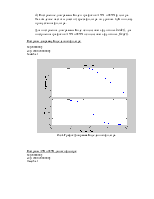
Рис.3. График импульсной характеристики данного фильтра.
4) Построение диаграммы Боде и графиков АЧХ и ФЧХ фильтра. Нахождение частоты (частот) среза фильтра по уровню 3дБ и полосу пропускания фильтра.
Для построения диаграммы Боде использовать функцию bode(), для построения графиков АЧХ и ФЧХ использовать функцию freqs().
Построим диаграмму Боде данного фильтра:
b=[2000000];
a=[1 2000 2000000];
bode(b,a)
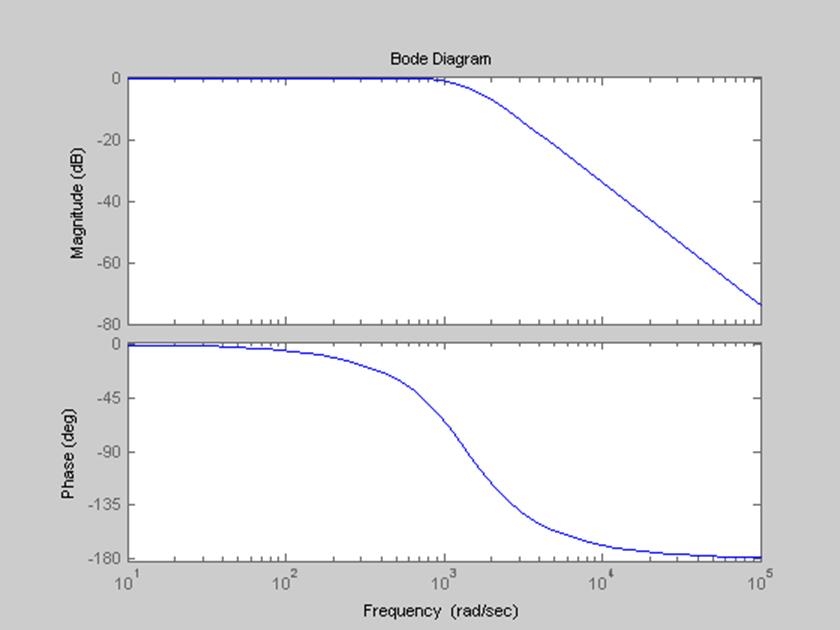
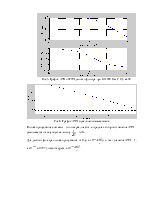
Рис.4. График Диаграмма Боде данного фильтра.
Построим АЧХ и ФЧХ данного фильтра:
b=[2000000];
a=[1 2000 2000000];
freqs(b,a)
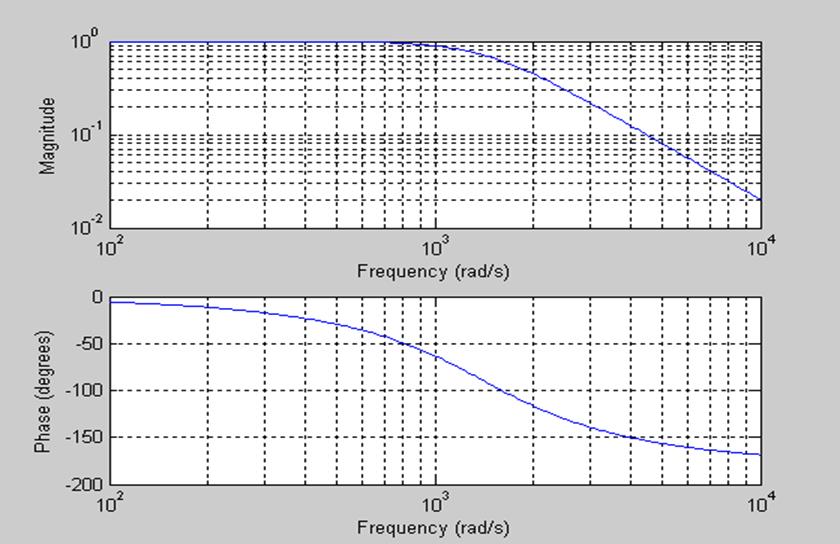
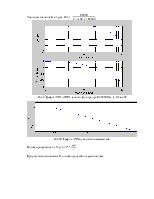
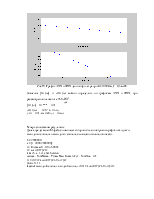
Рис.5. График АЧХ и ФЧХ данного фильтра при R=1000 Ом, С=0,5 мкФ.
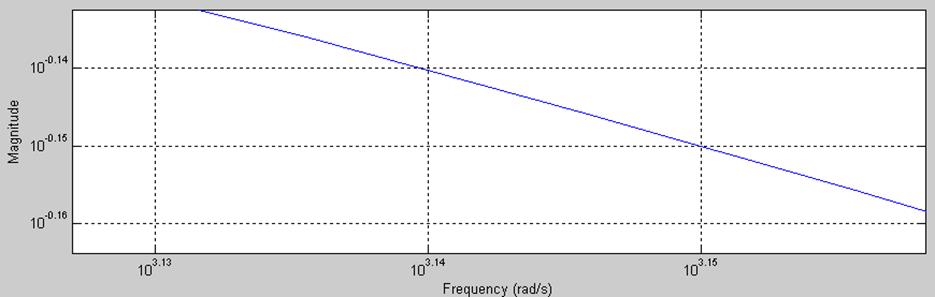
Рис.6. График АЧХ в увеличенном масштабе.
Полоса пропускания системы – это интервал частот, в пределах
которого значение АЧХ уменьшается на заданную величину 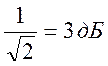 .
.
Для данного фильтра полоса пропускания от 0 до  (т.к. max значение АЧХ = 1, а
(т.к. max значение АЧХ = 1, а ![]() ),
частота среза
),
частота среза  .
.
5) Изменение значений параметров схемы (резисторов и конденсаторов), наблюдение за изменениями АЧХ, ФЧХ и полосы пропускания фильтра.
Уменьшим значение R
в 5 раз: 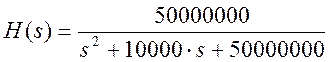
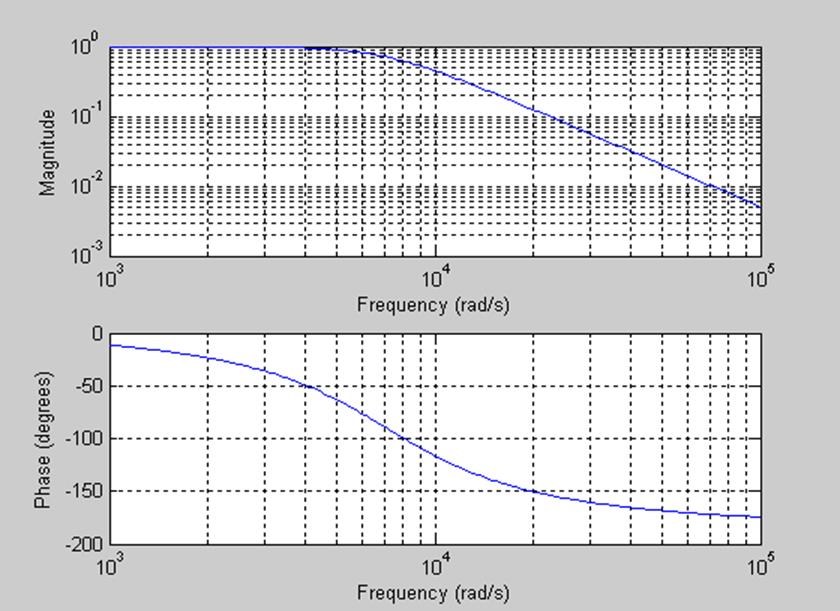
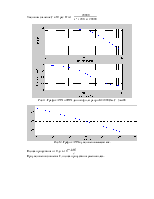
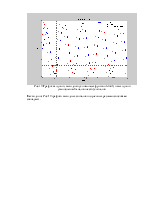
Рис.7. График АЧХ и ФЧХ данного фильтра при R=200 Ом, С=0,5 мкФ.
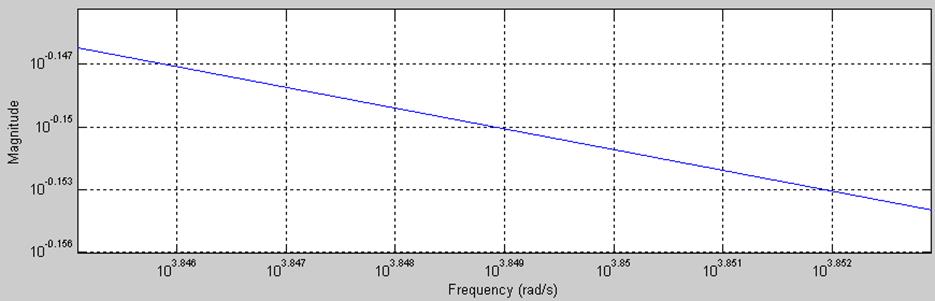
Рис.8. График АЧХ в увеличенном масштабе.
Полоса пропускания от 0 до 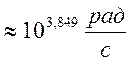
При уменьшении значения R, полоса пропускания увеличилась.
Увеличим значение R
в 5 раз: 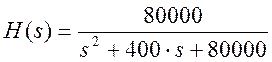
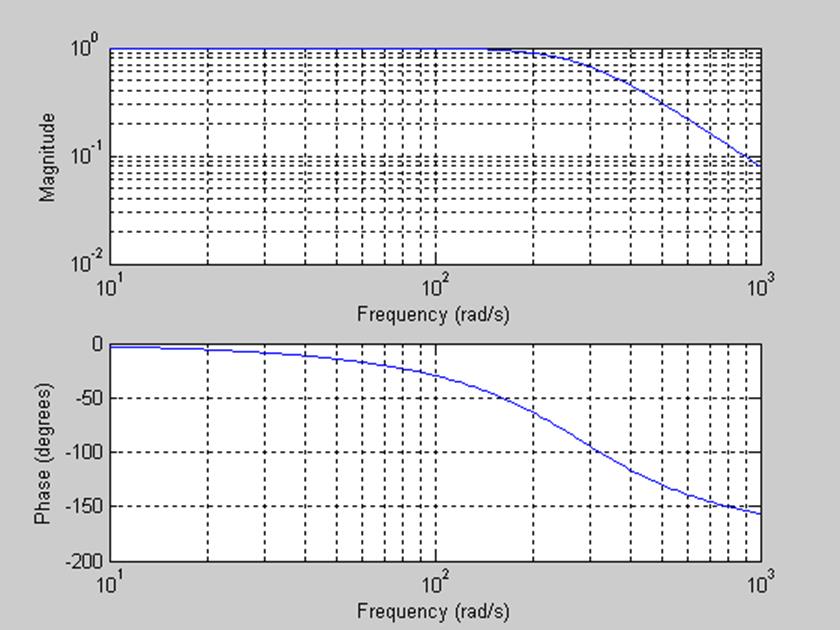
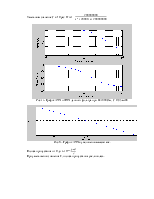
Рис.9. График АЧХ и ФЧХ данного фильтра при R=5000 Ом, С=0,5 мкФ.
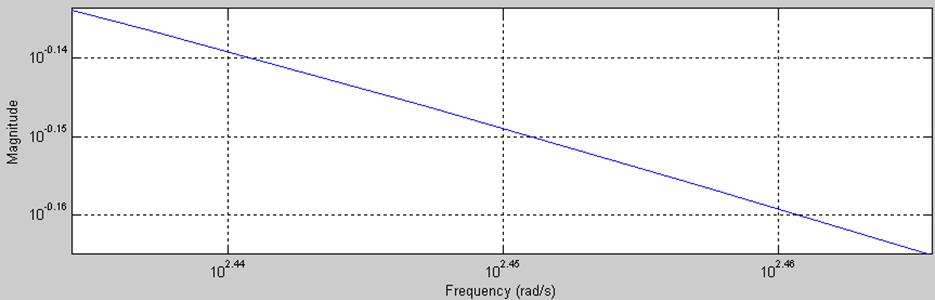
Рис.10. График АЧХ в увеличенном масштабе.
Полоса пропускания от 0 до 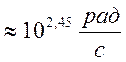
При увеличении значения R, полоса пропускания уменьшилась.
Увеличим значение С в 10 раз: 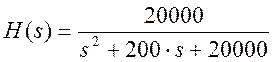
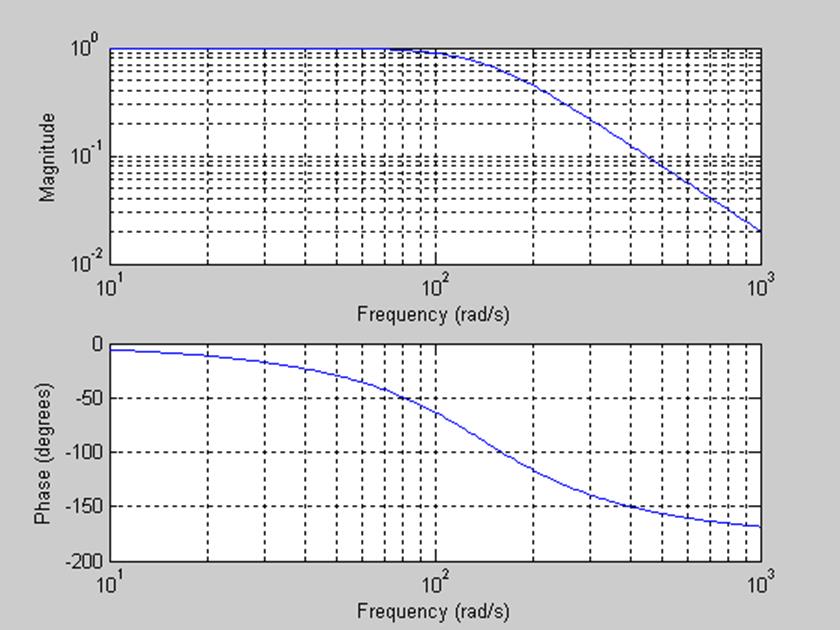
Рис.11. График АЧХ и ФЧХ данного фильтра при R=1000 Ом, С=5 мкФ.
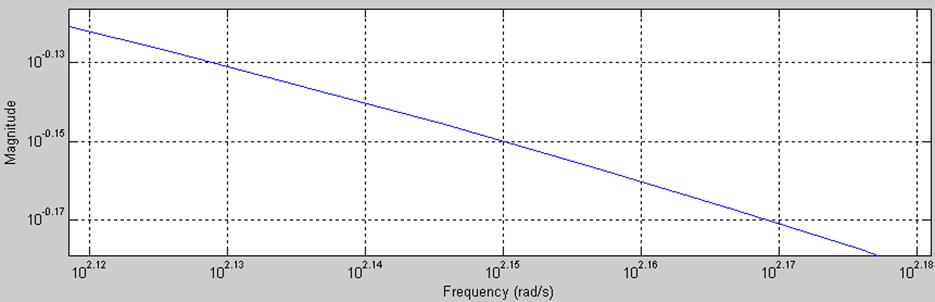
Рис.12. График АЧХ в увеличенном масштабе.
Полоса пропускания от 0 до 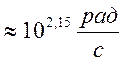
При увеличении значения C, полоса пропускания уменьшилась.
Уменьшим значение С в 10 раз: 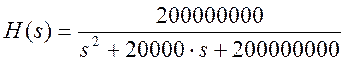
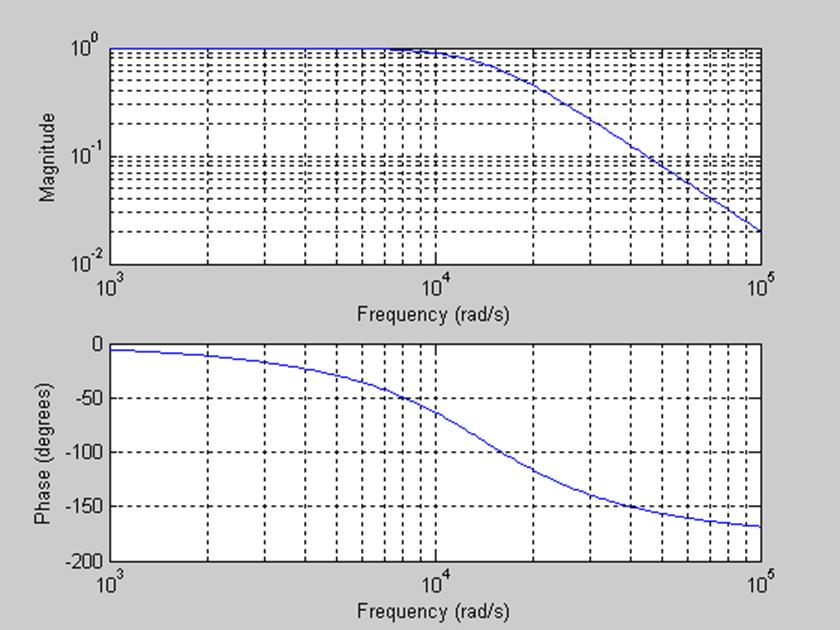
Рис.13. График АЧХ и ФЧХ данного фильтра при R=1000 Ом, С=0,05 мкФ.
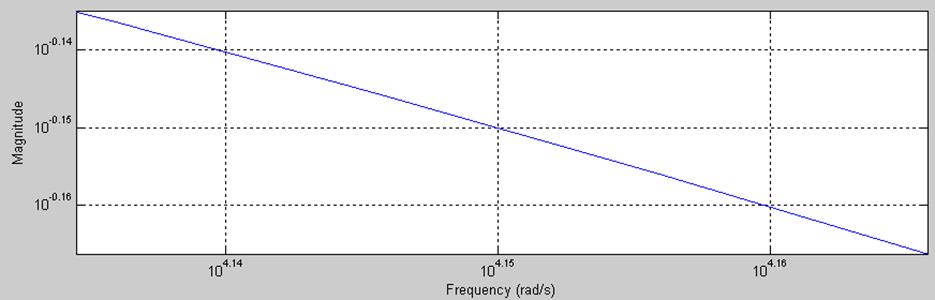
Рис.14. График АЧХ в увеличенном масштабе.
Полоса пропускания от 0 до 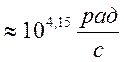
При уменьшении значения C, полоса пропускания увеличилась.
6)
Построение графиков переходной и импульсной характеристик фильтра. Получение выходного
сигнала фильтра для входного сигнала вида ![]() с
использованием функции conv.
с
использованием функции conv.
Для построения графиков использовать переходной и импульсной характеристик фильтраstep() и impulse().
b=[2000000];
a=[1 2000 2000000];
step(b,a)
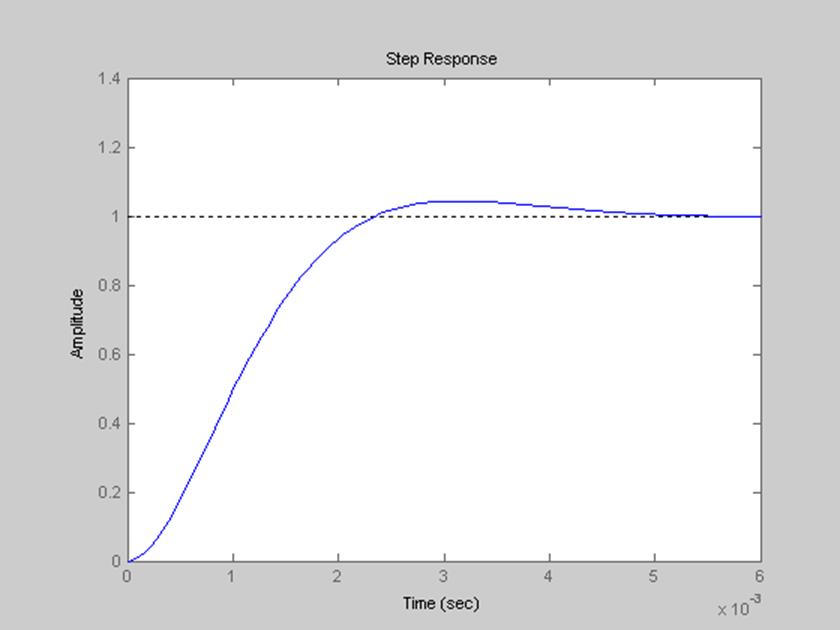
Рис. 15. График переходной характеристики данного фильтра.
b=[2000000];
a=[1 2000 2000000];
impulse(b,a)
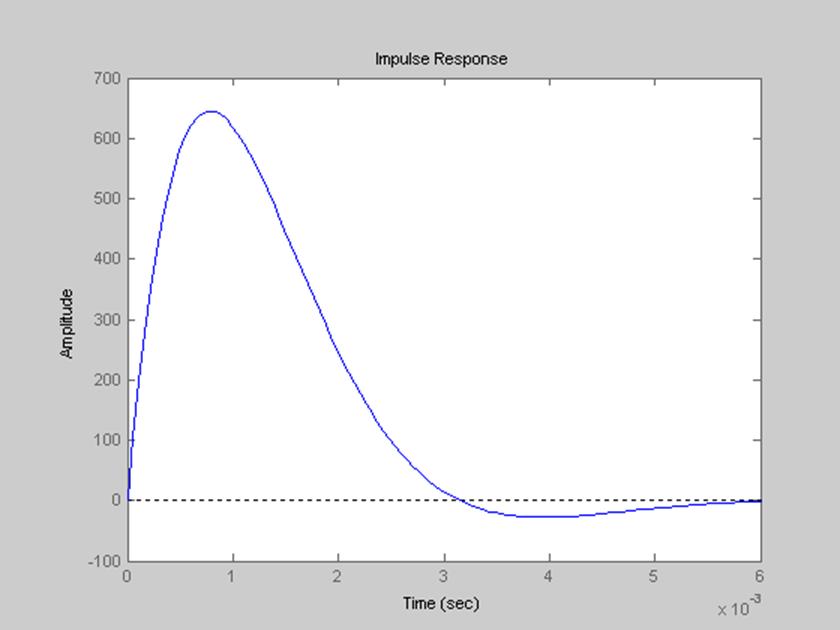
Рис. 16. График импульсной характеристики данного фильтра.
Переходная характеристика – реакция системы на входное воздействие в виде единичной ступенчатой функции при нулевых начальных условиях.
Импульсная характеристика – реакция системы на входной сигнал в виде δ-функции при нулевых начальных условиях.
7) Определение входного гармонического сигнала с частотой, входящей в полосу пропускания фильтра. Нахождение отклика (выходной сигнал) системы на данный входной сигнал. Построение графиков входного и выходного сигналов. Сделать аналитическую оценку выходного сигнала, базируясь на частотной характеристике системы и выражении для выходного сигнала в частотной области. Сопоставить результаты.
Для нахождения отклика (выходной сигнал) системы на данный входной сигнал использовать функцию lsim().
Далее представлен М-файл с помощью которого были построены графики входного и выходного сигнала.
b = 2000000;
a = [1 2000 2000000];
t = linspace (0 , 0.03, 5000);
f = cos (300*pi*t);
lsim (b, a, f ,t),
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
legend('выходной сигнал','входной сигнал');
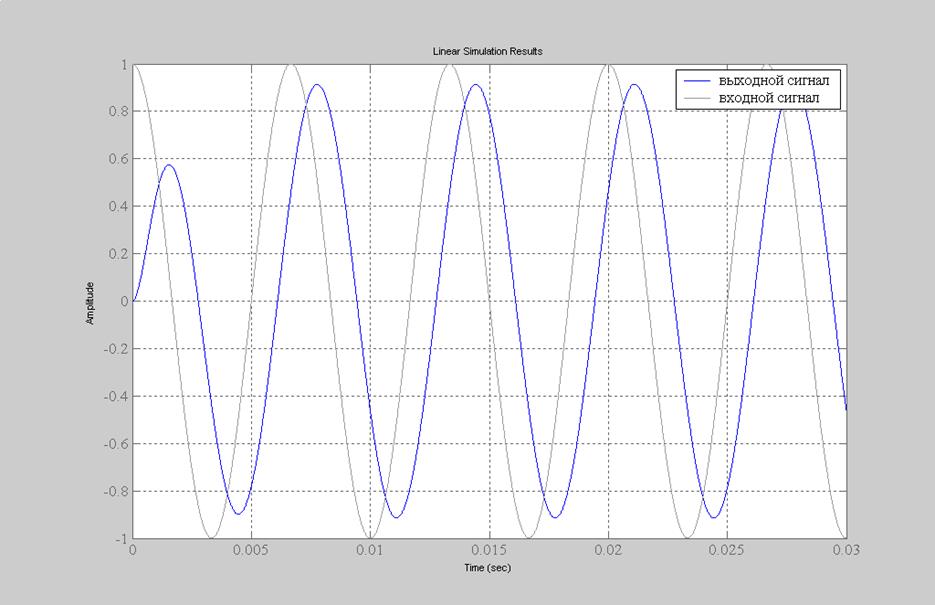
Рис.17. График входного (гармонического) и выходного (реакция на входной сигнал) сигналов.
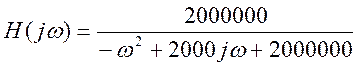
При ![]()
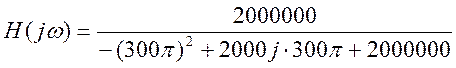
Отклик системы H(s) на гармонический вход ![]() есть
есть
![]() .
.
![]()
![]()
![]()
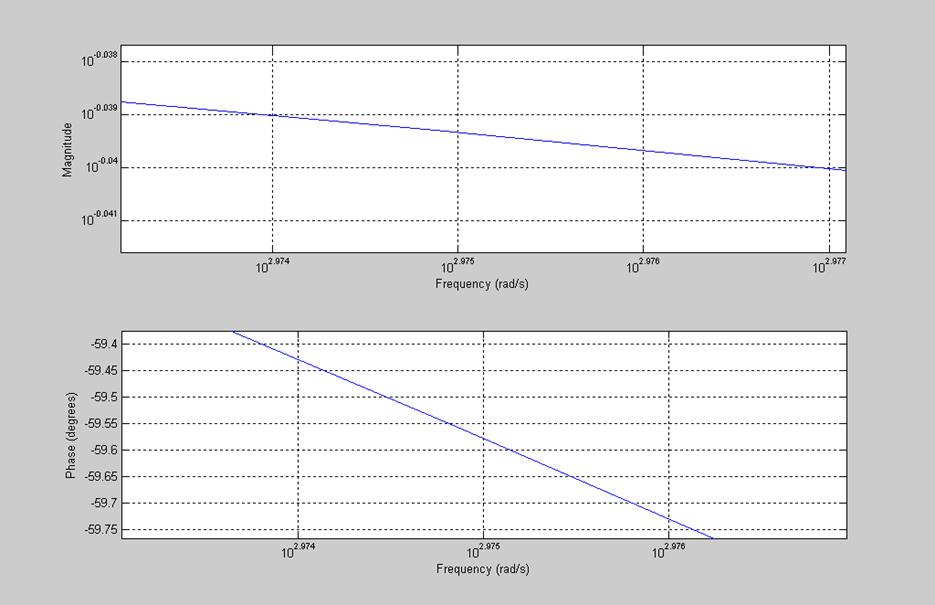
Рис.18. График АЧХ и ФЧХ данного фильтра при R=1000 Ом, С=0,5 мкФ.
Значения ![]() и
и
![]() можно определить по графикам АЧХ и
ФЧХ, при рассмотрении на частоте
можно определить по графикам АЧХ и
ФЧХ, при рассмотрении на частоте 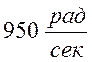 .
.
![]()
![]()
![]()
Теперь сопоставим результаты:
Далее представлен М-файл с помощью которого были построены графики входного, выходного сигнала и выходного сигнала, вычисленного аналитически.
b = 2000000;
a = [1 2000 2000000];
t = linspace (0 , 0.03, 5000);
f = cos (300*pi*t);
lsim (b, a, f ,t), grid, hold on,
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
f1 = (0.91)*cos(300*pi*t-0.33*pi);
plot(t,f1,'r'),
legend('выходной сигнал','входной сигнал','(0.91)*cos(300*pi*t-0.33*pi)');
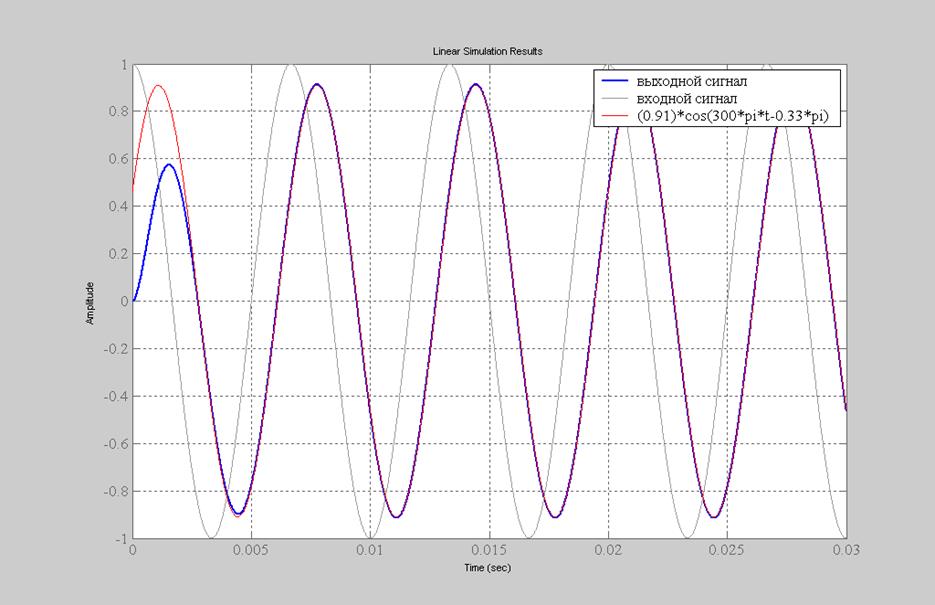
Рис.19. График входного, выходного (с помощью функции lsim()) и выходного (вычисленный аналитически) сигналов.
Как видно из Рис.19 графики выходных сигналов полученных разными способами совпадают.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.