Изображение спектра дискретного сигнала, определение наложения спектров

Задачи  5

1.  Гармоника   дискретизируется с частотами отсчетов

а)  ,     б)   . Изобразить спектр дискретного сигнала, определить, имеет ли место наложение спектров.

Решение.

Преобразование Фурье гармоники    .

Графики спектров

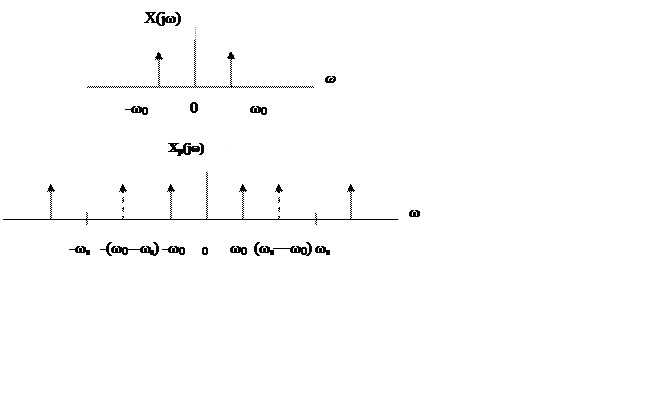а) 

Наложения спектров нет,  следовательно,  возможно восстановление исходного сигнала ФНЧ с частотой среза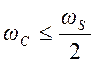 

б)   ,   график спектра дискретного сигнала

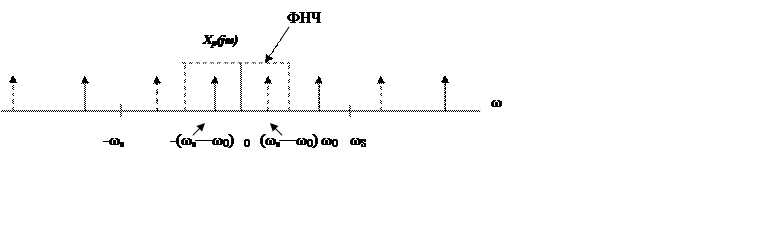
Нарушаются требования теоремы отсчетов,  восстановление гармоники с частотой ω₀ невозможно.

2.  Постройте примерные графики амплитудных спектров дискретных сигналов, получаемых идеальной дискретизацией ,  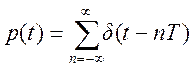 аналогового сигнала  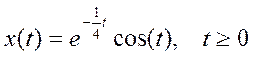с интервалами  отсчетов а)  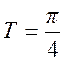 сек,   б)  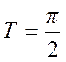сек,
в) 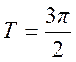 сек. Определите для каждого случая, происходит ли наложение спектров.
Решение.

            Спектральная плотность (комплексный спектр) сигнала

             

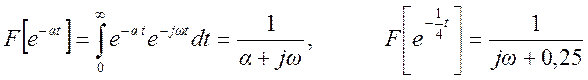
 По свойству частотного сдвига  преобразования Фурье      .

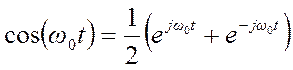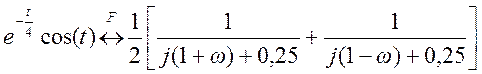По формулу Эйлера    ,  поэтому .        График спектра

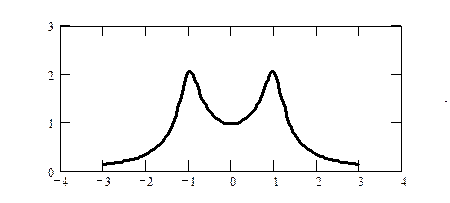
а) Дискретизация с интервалом 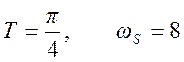        .      График спектра дискретного сигнала

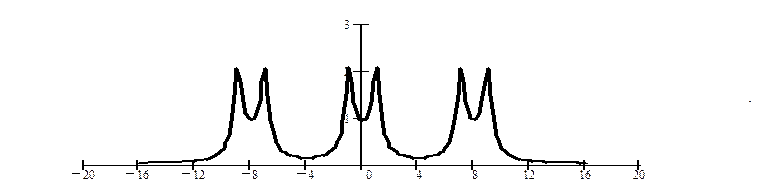
Имеются небольшие наложения спектров, обусловленные «хвостами» спектра непрерывного сигнала.

б) Дискретизация с интервалом 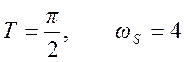        .      График спектра дискретного сигнала

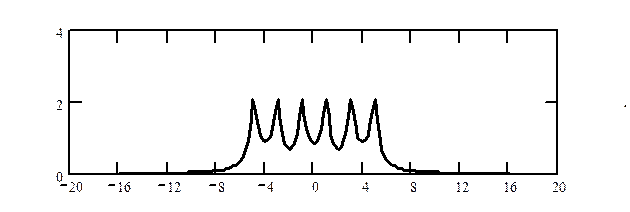
Наблюдается большее по сравнению с п. а) наложение спектров при дискретизации

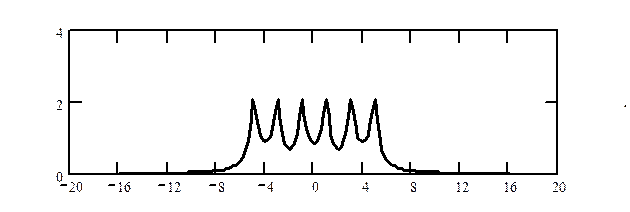
в) Дискретизация с интервалом 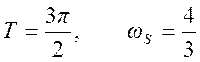        .      График спектра дискретного сигнала

Происходит явное наложение и искажение спектра основной полосы из-за нарушения требований теоремы отсчетов.

3.  Предположим следующую модель дискретизации и восстановления сигналов

          Для получения выходного сигнала y(t) дискретный сигнал ,  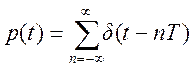пропускается через идеальный ФНЧ с частотной характеристикой

Для аналогового сигнала  и интервала отсчетов Т = 0,01 сек.
а) изобразите амплитудный спектр исходного аналогового сигнала и дискретного сигнала . Объясните, происходит ли в этом случае наложение спектров?
б) запишите выражение для y(t),

в) определите выражение для x[n],

г)  определите, будет ли наложение спектров при  Т =0,025 сек.

Решение.

а)  Преобразование Фурье константы (см. уч.пособие Г&Щ,    ТОС, ч.1, стр. 55 -56)

.

Преобразование Фурье гармоники

.

Поэтому  .   Графики амплитудного спектра аналогового и дискретного с интервалом  Т = 0, 01 сек сигнала. Угловая частота отсчетов .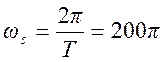

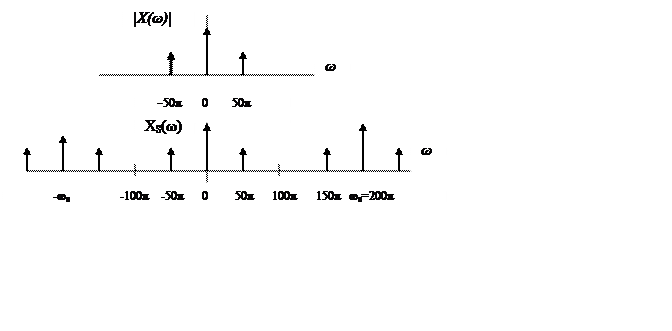
б)  В этом случае наложения спектров нет,  сигнал, восстановленный идеальным ФНЧ  с частотой среза 

в)  вид дискретного сигнала  

г)  Вид амплитудного спектра дискретного сигнала при дискретизации с частотой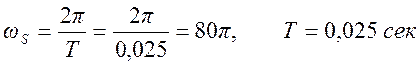

При дискретизации с частотой  80π  происходит наложение спектров, в полосу частот восстанавливающего  фильтра  ± 40π попадает гармоника с частотой 30π  (aliasing !)   и выходной сигнал восстанавливающего фильтра будет иметь вид   .

4. 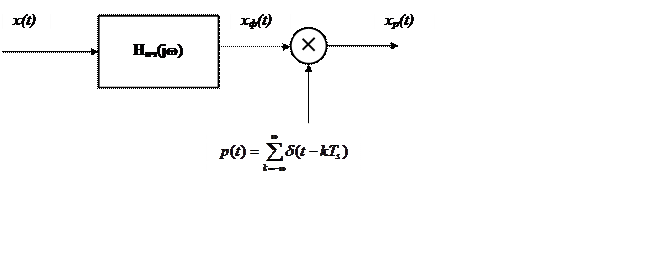 На рис. показана  система дискретизации, состоящая из предфильтра (фильтр нижних частот для устранения наложения спектров, частотная характеристика H_нч(jω)) и идеального амплитудно-импульсного модулятора (АИМ)











Пусть входной сигнал имеет вид 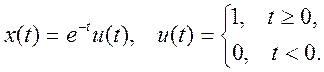        Интервал отсчетов  равен   .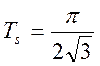 
Найти преобразование Фурье (спектр) входного сигнала. Какова должна быть частота среза предфильтра? Какая часть энергии сигнала  попадает в полосу пропускания предфильтра?
Решение.
Преобразование Фурье входного сигнала x(t)

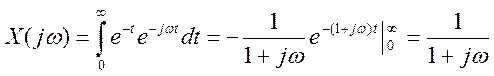
График амплитудного спектра входного сигнала

 

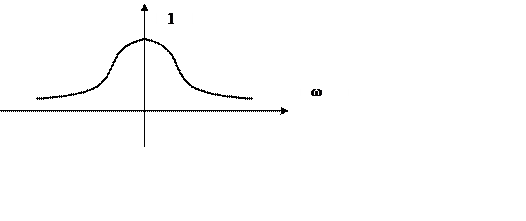            Частота среза предфильтра  должна быть по крайней мере .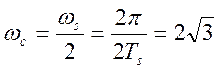

График спектра дискретного сигнала

 

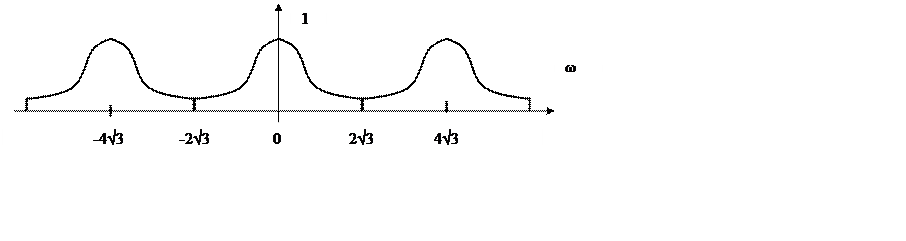
Полная  энергия входного сигнала

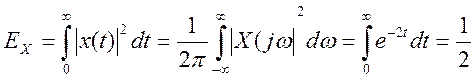
Энергия на выходе идеального предфильтра

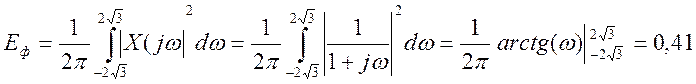
Относительная часть энергии сигнала на выходе фильтра

.

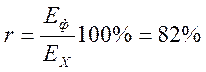Следовательно, при данных условиях по  меньшей мере 18% энергии сигнала просачивается в основную полосу. Для снижения этой доли нужно повысить частоту дискретизации и частоту среза предфильтра.

5.  Максимальное значение  двоичного 10 – разрядного аналого – цифрового преобразователя равно 10 В. Определить шаг квантования в абсолютных единицах и в процентах от предельного значения сигнала, а также максимальное и  среднеквадратичное значение  погрешности квантования по уровню. 
Решение.

Число уровней квантования  , следовательно, шаг квантования равен

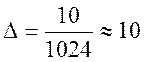 мВ, что составляет  ≈ 0,1% от максимального значения сигнала.

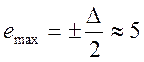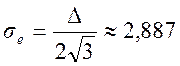Максимальная погрешность квантования по уровню равна  мВ, её среднеквадратичное значение   мВ.

6. 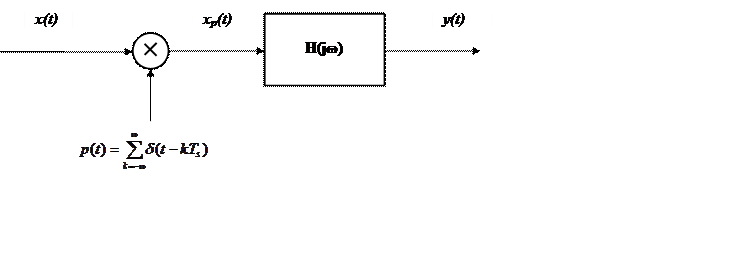 При восстановлении непрерывного сигнала по отсчетам они пропускаются через идеальный ФНЧ с частотной характеристикой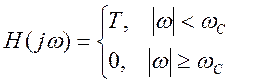 

Пусть частота отсчетов   ,   граничная частота спектра , частота среза  ФНЧ      .  

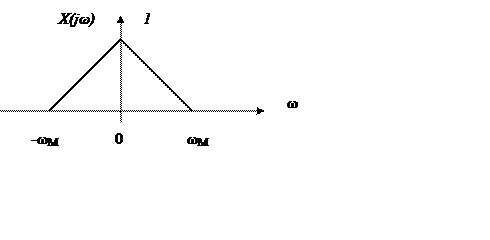
Спектр (преобразование Фурье)  исходного сигнала x(t)

 

Найти отношение части энергии сигнала, обусловленной наложением спектров, к  полной энергии сигнала y(t).

       Решение.

Интервал отсчетов  .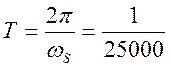

Спектр  сигнала после дискретизации

 

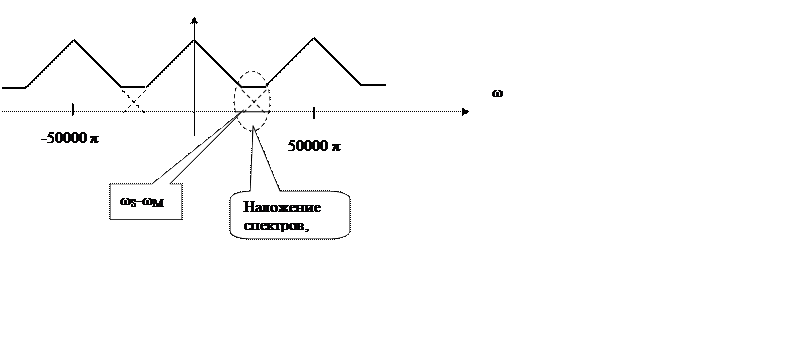Вид  основной полосы спектра  дискретного сигнала

 

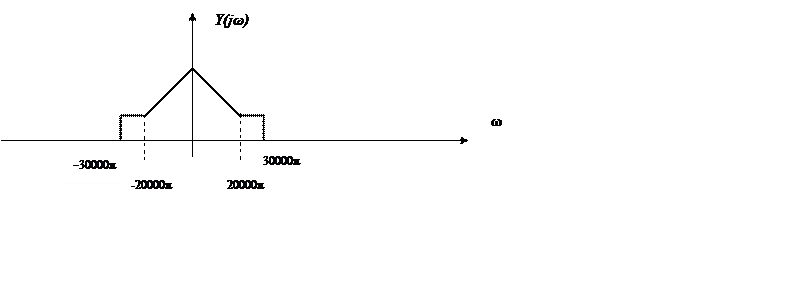Часть энергии, содержащейся в неискаженной части основной полосы 

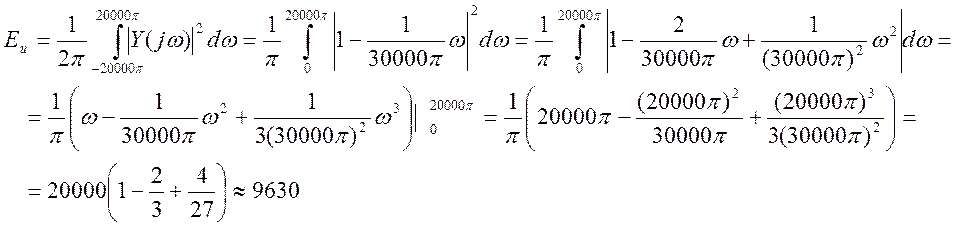Часть энергии, содержащейся в полосе наложения спектров (

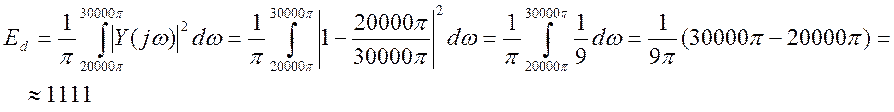
 Относительная доля энергии в области наложения спектров

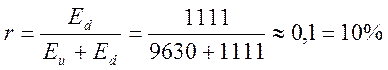
7.  Пусть сигнал 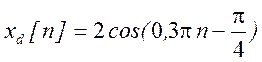 получен при частоте отсчетов Fs = 6000 Гц. Каким различным аналоговым гармоникам с частотами ниже 8000 Гц соответствует ?
            Решение.

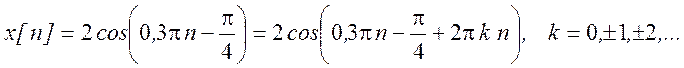
Для k = 0 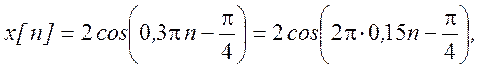 нормализованная частота

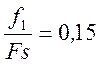.   Отсюда Гц.   Следовательно, первая из искомых гармоник   .

Вторая гармоника соответствует  k = 1

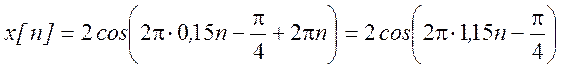.   При этом аналоговая частота

Гц и .

8.  Двухканальная (стереофоническая) пятнадцатибитная цифровая акустическая система имеет частоту отсчетов в каждом канале, равную 48,2 кГц. Определить частоту передачи данных в бит / сек.

Решение.

            Для обеспечения частоты отсчетов 48,2 кГц на канал суммарная частота отсчетов должна составлять 2 ∙ 48,2 = 96,4 кГц. Каждый отсчет квантуется 15 – битным преобразователем, при этом каждый отсчет сигнала представляется последовательностью из 15 бит. Следовательно, общая скорость передачи данных будет составлять 
15 ∙ 96400 = 1,446 Мбит/сек.

9.  Телевизионный сигнал черно – белого телевидения  состоит из 600 строк по 650 элементов в строке при частоте кадров  30 кадр / сек. Определить полосу частот и минимально необходимую частоту отсчетов телевизионного сигнала.

Решение. 

            Количество элементов яркости телевизионного сигнала, передаваемых за 1сек.,  при условиях задачи составляет  N = 625 ∙ 600 ∙ 30 = 11250000 эл/сек.  Минимально необходимый интервал отсчетов должен удовлетворять условию 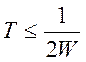, где W – полоса частот телевизионного сигнала.  Отсюда 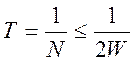    или 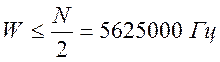.  Таким образом полоса частот видеосигнала при данных условиях составляет 5,625 МГц  и частота отсчетов 11,25 МГц.

Задачи для самостоятельного решения

1.  Сигнал   подвергается дискретизации с частотой отсчетов  . Запишите выражение дискретного сигнала.
Ответ:  .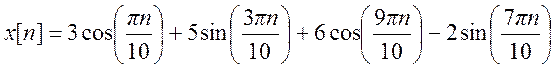

2.   Изобразите графики амплитудных спектров дискретного сигнала  для модели идеальной дискретизации ,  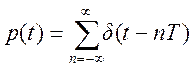  с периодом отсчетов    
а) 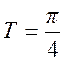  сек,       б)  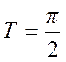сек,     в)  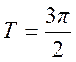сек.
 Амплитудный спектр аналогового сигнала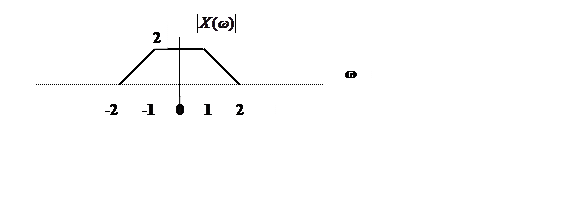

Определите, в каких случаях имеется наложение спектров.

Ответ:  а) 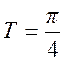  ,   нет  наложения спектров,  б) 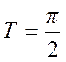 ,  граничный случай,

              в) 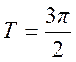   ,  происходит наложение спектров.

3.     Сигнал  x(t)  со спектральной плотностью    дискретизируется  с  интервалом отсчетов, равным  100 мкс. Возможно ли полное восстановление сигнала по его отсчетам?

Ответ.  Невозможно.

4.  Модель дискретизации и восстановления сигналов:

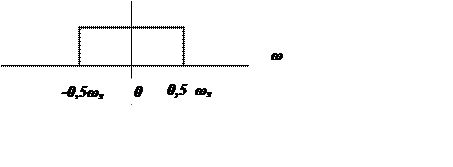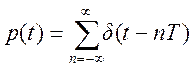          Для получения выходного сигнала y(t) дискретный сигнал ,  пропускается через идеальный ФНЧ с частотной характеристикой

Пусть  , интервал отсчетов  Т = 0,1 сек.  Постройте график спектра дискретного сигнала , найдите выражение для  .

Ответ: 

5.   Повторите схему задачи п.3  для аналогового сигнала  и интервала отсчетов Т = 0,01 сек,  постройте  амплитудный спектр исходного аналогового сигнала и дискретного сигнала . Происходит ли в этом случае наложение спектров?

Ответ:  имеется наложение спектров, восстановленный сигнал имеет вид

6.  Определите минимальную частоту отсчетов, необходимую для дискретизации сигнала  .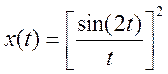

Ответ.  или  .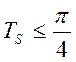

Указание.  Обратите внимание, что сигнал во временной области можно представить как произведение двух функций вида 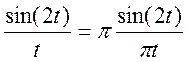 . В частотной области такой функции соответствует преобразование Фурье 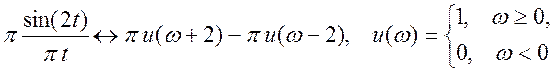 .  Произведению функций во временной области соответствует  свертка преобразований Фурье в частотной области, в данном случае  свертка двух прямоугольных функций,  дающая треугольную функцию.

7.  Сигнал x(t)  имеет синусоидальные компоненты с частотами  f₁ = 250,  f₂ = 450, 
f₃ = 1000 Гц. Этот сигнал преобразуется в дискретный с частотой отсчетов  F_S = 1,5 кГц. После дискретизации сигнал восстанавливается  с помощью ФНЧ с частотой среза 750 Гц. Определите частотные компоненты восстановленного сигнала.

Ответ: в  выходном сигнале будут присутствовать синусоидальные составляющие с частотами  250,   450,  500 Гц.

8.  Монитор компьютера имеет разрешение 800*600 пиксел при частоте кадров 70 Гц. Определите максимальную частоту и минимально необходимую частоту отсчетов видеосигнала.

Ответ:  16,8 МГц,   33,6 МГц.