






МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
ЛАБОРАТОРНАЯ РАБОТА № 8
по дисциплине
«Теория и обработка сигналов»
Выполнили:
Студентки
Факультета АВТ
Группы АО-21
Рогова Татьяна
Яшина Оксана
Преподаватель:
Доц. Ю. И. Щетинин
Новосибирск
2005
Z - преобразование
и дискретно – временное преобразование Фурье
Цель работы:Изучение Z – преобразования и дискретно – временного преобразования Фурье (ДВПФ), их вычисления в среде Matlab.
1. Прямое и обратное Z-преобразование:
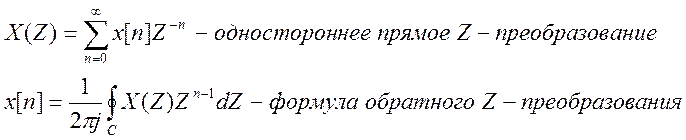
Z-преобразование широко используется при анализе и проектировании дискретных систем. Для дискретных систем оно играет ту же роль, что и преобразование Лапласа для непрерывных систем. Прямое Z-преобразование:
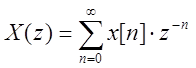
Последовательности x(n) с помощью Z-преобразования ставится в соответствие функция X(z) комплексной переменной z.
Возможность нахождения последовательности x(n) по её Z-преобразованию X(z) следует из теории функций комплексной переменной.
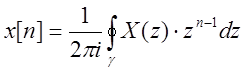
Интегрирование производится в плоскости z
по контуру ![]() , содержащему внутри себя все полюсы
функции X(z).
, содержащему внутри себя все полюсы
функции X(z).
Аналитическое вычисление Z – преобразования сигналов:
а)
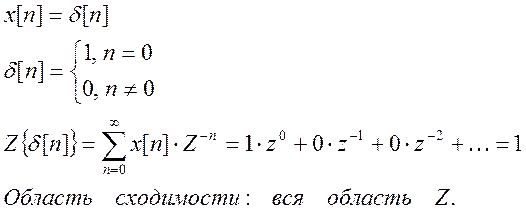
б)
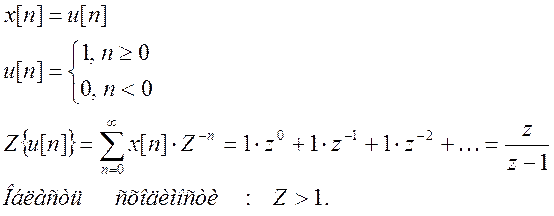
в)
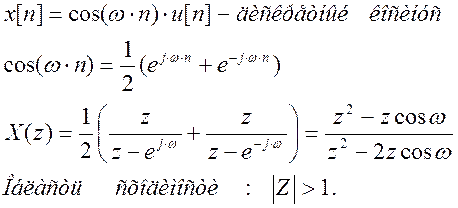
2. Нахождение в замкнутой форме Z – преобразования сигналов (последовательностей) с помощью функции ztrans() Matlab.
а) x[n] = an cos ωn
syms X x a w n
x=a^n*(cos(w*n));
X=ztrans(x)
>> vi4islenie1
X =
(z/a-cos(w))*z/a/(z^2/a^2-2*z/a*cos(w)+1)
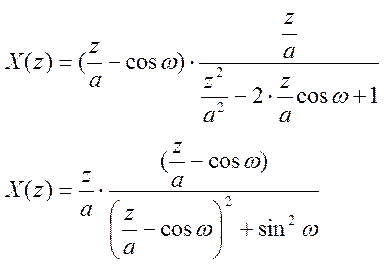
б) x[n] = n2e2n
syms X x n
x=n^2*(exp(2*n));
X=ztrans(x)
>> vi4islenie2
X =
z*exp(2)*(z+exp(2))/(z-exp(2))^3
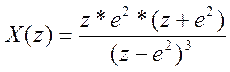
в) x[n] = cos2n
syms X x n
x=cos(n)^2;
X=ztrans(x)
>>vi4islenie3
X =
(z^2+z-3*z*cos(1)^2+cos(1)^2)*z/(z^3+z^2-4*z^2*cos(1)^2-z+4*z*cos(1)^2-1)
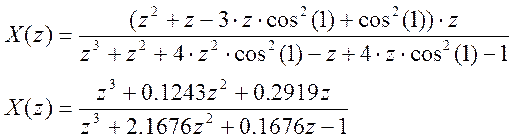
3. Определение сигнала во временной области (оригинал) по его Z – преобразованию, используя функцию iztrans() Matlab.
а) 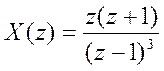
syms z x X
X=z*(z+1)/(z-1)^3;
x=iztrans(X)
>>vi4islenie4
x =
n^2
Таким образом, ![]()
б) 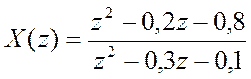
syms z x X
X=(z^2-0.2*z-0.8)/(z^2-0.3*z-0.1);
x=iztrans(X)
>>vi4islenie5
x =
8*charfcn[0](n)-36/7*(-1/5)^n-13/7*(1/2)^n
charfcn[0] – дельта-функция, где ненулевое значение только в точке равной нулю.
Таким образом, 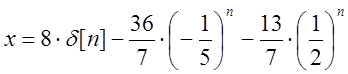
4. Разложение функции рационального Z – преобразования на простые дроби. с помощью функции residuez(). Используя это разложение, аналитическое вычисление обратного Z - преобразования.
Функция [r, p, k]=residuez(num, den) выполняет разложение на простые дроби рациональной Z- функции с вектором коэффициентов полинома числителя num и вектора коэффициентов полинома знаменателя den. Результат функции: r – вектор вычетов, p – вектор полюсов, k – вектор коэффициентов целой части разложения.
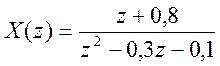
Разложение на простые множители:
Num=[1 0.8];
Den=[1 -0.3 -0.1];
[R,P,K] = RESIDUEZ(Num,Den)
>>razlozhenie
R =
3.7143
4.2857
P =
0.5000
-0.2000
K =
-8
Полученному результату отвечает разложение на простые дроби вида:
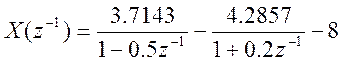
Обратное Z-преобразование:
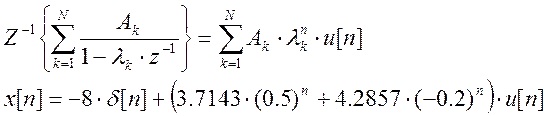
Данный пример иллюстрирует возможность перехода от Z-преобразования X(z) к последовательности x[n] во временной области с применением разложения X(z) на простые дроби. Заметим, что использование MatLab помогает значительно упростить процесс получения дробей, а, следовательно, снизить временные затраты.
5. Решение с помощью Z– преобразования линейного разностного уравнения с постоянными коэффициентами.
Уравнение ![]() .
.
Беря Z- преобразование от
уравнения, с учетом свойства временного сдвига получаем ![]() .
.
Z – преобразование входного
сигнала ![]() .
.
Отсюда ![]() .
.
Решение в Z – области
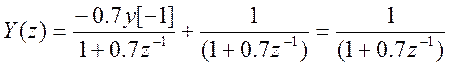
Обратное Z-преобразование от первого слагаемого правой части
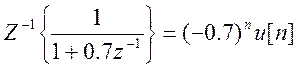 .
.
Проверка:
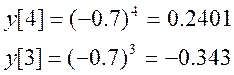
Подставим теперь эти значения в выражение:
![]()
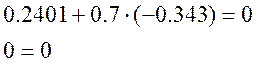
Проверка показала, что решение правильное.
6. Выражения прямого и обратного ДВПФ. Связь между ДВПФ и Z – преобразованием.
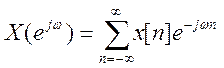 -
выражение прямого ДВПФ
-
выражение прямого ДВПФ
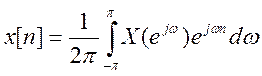 -
выражение обратного ДВПФ
-
выражение обратного ДВПФ
Прямое дискретно-временное преобразование Фурье:
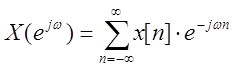
В данном выражение дискретному сигналу x[n] ставится в соответствие непрерывная функция ![]() , с переменной
, с переменной ![]() , представляющая собой ряд Фурье.
Коэффициенты ряда можно найти воспользовавшись обратным ДВПФ:
, представляющая собой ряд Фурье.
Коэффициенты ряда можно найти воспользовавшись обратным ДВПФ:
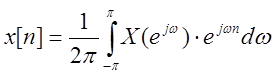
Связь ДВПФ и Z-преобразования обусловлена тем, что z является комплексной переменной:
![]()
![]()
подставив её в выражение ДВПФ при условии, что ![]() отличен от нуля только в
положительной полуплоскости, то получим:
отличен от нуля только в
положительной полуплоскости, то получим:
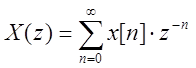 .
.
Очевидно, что ДВПФ – это частный случай Z-преобразования на единичной окружности комплексной z-плоскости.
Аналитическое вычисление ДВПФ сигнала
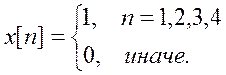
![]()
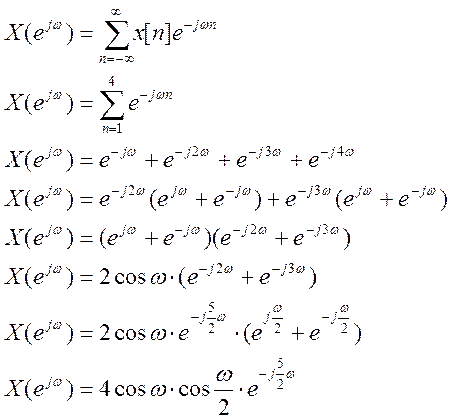
7. Вычисление дискретно-временного преобразования Фурье сигналов
а) x[n]
= e -0,5n,
б) 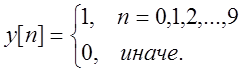
для значения M = 64.
Файл функция:
function [X,w] = DTFT(x,M)
% Функция вычисляет значения DTFT от вектора x.
% Обращение
% [X,w] = DTFT(x,0)
% здесь X - вектор значений DTFT,
% w - вектор угловых частот.
% Если желательно вычислить DTFT с M значениями частоты, используется обращение
% [X,w] = DTFT(x,M)
% Этот вариант используется, когда размер вектора x меньше размера вектора частот w,
% при этом x дополняется нулевыми значениями
N = max(M,length(x));
% Приведение FFT к размеру 2^m
N = 2^(ceil(log(N)/log(2)))
% Вычисление fft
X = fft(x,N);
% Вектор частот
w = 2*pi*( (0:(N-1))/N );
w = w - 2*pi*(w>=pi)
% Сдвиг FFT к интервалу от -pi до +pi
X = fftshift(X);
w = fftshift(w);
Построим графики амплитудного и фазового спектров этих сигналов:
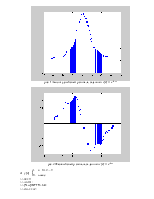
а) x[n] = e -0,5n
>> n=0:1:5;
>> x=exp(-0.5*n);
>> [X,w]=DTFT(x,64)
>> t=-31:1:32;
>> stem(t,abs(X))
>> stem(t,angle(X))
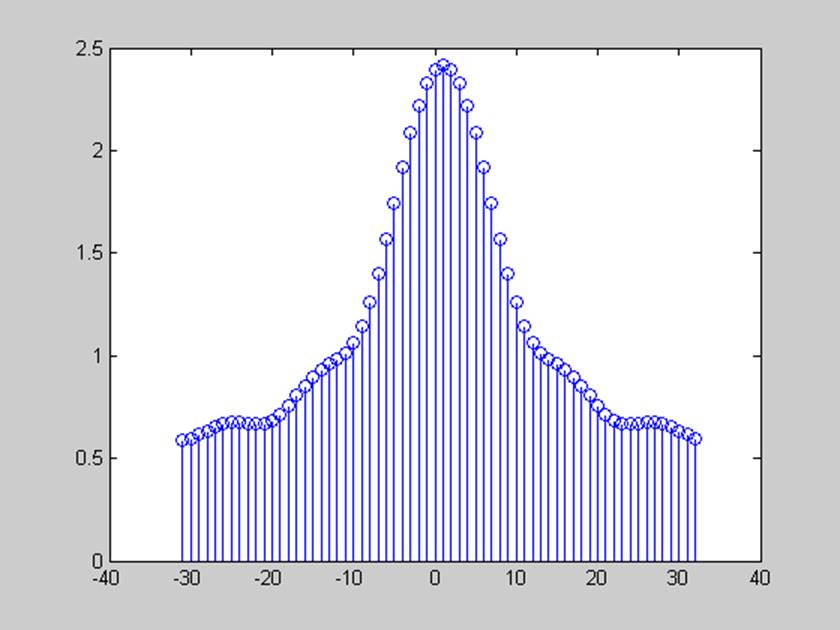
рис. 1 Амплитудный спектр сигнала, заданного x[n] = e -0,5n
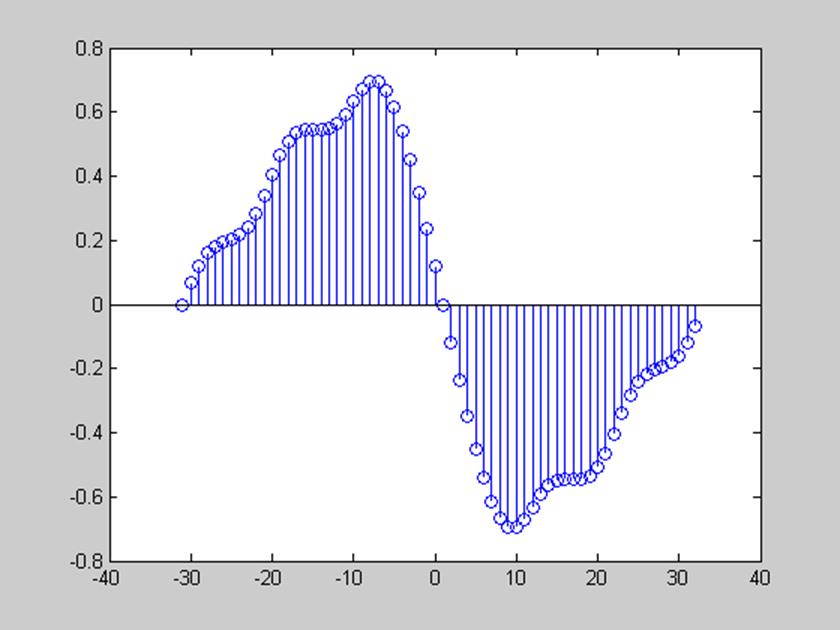
рис. 2 Фазовый спектр сигнала, заданного x[n] = e -0,5n
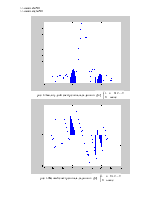
б) 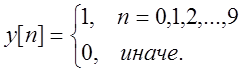
>> n=1:9;
>> x(n)=1;
>> [X,w]=DTFT(x,64);
>> t=-31:1:32;
>> stem(t,abs(X))
>> stem(t,angle(X))
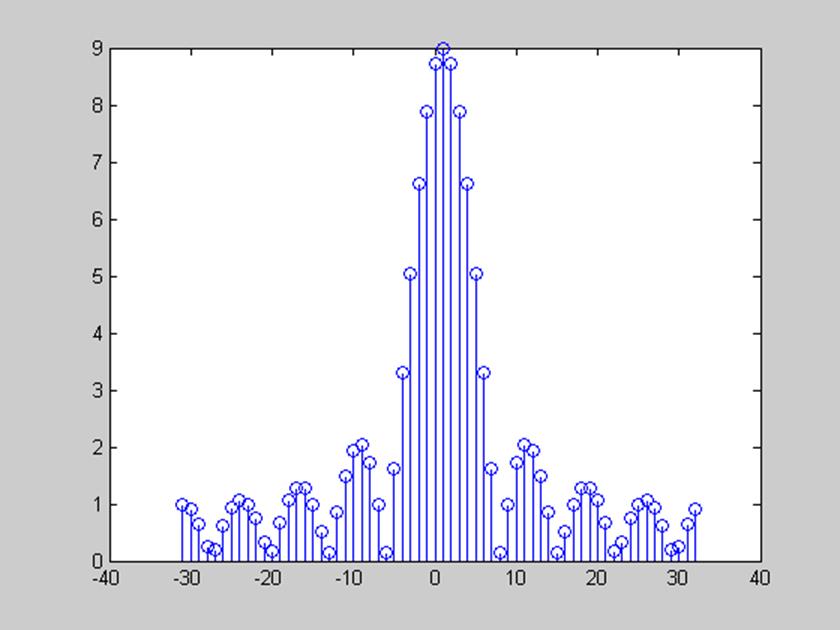
рис. 3 Амплитудный
спектр сигнала, заданного 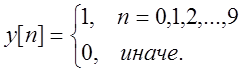
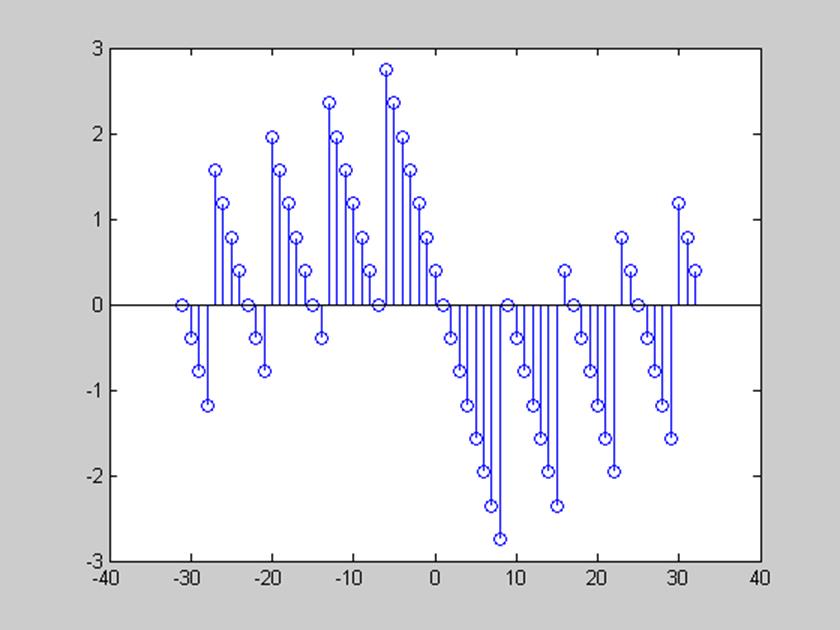
рис. 4 Фазовый спектр
сигнала, заданного 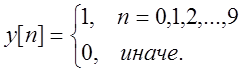
8.
Получите частотную характеристику дискретной системы с уравнением 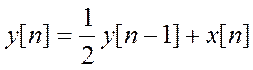 как отношение
как отношение 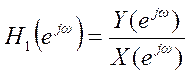 .
.
Найдем ДВПФ уравнения, учитывая свойства линейности и временного сдвига:
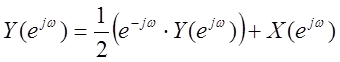
Тогда:
![]()
Откуда:
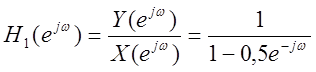
Найдем частотную характеристику инверсной системы ![]() такой, что последовательное
соединение этих систем имеет единичную частотную характеристику, т.е.
такой, что последовательное
соединение этих систем имеет единичную частотную характеристику, т.е. ![]() :
:
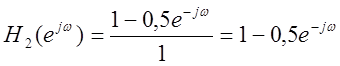
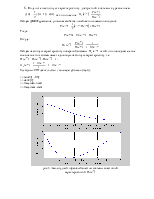
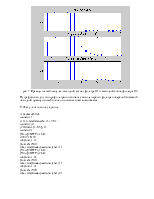
Построим АЧХ обеих систем с помощью функции freqz():
>> num=[1 -0.5];
>> den=[1];
>> freqz(den, num)
>> freqz(num, den)
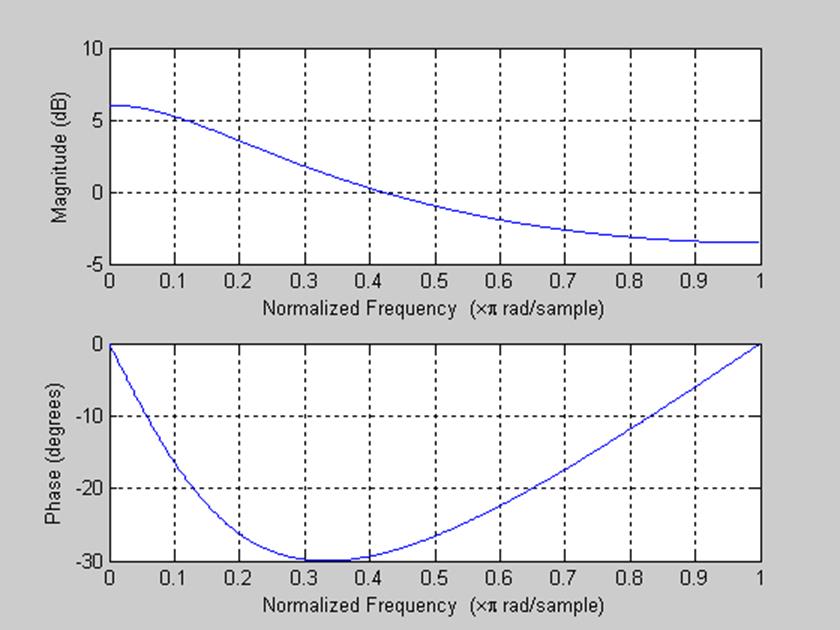
рис. 5 Амплитудный и фазовый спектры системы с частотной
характеристикой ![]()
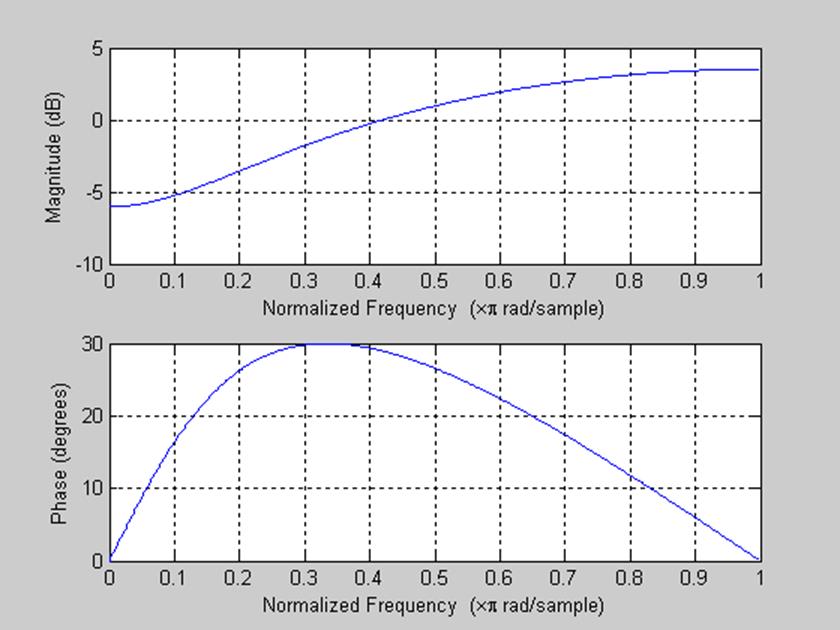
рис. 6 Амплитудный и фазовый спектры системы с частотной
характеристикой ![]()
Пронаблюдаем особенности работы системы. Для этого
сгенерируем прямоугольный импульс на интервале ![]() с
помощью функции rectpuls(). Используя функцию filter() проведем фильтрацию прямоугольного импульса
вначале системой (фильтром)
с
помощью функции rectpuls(). Используя функцию filter() проведем фильтрацию прямоугольного импульса
вначале системой (фильтром) ![]() , а затем ее
выход – системой
, а затем ее
выход – системой ![]() .
.
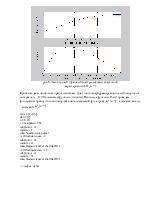
num = [1 -0.5];
den = [1];
n = 0:20;
x = rectpuls(n, 20);
subplot(3,1,1)
stem(n, x)
title('Square-wave pulse')
x1=filter(den, num, x);
subplot(3,1,2)
stem(n, x1)
title('Output signal of the filter H1')
x2=filter(num, den, x1);
subplot(3,1,3)
stem(n, x2)
title('Output signal of the filter H2')
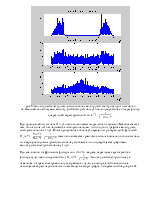
>> output_signal
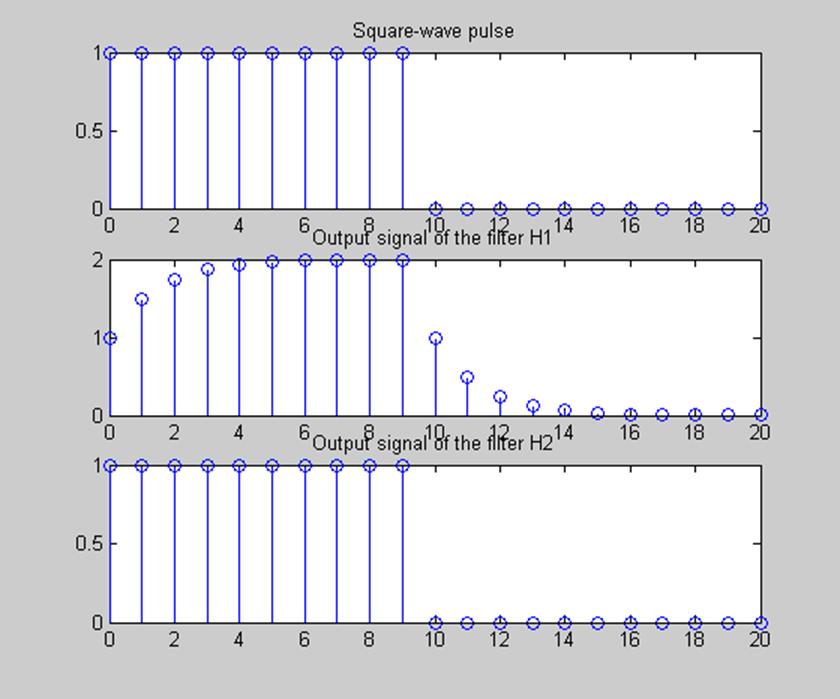
рис. 7 Прямоугольный импульс, выходной сигнал фильтра Н1 и выходной сигнал фильтра Н2.
Из графиков видно, что при фильтрации сигнала с выхода первого фильтра инверсной системой исходный прямоугольный сигнал полностью восстанавливается.
9. Факультативное задание
x1=auread('bird');
sound(x1)
y1=x1+randn(length(x1), 1)*0.1;
sound(3*y1)
y2=filter(1,[1 -0.5],y1);
sound(y2)
[X1,w]=DTFT(x1,64);
t=-8191:8192;
subplot(3,1,1)
plot(t,abs(X1))
title ('Amplitude spectrum signal x1')
[Y1,w]=DTFT(y1,64);
[Y2,w]=DTFT(y2,64);
subplot(3,1,2)
plot(t,abs(Y1))
title ('Amplitude spectrum signal y1')
subplot(3,1,3)
plot(t,abs(Y2))
title ('Amplitude spectrum signal y2')
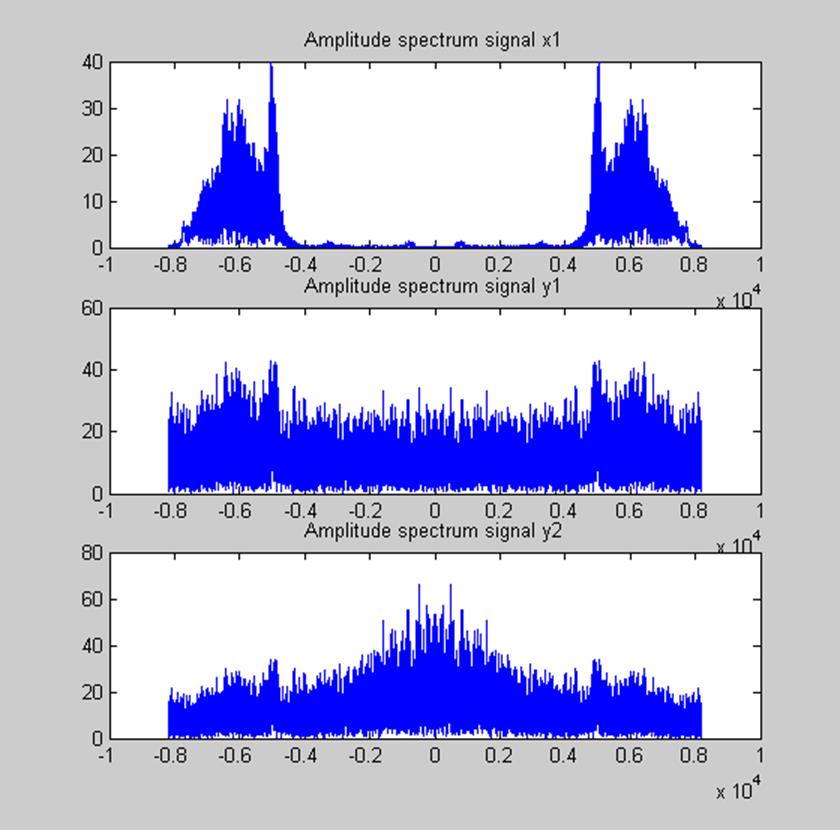
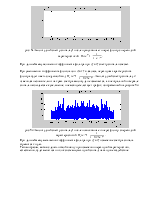
рис. 8 Амплитудный
спектр исходного сигнала, амплитудный спектр исходного сигнала с наложением на
него шумов, амплитудный спектр сигнала у1 после пропускания его через фильтр с
переходной характеристикой 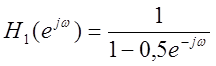 .
.
При прослушивании сигнала х1 и у1 очень сильно заметны различия в звучании. Все объясняется тем, что на сигнал х1 накладываются посторонние шумы, и это видно из графика амплитудных спектров сигналов х1 и у1. После пропускания сигнала у1 через фильтр с переходной функцией
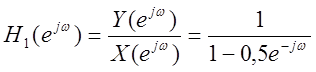 заметно понижается
громкость сигнала в начале и в конце сигнала, но в середине звучания громкость
сигнала усиливается, что подтверждается графиками амплитудных спектров сигналов
у1 и у2.
заметно понижается
громкость сигнала в начале и в конце сигнала, но в середине звучания громкость
сигнала усиливается, что подтверждается графиками амплитудных спектров сигналов
у1 и у2.
При увеличении коэффициента фильтра при y[n-1] в два раза, переходная
характеристика фильтра будет иметь следующий вид: 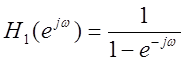 .
Амплитудный спектр сигнала у2 изменился: на краях спектра амплитуда стремится к
нулю, а в центральной точке сигнала наблюдается её резкое увеличение, о чем
свидетельствует график, изображенный на рисунке 8а.
.
Амплитудный спектр сигнала у2 изменился: на краях спектра амплитуда стремится к
нулю, а в центральной точке сигнала наблюдается её резкое увеличение, о чем
свидетельствует график, изображенный на рисунке 8а.
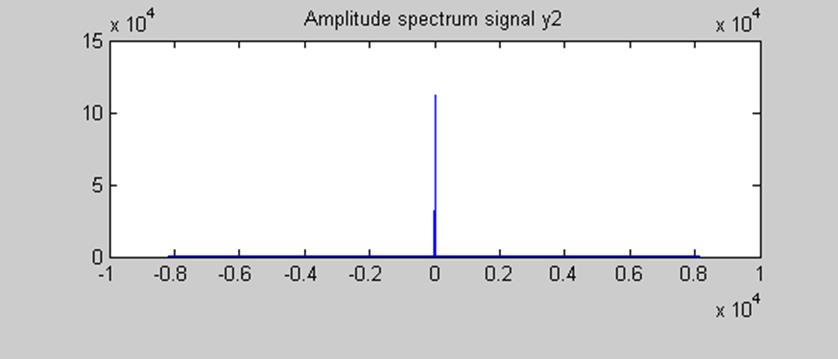
рис. 8а Амплитудный
спектр сигнала у1 после пропускания его через фильтр с переходной
характеристикой 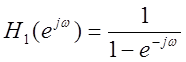 .
.
При дальнейшем увеличении коэффициента фильтра при y[n-1] спектр сигнала исчезает.
При уменьшении коэффициента фильтра при y[n-1] в два раза,
переходная характеристика фильтра будет иметь следующий вид: 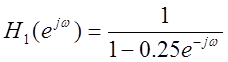 . Амплитудный спектр сигнала у2
изменился незначительно: на краях спектра амплитуда не изменяется, а в центральной
интервале сигнала наблюдается её увеличение, о чем свидетельствует график,
изображенный на рисунке 8б.
. Амплитудный спектр сигнала у2
изменился незначительно: на краях спектра амплитуда не изменяется, а в центральной
интервале сигнала наблюдается её увеличение, о чем свидетельствует график,
изображенный на рисунке 8б.
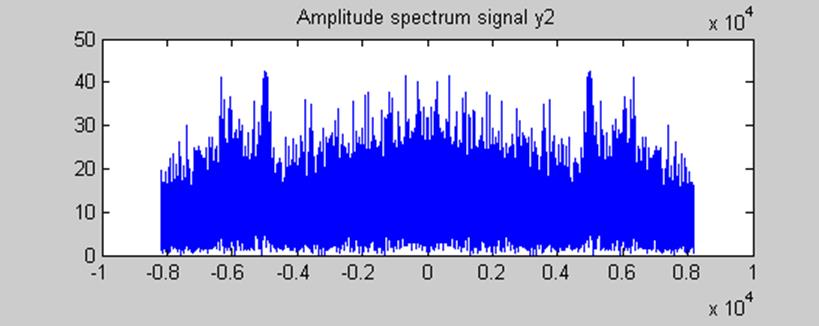
рис. 8б Амплитудный
спектр сигнала у1 после пропускания его через фильтр с переходной
характеристикой 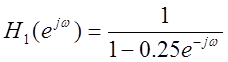 .
.
При дальнейшем уменьшении коэффициента фильтра при y[n-1] изменение спектра сигнала стремится к нулю.
Таким образом, можно сделать общий вывод: при изменении переходной характеристики, естественно, будет меняться и оклик системы (выходной сигнал) на входное воздействие.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.