







Оглавление
Задача 4. 3
Задача 14. 3
Задача 24. 4
Задача 34. 4
Задача 44. 6
Задача 54. 8
Список литературы.. 9
Решение:
Запишем уравнение плоскости p в параметрическом виде:
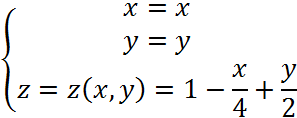
Найдем частные производные:
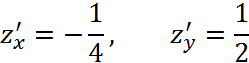
Пусть, множество ![]()
Тогда, поверхностный интеграл можно выразить через двойной:

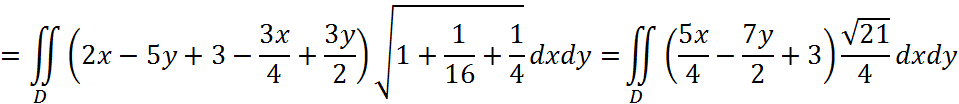
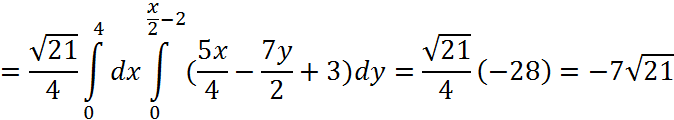
Решение:
Запишем компоненты векторного
поля ![]() :
:
![]()
Уравнение сферы в сферических координатах:
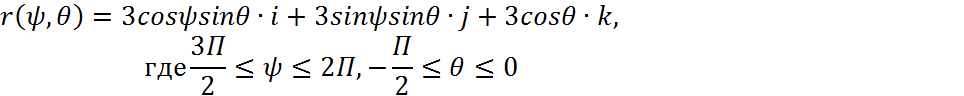
Применим формулу Стокса:
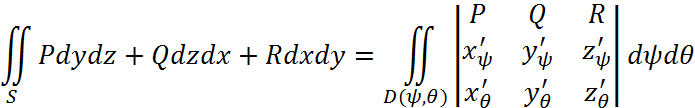
Т.к.
![]()
![]()
Тогда:
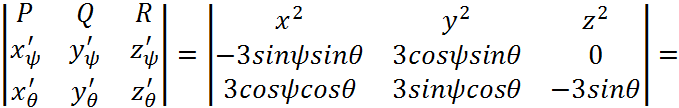
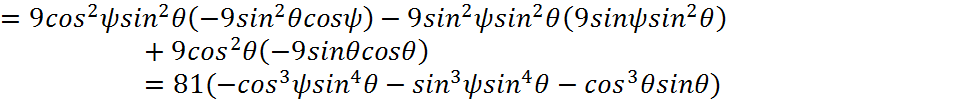
Это значение соответствует внутренней нормали.
Тогда, искомый интеграл:
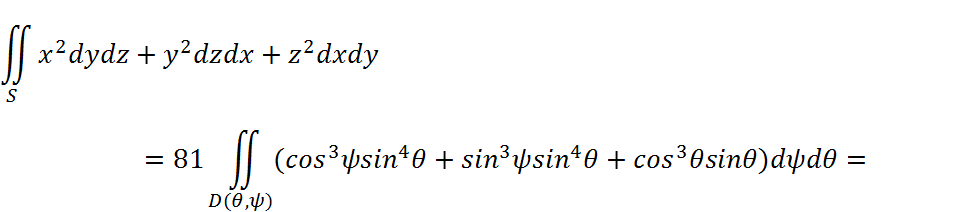
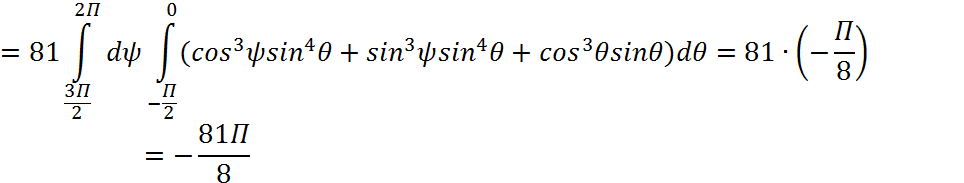
Решение:
1)
![]()
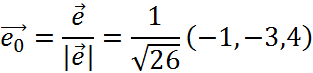
Тогда, производная функции по
направлению ![]() :
:
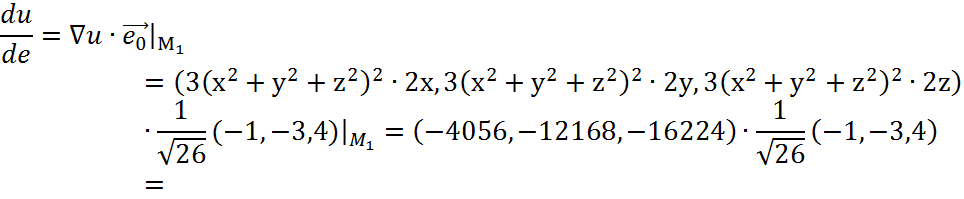
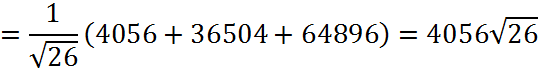
2)
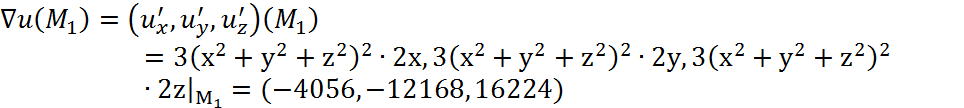
Решение:
1)
Искомый поток векторного поля
![]() через поверхность
через поверхность ![]() – это интеграл:
– это интеграл:
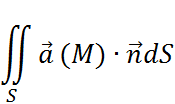
Где ![]() - единичный вектор внешней нормали.
- единичный вектор внешней нормали.
S – поверхность пирамиды:
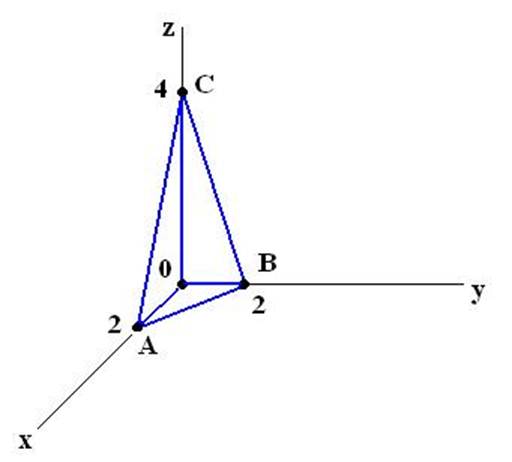
Т.к. поверхность S состоит из 4 гладких «кусочков», то запишем этот интеграл в виде суммы:
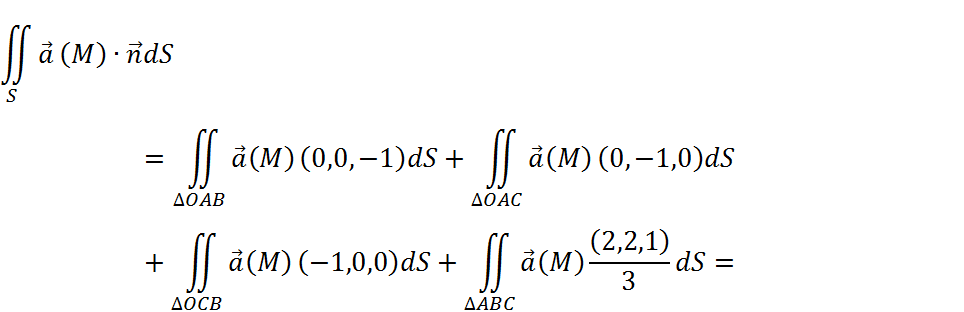
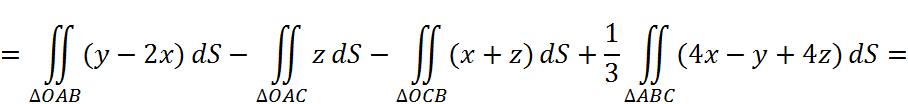
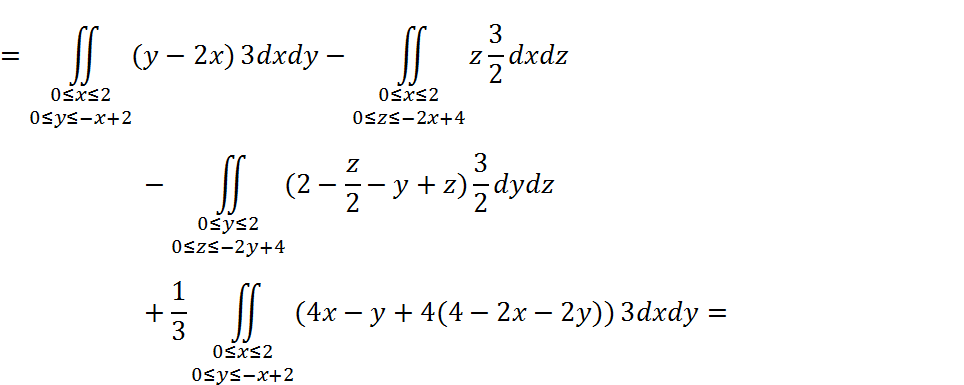
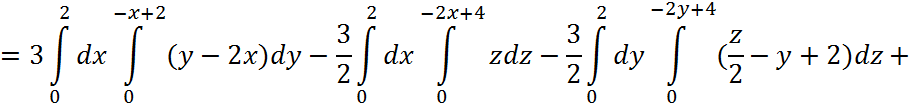
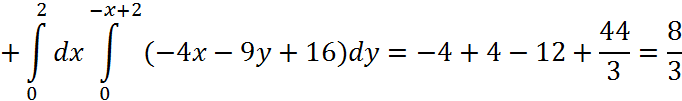
2)
Посчитаем исходный интеграл с помощью формулы Остроградского-Гаусса:

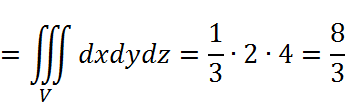
Решение:
1)
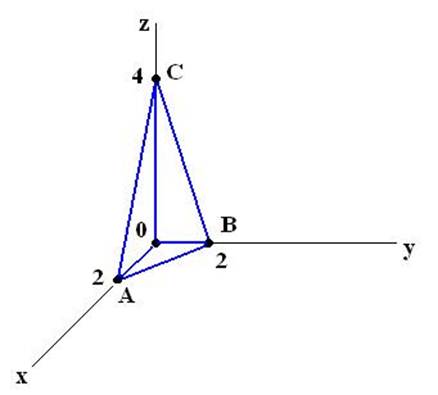
Циркуляция векторного поля ![]() по контуру C треугольника с вершинами в
токах (2,0,0), (0,2,0), (0,0,4) – это интеграл:
по контуру C треугольника с вершинами в
токах (2,0,0), (0,2,0), (0,0,4) – это интеграл:
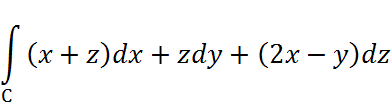
Посчитаем интеграл на каждой стороне треугольника:
Сторона АВ задается параметрически:
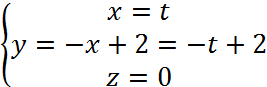
Тогда интеграл по стоне АВ:
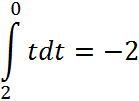
Сторона ВС задается параметрически:
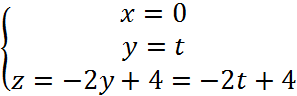
Тогда интеграл по стороне ВC:
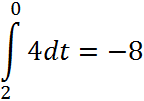
Сторона CA задается параметрически:
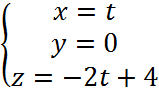
Тогда интеграл по стоне АВ:
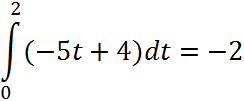
Тогда исходный интеграл:
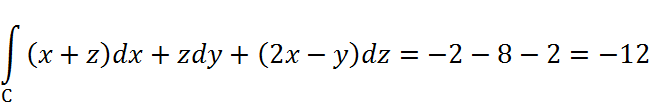
2)
Посчитаем интеграл с помощью формулы Стокса.
Пусть S –
это поверхность, ограниченная треугольником ABC, а ![]() – нормаль к ней. Тогда:
– нормаль к ней. Тогда:
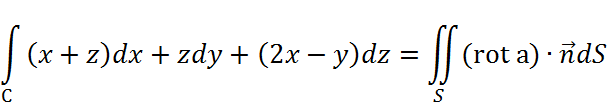
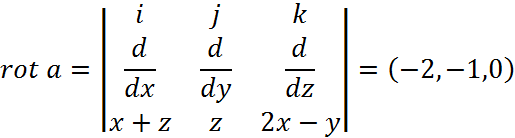
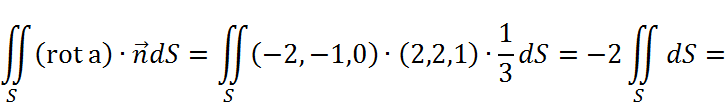
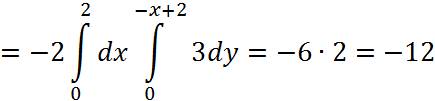
Решение:
Запишем компоненты векторного
поля ![]() :
:
![]()
Для того, чтобы поле было потенциальным, необходимо:
![]()
Проверим это условие:
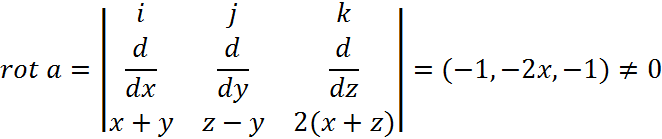
Т.е. векторное поле ![]()
Берс Л. Математический анализ. M.: Высш. шк., 1975. Т. 1–2.
Зорич В. А. Математический анализ. М.: Наука, 1981. Т. 1–2.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчис-ления. М.: Наука, 1969. Т. 1–3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.