Система слежения за направлением. Анализ, выбор и расчет основных параметров типовых радиотехнических следящих систем, страница 3

Физический смысл существования оптимального значения полосы объясняется следующим. При малых значениях F_m основной вклад в результирующую ошибку вносит составляющая е_а, а при больших F_m -шумовая составляющая е_п, поэтому соответствует оптимальное значение шумовой полосы F_mom при котором результирующая ошибка минимальна.

Графики зависимостей результирующей средней квадратической ошибки слежения, а также ее составляющих (динамической и шумовой) от коэффициента передачи интегратора и полосы показаны на рис. 2.2.

X

\

\

V

Лисп

160200 ДФ 210302.65 К24 ПЗ

Лист

№докум

Аазочастотнпй     tiUbW'"*...... ~~"^А  ™^11ЛИТУД^н°-^частотной (ЛАХ) и

фазочастотнои (ЛФХ) характеристик разомкнутой системы и определение по „им запаса устойчивости по амплитуде и фазе при оптимальном значении параметра к_и.

Передаточная функция разомкнутой системы К (п)-  ^д " (      ^lP'

^р     р о+ад

7;= 0,06 с,  Г₂= 5,6 с, /с_л= 1,5 В/град, к_иот = 21,9. со_с1=\6,1 с"¹ , а)_с2=0,2 с"',

ЛАХ:

Ч \

• XX

ЛФХ: (р{а>) =------ + arctg{Q)T,) - arctg{Q)T₂).

,ДБ

-100

0.01            0.1

,1/с

V

№докум

Рис. 3.1-ЛАХ, ЛФХ

160200 ДФ 210302.65 К24Ш

Лисп

3  Построение логарифмических амплитудно-частотной ГЛА*>
фазочастотнои     (ЛФХ)     характеристик     разомкнутой     с„сте_М^ „
определение  по  „им  запаса  устойчивости  „о амплитуде и Тазе „₀„
оптимальном значении параметра к_и.                                        ^{Ф         Р}

\\\

Передаточная функция разомкнутой системы- К (n)-^kjlku (¹

"     р о+ад

7;= 0,06 с, Г₂= 5,6 с, Л_д= 1,5 В/град, А^ = 21,9. <Ч, =16,7 с"¹ , ю_г2=0,2 с⁴,

ЛАХ:

ЛФХ: ^(<У) =----- + arctg(Q)T_x) - arctg(u)T₂).

X        г

1/с

X

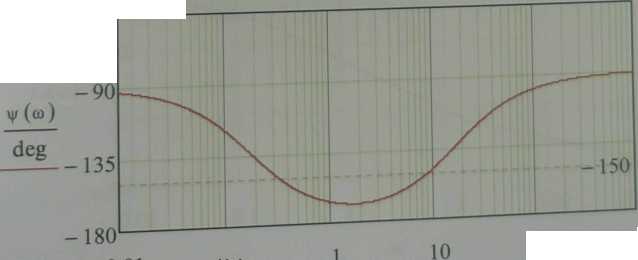, град

0.1

 Л/с

Рис. 3.1-ЛАХ, ЛФХ

VI

I

Рис. 3.2 - К определению запаса устойчивости

Значение шумовой полосы ^ =5,18 Гц. Результирующая ошибка слежения е-0.2- град.

р     ^иян;г_иГ1-       ~

дальше расположена АФХ от к™™^    -     ^{уСТОИЧИВОС}™ ™ больше, чем

я-|Л»,)|. частота при которой £(„) = (, - _частота среза разомкнув системы а,,. В нашем случае ЛФХ не достигает значен™ _йр =_,, _{запас п0} амплитуде выполняется всегда, не требует оценки.

 = я-|?Н<Ч_р)|=180-167 =

—,   запас   устойчивости   по   фазе   не

достаточный.

По графику видно, для требуемого запаса устойчивости по фазе —,

6

необходимо либо увеличить 0)^ до 10 с"¹, либо уменьшить до 0,3 с"'. Оба эти значения трудно реализовать путем только лишь изменения к_и. Для оптимального результата желательно также уменьшить постоянную времени Т₂ и увеличить Т_х.

Реализовать 0)^ —10 более предпочтительнее, чем «^=0,3 с"¹. Для реализации О) =0,3 с"¹ нам потребуется уменьшить к_и как минимум до единичного значения, при котором результирующая ошибка очень высока

(рис. 2.2).

Поэтому    увеличим        к_и    до    300,    обеспечив   требуемый   запас

устойчивости. Проведем пересчет.

к_и - 300,    СО   = 10 с"¹, запас устойчивости выполняется.

г а

\