Используя для описания помехи модель белого шума, дисперсия шумовой ошибки определяется:
# ш'
где F - так называемая шумовая полоса замкнутой системы.
При заданной спектральной плотности No определение дисперсии шумовой ошибки сводится к вычислению шумовой полосы системы. Для типовых систем радиоавтоматики определенный интеграл сводится к
|
табличному интегралу /„=— J Вп{со) определяются как: |
|
|
|
Квадрат АЧХ замкнутой системы: \К |
|
|
где полиномы An(jco) и
\ ■
\е.
Лист
160200ДФ 210302.65К24Ю
![]() |Изм \Лист\ л/°
|Изм \Лист\ л/°
Подпись
Дал
V
ч\\
V
![]()
![]() 2 Оптимизация следящей системы по
параметру к , используя критерий максимума среднего квадрата ошибки; определение оптимального
значения шумовой полосы /ш системы и минимально достижимой ошибки
слежения стт; построение графиков зависимостей результирующей
средней квадратической ошибки слежения, а также ее составляющих
(динамической и шумовой) от полосы.
2 Оптимизация следящей системы по
параметру к , используя критерий максимума среднего квадрата ошибки; определение оптимального
значения шумовой полосы /ш системы и минимально достижимой ошибки
слежения стт; построение графиков зависимостей результирующей
средней квадратической ошибки слежения, а также ее составляющих
(динамической и шумовой) от полосы.
В зависимости от характера воздействия x(t) (детерминированное или случайное) точность следящих систем в условиях действия помех оценивается либо средним квадратом либо дисперсией, в нашем случае средним квадратом ~ё2 = е\ + а2п. Значение динамической ошибки ел
определяет математическое ожидание (среднее значение) ошибки слежения при детерминированном воздействии.
Используя для описания помехи модель белого шума, дисперсия шумовой ошибки определяется:
![]()
![]()
![]() д0 где Fm
-
так называемая шумовая полоса замкнутой системы.
д0 где Fm
-
так называемая шумовая полоса замкнутой системы.
|
где полиномы An{jiui |
При заданной спектральной плотности Мо определение дисперсии шумовой ошибки сводится к вычислению шумовой полосы системы. Для типовых систем радиоавтоматики определенный интеграл сводится к
табличному интегралу /„ = — В {со) определяются как:
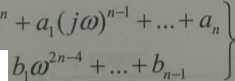
Вп(со) = Ь0со-п- +
Квадрат АЧХ замкнутой системы:
2 = К,(со) =
_т
к к (x-
|
В„(О)) _
|
|
/ --__
|
2aoa, |
2 ^
![]() 2 "
2 "
2 _
![]() В итоге средний квадрат результирующей
ошибки:
В итоге средний квадрат результирующей
ошибки:
+ ■
2x10 |
|
1x10 |
|
-4 |
|
-1x10 |
|
400 |
 Математическая формулировка задачи
параметрической оптимизации сводится к нахождению экстремума (минимума)
функции, в данном случае, одной
переменной ки.
Математическая формулировка задачи
параметрической оптимизации сводится к нахождению экстремума (минимума)
функции, в данном случае, одной
переменной ки.
50 ЮО 150 200 250 300
\
X
\
V
|
0.075 |
|
0.05 |
|
0.025 |
 О 50
О 50
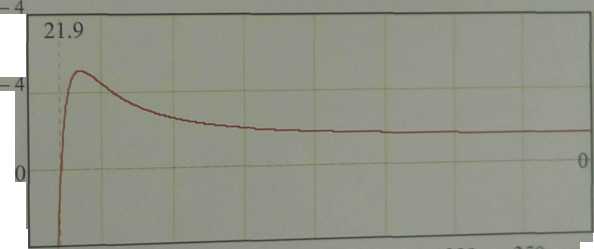
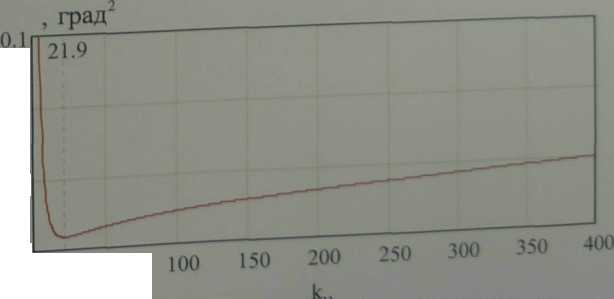
Рис. 2.1 - Производная функции ё\Ю по k., функция
![]()
\ ъ % Ъ
2
![]() В итоге средний
квадрат результирующей ошибки:
В итоге средний
квадрат результирующей ошибки:
^ _ 2 , _2 _
+ ■
![]() Математическая
формулировка задачи параметрической оптимизации сводится к нахождению
экстремума (минимума) функции, в данном случае, одной переменной ки.
Математическая
формулировка задачи параметрической оптимизации сводится к нахождению
экстремума (минимума) функции, в данном случае, одной переменной ки.
2x10
-4
21.9
1x10
-4
|
|
|
О 50 100 |
|
0 50 |
 -1x10
-1x10
-4
150 200 250 300 350 400 к.,
---------------------------- ^7« ini\ 150 400
,00 150 200 ?<0 300 350
|
|
|
,2.1 Производная функции, ,U по/ Фуикиия Г |
|
(*.) |
|
160200 ДФ 210302.65 К24Ю |
 \\\
\\\
![]() Как видно из рис 2 1 к
Как видно из рис 2 1 к
минимум,
либо производная 2"' "^ К°Т°Р°Й
ФуНКЦИЯ ^{к"> имеет
А_
= 21,9.Д ФУНКЦИИ
пР°х°Дит через нуль, имеет значение
Оптимальное значение пп/м
ошибку находим подстановкой^ П°Л°СЫ И минимально Достижимую
д iciHOBKon kuom в соответствующие выражения
F
\
![]()
![]()
![]() \kuom)=0M град.
\kuom)=0M град.
Физический смысл существования оптимального значения полосы объясняется следующим. При малых значениях F[U основной вклад в
результирующую ошибку вносит составляющая е2, а при больших Fm -шумовая составляющая еп, поэтому соответствует оптимальное значение шумовой полосы FlU0in при котором результирующая ошибка минимальна.
Графики зависимостей результирующей средней квадратической ошибки слежения, а также ее составляющих (динамической и шумовой) от коэффициента передачи интегратора и полосы показаны на рис. 2.2.
\
X
\
ч N

\
|
|
Как видно из рис. 2 1 k
минимум,
либо производная Zu "^ К°Т°Р°Й
Функция *\k) имеет
*.«л =
21,9. ФУНКЦИИ проходит через нуль, имеет значение
Оптимальное значение щ
|
+ Т2кк ___ *■ п и опт |
ошибку находим подстановкой JM°B°H
полосы и минимально
достижимую
2 "™
в со°тветствующие выражения.
|
к Т) д иопт 1 ) |
шопт
\
Ь \ Ь.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.