Пример 3.1. Синтез передаточной функции рекурсивного фильтра по аналоговому прототипу. В соответствии с методом билинейного преобразования синтезирован рекурсивный полосно-пропускающий фильтр, заданный параметрами своей частотной характеристики. Синтез выполнен с помощью программы РЦФ-СИНТЕЗ, разработанной студентами Захарченко М. О., Ставер В. В. под руководством автора. Ниже приводятся данные и графики, выводимые программой, которая автоматически ведет протокол расчетов, начиная с ввода пользователем исходных данных. Для сопоставления рассчитаны необходимые порядки АФПНЧ для аппроксимирующих функций Баттерворта (m =15), Чебышева (прямой и инверсной, m = 7) и Золотарева – Кауэра (m = 5). В качестве прототипа цифрового фильтра принят аналоговый фильтр Золотарева – Кауэра, называемый также эллиптическим.
Тип фильтра - Полосовой
-------------- Граничные частоты ЦФ -----------------
Первая частота среза Fc1 = 8400
Вторая частота среза Fc2 = 11600
Первая частота задерживания Fз1 = 7600
Вторая частота задерживания Fз1 = 12400
-------------- Требования к АЧХ ЦФ ------------------
Неравномерность в полосе пропускания Ап = 1.000
Затухание в полосе задерживания Аз = 40.000
Частота дискретизации Fд = 112000
-------------- Граничные частоты АФПНЧ -----------------
Нормированная частота среза АФПНЧ = 1.0000000
Нормированная частота задерживания АФПНЧ = 1.4303418
------------------ Синтез АФПНЧ ---------------------
Аппроксимация Баттерворта (по Тейлору)
Порядок АФПНЧ = 15
Аппроксимация Чебышева прямая
Порядок АФПНЧ = 7
Аппроксимация Чебышева инверсная
Порядок АФПНЧ = 7
Аппроксимация Золотарева-Кауэра (эллиптическая)
Порядок АФПНЧ = 5
---- Полюса АФПНЧ ---- --- Нули АФПНЧ ----
(для аппроксимации Золотарева-Кауэра)
Pp[1]=-0.227645373 + (-0.691258748)*j P0[1]=0.000000000 + (-2.197510941)*j
Pp[2]=-0.227645373 + (0.691258748)*j P0[2]=0.000000000 + (2.197510941)*j
Pp[3]=-0.063690094 + (-0.995808482)*j P0[3]=0.000000000 + (-1.482755953)*j
Pp[4]=-0.063690094 + (0.995808482)*j P0[4]=0.000000000 + (1.482755953)*j
Pp[5]=-0.345050270 + (0.000000000)*j P0[5]= бесконечен
----------- Результаты билинейного преобразования ----------
Порядок ЦФ = 10
Нормирующий множитель фильтра С = 0.001484825408
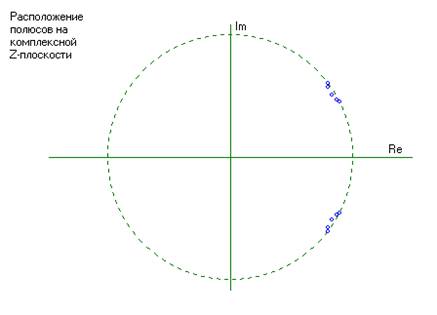
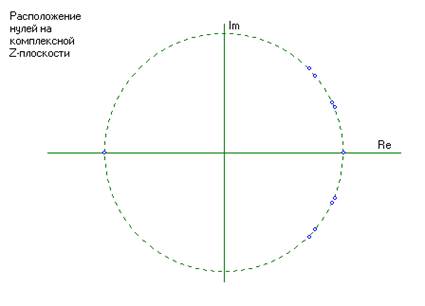
---- Полюса ЦФ ---- ----Нули ЦФ ----
Zp[1]=0.863876936 + (0.466514453)*j Z0[1]=0.925200000 + (0.379479855)*j
Zp[2]=0.863876936 + (-0.466514453)*j Z0[2]=0.925200000 + (-0.379479855)*j
Zp[3]=0.796109586 + (-0.567716076)*j Z0[3]=0.711087038 + (0.703103992)*j
Zp[4]=0.796109586 + (0.567716076)*j Z0[4]=0.711087038 + (-0.703103992)*j
Zp[5]=0.790741976 + (-0.601510989)*j Z0[5]=0.906492380 + (0.422222176)*j
Zp[6]=0.790741976 + (0.601510989)*j Z0[6]=0.906492380 + (-0.422222176)*j
Zp[7]=0.886540728 + (0.452042343)*j Z0[7]=0.764050169 + (0.645156833)*j
Zp[8]=0.886540728 + (-0.452042343)*j Z0[8]=0.764050169 + (-0.645156833)*j
Zp[9]=0.824540464 + (0.509797598)*j Z0[9]=1.000000000 + (0.000000000)*j
Zp[10]=0.824540464 + (-0.509797598)*j Z0[10]=-1.000000000 + (0.000000000)*j
 Коэффициенты
РЦФ каскадной формы реализации
Коэффициенты
РЦФ каскадной формы реализации
Количество звеньев = 5
-------------------------------------------
b0[1]= 1 b1[1]= -1.8504 b2[1]= 1 a1[1]= -1.72775387 a2[1]= 0.963919096
b0[2]= 1 b1[2]= -1.42217408 b2[2]= 1 a1[2]= -1.59221917 a2[2]= 0.956092015
b0[3]= 1 b1[3]= -1.81298476 b2[3]= 1 a1[3]= -1.58148395 a2[3]= 0.987088342
b0[4]= 1 b1[4]= -1.52810034 b2[4]= 1 a1[4]= -1.77308146 a2[4]= 0.990296742
b0[5]= 1 b1[5]= 0 b2[5]=-1 a1[5]= -1.64908093 a2[5]= 0.939760568
Коэффициенты РЦФ параллельной формы реализации
Количество звеньев = 5
----------------------------------------------
b0[1]=-25.009829 b1[1]=24.160216 b2[1]= 0 a1[1]=-1.7277538 a2[1]= 0.96391909
b0[2]=-17.752916 b1[2]=28.668925 b2[2]= 0 a1[2]=-1.5922191 a2[2]= 0.95609201
b0[3]= 1.6675599 b1[3]=-6.678022 b2[3]= 0 a1[3]=-1.5814839 a2[3]= 0.98708834
b0[4]= 6.6073541 b1[4]=-5.108268 b2[4]= 0 a1[4]=-1.7730814 a2[4]= 0.99029674
b0[5]= 36.197792 b1[5]=-42.57829 b2[5]= 0 a1[5]=-1.6490809 a2[5]= 0.93976056
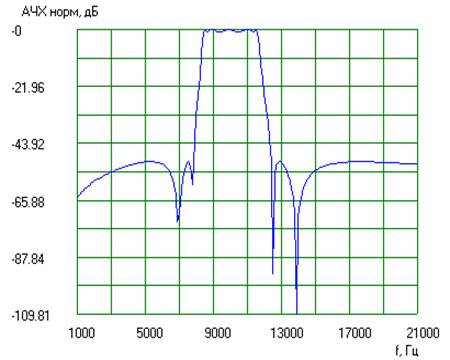
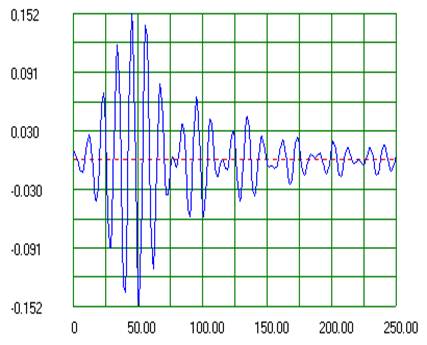
В соответствии с рассмотренными методами для синтезируемого в главе 3 (пример 3.1) рекурсивного цифрового фильтра рассчитаны масштабные множители, выходные шумы квантования АЦП и произведений, получены отклики фильтра на гармонические сигналы, вычислены статистические оценки шума квантования на входе и выходе фильтра. Расчеты и моделирование выполнены с помощью программы РЦФ-СИНТЕЗ. Ниже приводятся протокол расчетов и графики, выводимые программой, а также соответствующие используемой методике промежуточные данные этих расчетов.
---------------Параметры структуры ЦФ ----------------
Форма реализации фильтра - каскадная
Форма реализации звеньев - каноническая
Способ ограничения разрядности - округление
Ограничение разрядности коэффициентов = 15 бит
Ограничение разрядности произведений – путем округления сумм произведений.
--------- Данные для расчета масштабных множителей --------
Сумма модулей ИХ всего фильтра S|h(n)| = 1836,78
Сумма квадратов ИХ всего фильтра Sh2(n) = 23924,72
Максимум АЧХ всего фильтра |H(jf)|max = 672,60
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.