Выбор частоты среза производится с учетом противоречивых требований: подавления сигнала опорной частоты, малой дисперсии фазового шума на выходе и приемлемого времени перестройки. Увеличение fСР с целью повышения быстродействия системы влечет увеличение уровня ПСС на выходе синтезатора, обусловленных прохождением опорного сигнала (степень его подавления определяется значением ЛАХ L(2πf0), см. рис. 22). Влияние остаточного фона с амплитудой Uит0 и частотой f0 (высшими гармониками опорного сигнала можно пренебречь) приводит к частотной модуляции выходного сигнала ПГ с индексом
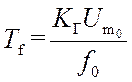
Например, при f0 = 1 кГц, Кг =50 кГц/В и приемлемом значении mf ≤ 10-3 (побочные спектральные составляющие имеют уровень -60 дБ) получаем, что амплитуда остаточного фона опорного сигнала не должна превышать 20 мкВ. При высоких требованиях к уровню ПСС для ослабления паразитной модуляции в цепи
управления частотой ПГ устанавливают режекторные фильтры, подавляющие остаточный фон опорного сигнала, например, двойной Т – образной RС – мост.
Рассмотрим теперь влияние частоты среза на уровень фазовых флуктуаций выходного сигнала синтезатора. Система ФАПЧ является своеобразным частотным фильтром по отношению к шумам, действующим в системе. Поскольку фазовый шум δφ0(t) воздействует на вход системы, а фазовый шум δφг(t) - на ее выход (см. рис.21), то и фильтрация их осуществляется по-разному (коэффициенты передачи, а следовательно, и АЧХ системы различны по отношению к ним).
Дисперсии составляющих фазового шума на выходе системы, обусловленных воздействием шумов δφ0(t) и δφг(t), равны соответственно
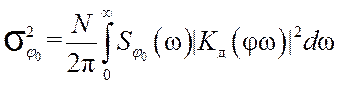(21)
и
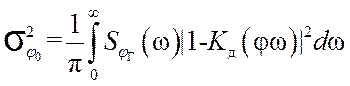, (22)
где Sφ0(ω) и Sφг(ω) - соответственно спектральная плотность фазового
шума формирователя опорного сигнала и ПГ; спектральная плотность Sφ0(ω) связана со спектральной плотностью фазового шума
КГ соотношением Sφ0(ω)= Sφ0(ω)/М2 ( М –коэффициент
деления частоты в тракте формирования опорного сигнала); 
– комплексный коэффициент передачи
замкнутой системы по входу δφ0 ; 
–
комплексный коэффициент передачи замкнутой системы по входу δφг.
Графики, представленные на рис.23, поясняют механизм фильтрации фазовых шумов в
системе ФАПЧ. Низкочастотный фазовый шум КГ с "весом", равным 
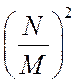, переносится на выход системы, а
высокочастотные его составляющие подавляются (кольцо ФАПЧ эквивалентно фильтру
нижних частот). Иначе ведет себя система по отношению к фазовому шуму ПГ;
низкочастотные спектральные составляющие она подавляет, а высокочастотные
воспроизводит (т.е. является фильтром верхних частот). Существует оптимальное
значение шумовой полосы Fш системы,
при которой дисперсия результирующего фазового шума минимальна.
σφ2 = σ φ02 + σ φг2 (23)
Для оптимизации систем по этому критерию необходимо знать спектральные характеристики Sφк(ω) и Sφг(ω) фазовых шумов. В большинстве случаев допустимо полагать фазовый шум КГ белым (по крайней мере в полосе системы Fш ) со спектральной плотностью Sφк(f)=Nφ0, рад2/Гц. При этом дисперсия фазового шума (21), рад2
σ φ02 = N2Nφ0Fш/M2.
Шумовая полоса системы
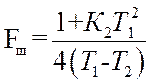
при оптимальном выборе параметров ФНЧ в соответствии с (20) равна 6πfСР/8.
Спектральная плотность фазовых флуктуаций ПГ допускает аппроксимацию в виде
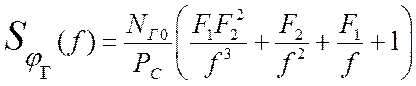, (24)
где РС -мощность колебания на входе ПГ; NГ0=КшkT- спектральная плотность шума на входе ПГ (Кш – коэффициент шума активного элемента ПГ; К = 1,38 • 10-23 Дж/К - постоянная Больцмана; Т – температура, град∙К; F1 – частота, при которой уровень фликкер-шума (составляющая фазового шума на входе ПГ со спектром вида 1/f) равен уровню белого шума; F2=fГ0/2Q – половила полосы пропускания резонансного контура ПГ (Q – добротность контура, fГ0 – частота ПГ).
Использование модели спектра (24) для нахождения дисперсии фазового шума в соответствии с формулой (22) затруднительно. Для практических расчетов используют асимптотические логарифмические спектральные характеристики (рис. 24). При этом ось частоты разбивают на декады, а частоты F1 и F2 имеют, смысл частот сопряжения асимптот с наклоном соответственно -30 и -20 (дБ/дек) и -20 и 0 (дБ/дек).
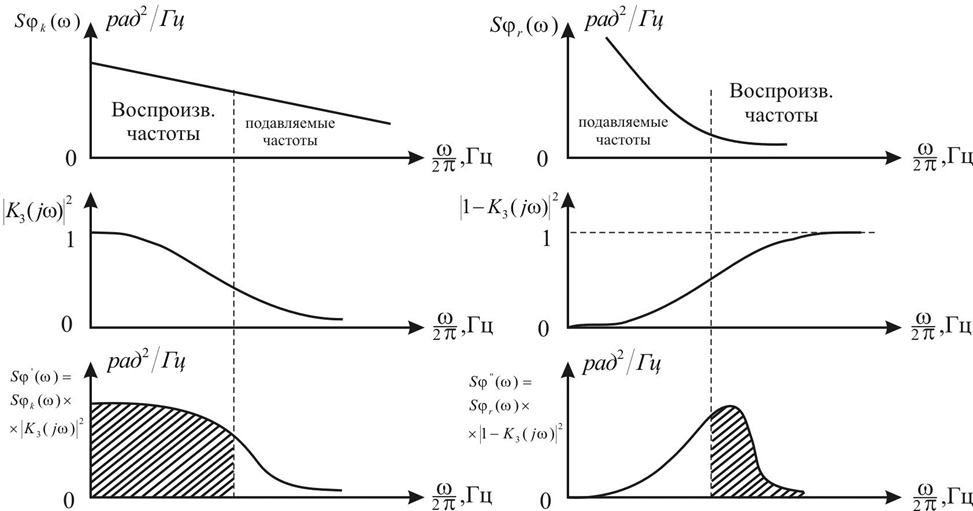
Рис. 23. Энергетические спектры фазовых шумов и частотные
характеристики системы
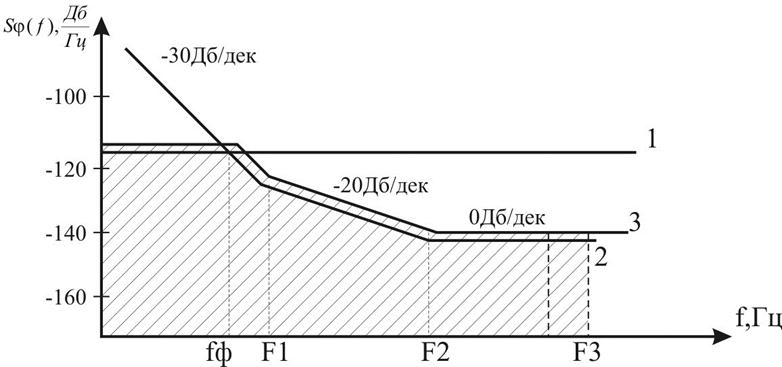
Рис. 24. Логарифмические спектральные характеристики
фазовых шумов: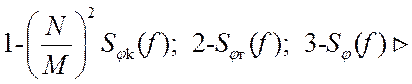 
Оптимизация полосы системы сводится к выбору такого значения fCР , которое соответствует равенству спектральных характеристик КГ и ПГ, приближенно это эквивалентно оптимизации по критерию (6). Физическое обоснование такого выбора следующее. При fСР<fСР.ОПТ основной вклад в результирующий фазовый шум вносит ПГ, а при обратном соотношении кварцевый генератор, так что минимум дисперсии фазового шума на выходе ПГ достигается при приблизительном равенстве уровней фазовых шумов обоих генераторов.
На практике в качестве показателя спектральной чистоты выходного сигнала синтезатора в соответствии с требованиями ГОСТ используют дисперсию фазового шума в полосе частот от 0 до FВ (численно равную площади заштрихованной фигуры на рис. 24) и выраженную в дБ. Например, уровень фазового шума -100 дБ означает, что дисперсия в полосе FВ (обычно кратной 10 Гц) составляет 10-10 рад2. При этом задается еще требуемый уровень побочных спектральных составляющих (выраженный в дБ относительно амплитуды гармонического сигнала частоты fч0).
4. Домашнее задание
1. Нарисовать функциональную схему синтезатора частот.
2. Изобразить функциональную схему и дискриминационные характеристики ИЧФД (фазовую и частотную).
3. Произвести выбор параметров ФНЧ, полагая напряжение источника питания Е = 5 В, сопротивление открытого ключа RКЛ = 1,6 кОм, крутизну регулировочной характеристики ПГ Кг = 50 кГц/В, коэффициент деления ДПКД N=1000 (значение частоты среза взять из табл. 3).
Таблица 3
Значение fСР/f0
|
№бригады №группы |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
0,05 |
0,08 |
0,01 |
0,04 |
0,07 |
0,09 |
|
2 |
0,03 |
0,06 |
0,09 |
0,02 |
0,05 |
0,08 |
|
3 |
0,02 |
0,04 |
0,07 |
0,1 |
0,03 |
0,06 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.