Радиоавтоматика: Учебное пособие по лабораторному практикуму, страница 10

●    ознакомиться  с методическими указаниями к работе и изучить соответствующие разделы рекомендованной литературы;

●    ознакомится с функциональной схемой лабораторного макета системы ФАПЧ и изучить принцип его работы.

2. Краткие теоретические сведения

Системы ФАПЧ находят широкое применение в современных ра­диотехнических системах: для стабилизации промежуточной часто­ты приемников, в качестве следящих фильтров доплеровских изме­рителей скорости, следящих измерителей координат подвижных объектов, демодуляторов сигналов с частотной и фазовой моду­ляцией, в синтезаторах частот.

В общем случае функциональная схема системы ФАПЧ (рис. 10) включает фазовый дискримина­тор (ФД), фильтр нижних час­тот (ФНЧ) и подстраиваемый генератор (ПГ).

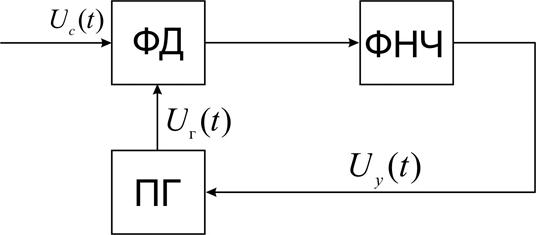
Рис. 10. Функциональная схема системы ФАПЧ

На входы ФД поступают сигнал   и опорное колебание , выраба­тываемое подстраиваемым генератором. Если частоты колебаний сигнала и ПГ совпадают (начальная частотная расстройка ), то в стационарном режиме напряжение на выходе ФД равно нулю, а фазовый сдвиг 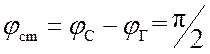. Обычно начальная расстройка   (вследствие неста­бильности частоты ПГ, доплеровского сдвига частоты сигнала). В этом случае на выходе ФД возникают биения с частотой . Это напряжение воздействует на управляющий элемент ПГ (например, варикап), осуществляя частотную модуляцию колебания . В зависимости от знака управляющего напряжения  частота биений то возрастает, то убывает. В резуль­тате длительности положительных и отрицательных полуволн напряжения биений различны и на выходе ФД образуется постоян­ная составляющая напряжения, которая уменьшает частоту биений относительно начальной расстройки . ФНЧ пропускает постоянное напряжение, но отфильтровывает мешающие составляю­щие, которые, попадая на управляющий элемент ПГ, вызывали бы паразитную частотную модуляцию колебания  .

Если начальная расстройка не превышает значения , определяющего полосу захвата, то в системе устанавливается стационарный режим (режим слежения), при котором  (), а фазовый сдвиг колебаний сигнала и ПГ – 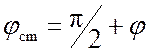 , где  – фазовая ошибка (обычно ). При этом на выходе ФД устанавливается постоянное напряжение, компенсирующее частотную расстройку  . Если начальная частотная расстройка  , то напряжения, подавае­мого на управляющий элемент ПГ, недостаточно для ее компен­сации и стационарный режим невозможен. Этот режим (режим биений) характеризуется тем, что среднее значение частоте  отличается от частоты , а разность фаз непрерывно на­растает.

Для того чтобы вывести систему из стационарного режима, необходимо изменить частоту сигнала относительно номинального значения на величину  , определяющую полосу удержания системы (область частотных расстроек, в которой возможен ре­жим слежения).

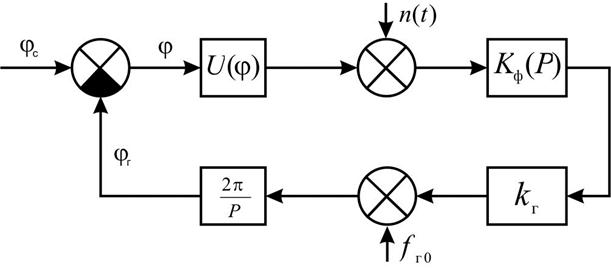
Рис. 11. Структурная схема системы ФАПЧ

Анализ качественных показателей системы ФАПЧ (запас устой­чивости, быстродействие, точность, полосы захвата и удержания) проводят на основе структурной схемы (рис.11), под которой понимают математичес­кую модель системы, представленную в виде набора определённых звеньев, реализующих заданные математичес­кие операции.

Полагая, что шум  отсутствует, запишем дифференциальное уравнение системы ФАПЧ в операторной форме

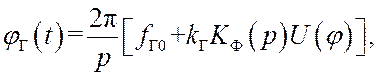                          (11)

где  – оператор интегрирования;  – собственная частота ПГ (при разомкнутой обратной связи);  – крутизна регулировочной характеристики ПГ в Гц/В;  – передаточ­ная функция ФНЧ;  – дискриминационная характеристика ФД.

Уравнение (11) можно представить в виде

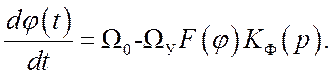                                      (12)

Здесь     – начальная расстройка в рад/с; 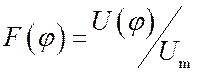 – нормированная дискриминационная характеристика ( – максимальное значение напряжения на выходе ФД);  ( – полоса удержания в рад/с).

Обычно дискриминационная характеристика  (нулевой фазовой ошибке соответствует постоянный фазовый сдвиг  сигнала и опорного колебания). Тогда дифференци­альное уравнение простейшей системы ФАПЧ без ФНЧ имеет вид

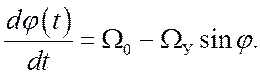                                      (13)

Построенный в соответствии с уравнением (13) фазовый портрет системы для случаев   (кривая 1) и  (кри­вая 2) представлен на рис.12.

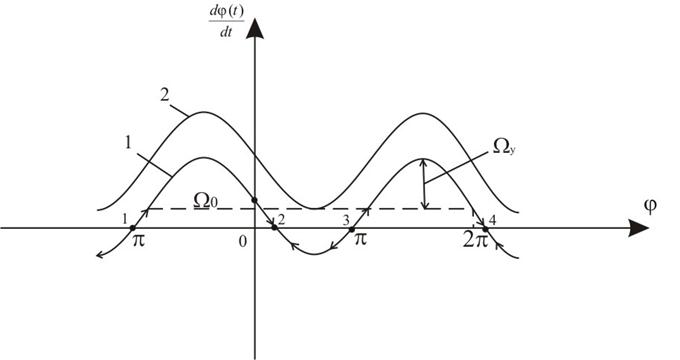
Рис. 12 – Фазовый портрет системы ФАПЧ

В верхней части фазовой плоскости изображающая точка движется по фазовой траектории слева направо (фаза увеличи­вается, так как 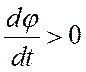). В нижней части – произ­во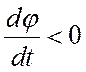дная , поэтому изображающая точка движется справа налево (фаза уменьшается). В точках 1,2,3,4 (кривая 1) производная 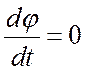 (частотная расстройка отсутствует) и, следовательно, система находится в состоянии равновесия. Однако точками устойчивого равновесия являются только точки 2, 4. Эти точки соответствуют стационарному режиму (режим слежения). Их координаты определяются из соотношения

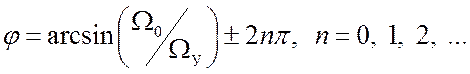
Точки 1 и 3 соответствуют неустойчивому равновесию, так как любое малое возмущение (шум) выводит систему из этого состоя­ния.

Как видно из рисунка, в случае   (кривая 2) производная 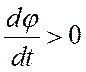  при любых  , то есть режим слежения не возможен. С каждым циклом  изменяется на  радиан (такое явление называют "проскальзыванием" циклов). При этом в системе возникают биения, средняя частота которых равна 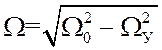 . Появление биений объясняется тем, что максимальное напряжение на выходе ФД ограничено ве­личиной . Поэтому при увеличении расстройки наступает момент, когда управляющее напряжение становится недостаточным для компенсации начальной расстройки и захват сигнала не воз­можен.

Точность системы ФАПЧ в отсутствие шумов характеризуется значением установившейся фазовой ошибки (динамической)

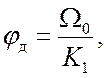                                                       (14)

где   – добротность системы по скорости в с^–1 (система является астатической первого порядка);   – кру­тизна дискриминационной характеристики в В/рад (при использо­вании ФД с характеристикой   численно равен ).

Как свидетельствует анализ фазового портрета системы ФАПЧ без ФНЧ (рис. 3), полоса захвата   численно равна добротности системы  .

Точность системы ФАПЧ в условиях воздействия шумов харак­теризуют дисперсией ошибки

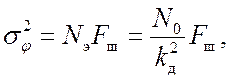                                          (15)

где   – спектральная плотность эквивалентных фазовых флуктуации в рад²/Гц;   – спектральная плотность шума на выходе ФД в Вт/Гц;   – шумовая полоса системы в Гц. ,