Министерство образования Российской Федерации
Красноярский Государственный Технический Университет
Кафедра “Радиотехника”
Лабораторная работа №3
Программная реализация и моделирование РЦФ и НЦФ.
Выполнил: ст-т гр. Р49-1
ИлларионовЮ.С. Проверил:
Глинченко А. С.
Красноярск 2003 г.
Программная реализация и моделирование РЦФ.
Форма реализации фильтра – каскадная.
Число звеньев и значение коэффициентов каскадной формы реализации получены в лабораторной работе №1 с помощью программы РЦФ-СИНТЕЗ и вводятся в программу через файлы, или могут вводиться с клавиатуры.
Граф-схема алгоритма программной реализации РЦФ приведена ниже. Алгоритм обработки представлен в “машинных” переменных B0(J), B1(J), B2(J), A1(J), A2(J) – для коэффициентов звеньев b0J,, b1J , b2J,, a1J , a2J и X, Y, W, W1(J), W2(J) – для отсчетов сигнала x(n), y(n), wJ(n- 1), wJ (n- 2).
C помощью коэффициентов M(J) осуществляется масштабирование входных сигналов звеньев.
%ИСХОДНЫЕ ДАННЫЕ:
fc=900; %Частота входного сигнала
fz1=700;
fz2=1100;
wz1=2*pi*fz1;
wz2=2*pi*fz2;
w=2*pi*fc;
fd=9600; %Частота дискретизации
Td=1/fd; %Период дискретизации
Um1=1; %Амплитуда входного сигнала
t=0:Td:2;
x=Um1*sin(w*t); %Тип входного сигнала
%x=Um1*[sin(w*t)+sin(wz1*t)+sin(wz2*t)]; %Тип входного сигнала
L=7; %Количество звеньев РЦФ
%Коэффициенты РЦФ каскадной формы реализации:
b0(1)= 1; b1(1)= 0; b2(1)=-1; a1(1)= -1.7053279; a2(1)= 0.97579231;
b0(2)= 1; b1(2)= 0; b2(2)=-1; a1(2)= -1.5721759; a2(2)= 0.97115381;
b0(3)= 1; b1(3)= 0; b2(3)=-1; a1(3)= -1.5476164; a2(3)= 0.92233065;
b0(4)= 1; b1(4)= 0; b2(4)=-1; a1(4)= -1.6573186; a2(4)= 0.93232404;
b0(5)= 1; b1(5)= 0; b2(5)=-1; a1(5)= -1.6101947; a2(5)= 0.90039924;
b0(6)= 1; b1(6)= 0; b2(6)=-1; a1(6)= -1.5482331; a2(6)= 0.89258766;
b0(7)= 1; b1(7)= 0; b2(7)=-1; a1(7)= -1.5712516; a2(7)= 0.88568213;
%Масштабные множетили:
M(1)=0.00951979689;
M(2)=0.100250243;
M(3)=0.0486930282;
M(4)=0.0755866096;
M(5)=0.0610396927;
M(6)=0.0772151323;
M(7)=0.0687037764;
%ПРОГРАММА РЕАЛИЗАЦИИ РЦФ:
W=zeros(1,7);W1=zeros(1,7);W2=zeros(1,7);
for n=1:400
X=x(n);
for j=1:L
W(j)=M(j)*X-a1(j)*W1(j)-a2(j)*W2(j);
Y=b0(j)*W(j)+b1(j)*W1(j)+b2(j)*W2(j);
W2(j)=W1(j);
W1(j)=W(j);
X=Y;
end
y1(n)=Y;
end
figure;
subplot(2,1,1); plot(x(1:400));grid;
subplot(2,1,2), plot(y1(1:400));
%ПРОГРАММА РЕАЛИЗАЦИИ ИХ НЦФ:
f1=fc-200;
w1=2*pi*f1;
f2=fc+200;
w2=2*pi*f2;
N=289;
m=-175;n=1;
for i=1:N
if m<0 | m>0
hd(i)=w1*Td*sin(w1*m*Td)/(pi*w1*m*Td)-w2*Td*sin(w2*m*Td)/(pi*w2*m*Td);
Wb(i)=0.42-0.5*cos(2*pi*n/(N-1))+0.08*cos(4*pi*n/(N-1));
h(i)=hd(i)*Wb(i);
m=m+1;n=n+1;
else
hd(i)=w1*Td/pi-w2*Td/pi;
Wb(i)=0.42-0.5*cos(2*pi*n/(N-1))+0.08*cos(4*pi*n/(N-1));
h(i)=hd(i)*Wb(i);
m=m+1;n=n+1;
end
end
figure;
subplot(1,1,1), plot(h(1:289),'b');
%ПРОГРАММА РЕАЛИЗАЦИИ НЦФ:
X=zeros(1,N);
n=2;
for i=1:N
s=x(i);
X(i)=s;
Y=0;m=1;
for j=1:n-1
Y=Y+h(m)*X(n-m);
m=m+1;
end
y2(i)=0.9*Y;
n=n+1;
end
figure;subplot(2,1,1); plot(x(1:289));
subplot(2,1,2), plot(y2(1:289),'b');
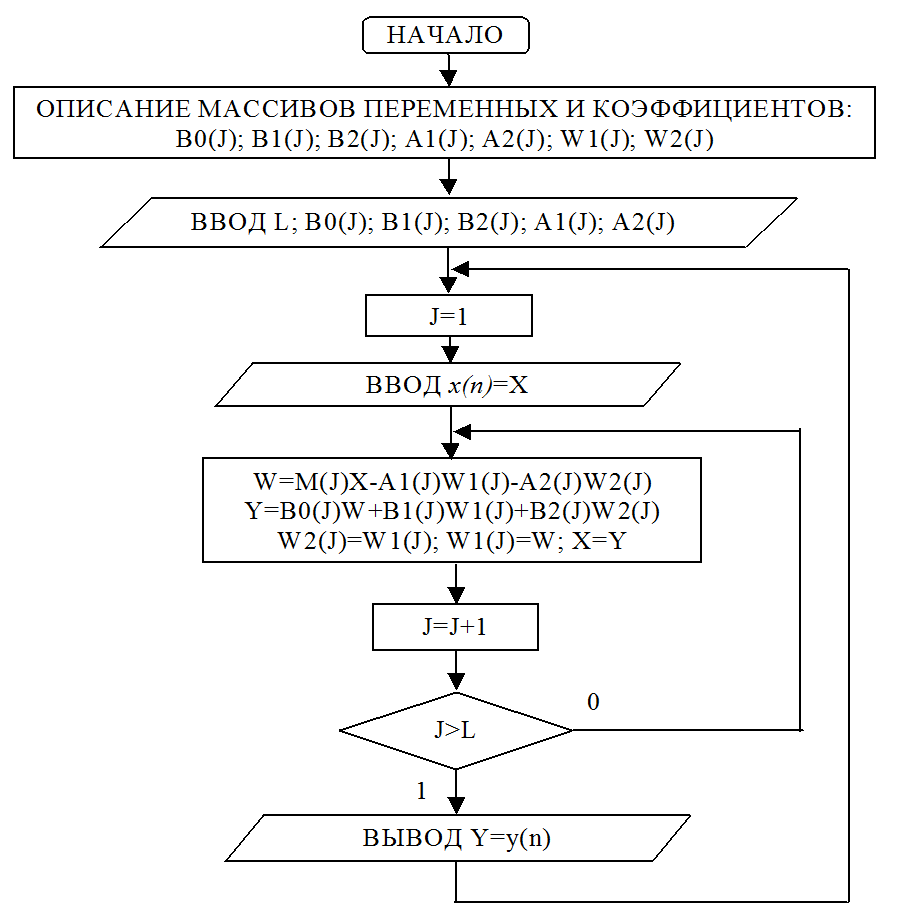
Графики входного и выходного сигнала РЦФ.
Тип входного сигнала – гармоническое колебание с центральной
частотой fо = 900 Гц
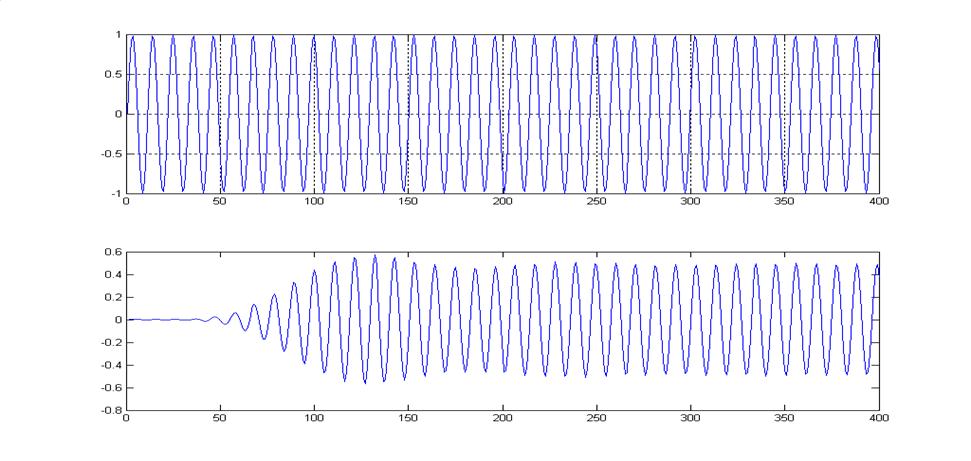
Тип входного сигнала – полигармонический с частотами fо = 900 Гц,fз1 = 700 Гц,fз2 = 1100 Гц.
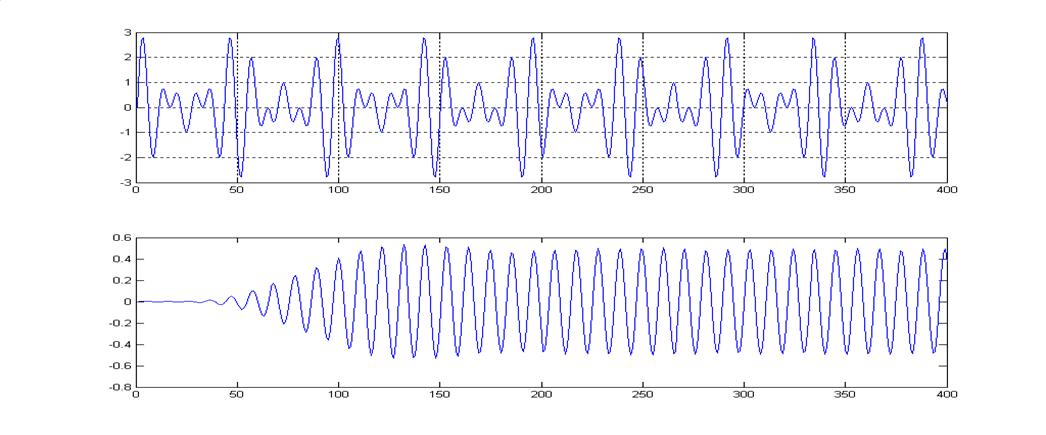
Графики входного и выходного сигнала РЦФ.
Тип входного сигнала – гармоническое колебание с частотой fz1 = 700 Гц
Программная реализация и моделирование НЦФ.
Форма реализации фильтра – на основе ДВС.
Сначала найдём импульсную характеристику НЦФ. Идеальная импульсная характеристика НЦФ для ППФ определяется:
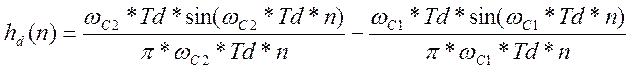
где n
=![]()
![]() - частоты среза;
- частоты среза;
Td – период дискретизации;
N = 123 – длина ИХ, определяется в лабораторной работе №2;
Однако ИХ идеального фильтра
имеет бесконечную длину и не отвечает условию физической реализуемости: при n<0 hd(n)![]() - отклик опережает входное
воздействие. Поэтому она не может быть использована в качестве ИХ НЦФ. Получить
физическую реализуемость можно путём сдвига hd(n) вправо на (N-1)/2 отчётов и
усечением её за пределами n<0 и n
- отклик опережает входное
воздействие. Поэтому она не может быть использована в качестве ИХ НЦФ. Получить
физическую реализуемость можно путём сдвига hd(n) вправо на (N-1)/2 отчётов и
усечением её за пределами n<0 и n![]() N с помощью весовых функций W(n) конечной длины N.
Усечение эквивалентно умножению ВФ на ИХ сдвинутую вправо на (N-1)/2
отчётов:
N с помощью весовых функций W(n) конечной длины N.
Усечение эквивалентно умножению ВФ на ИХ сдвинутую вправо на (N-1)/2
отчётов:
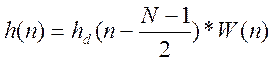
W(n) = Wc(n) – ВФ Блекмана, которая определяется в лабораторной работе №2;
Выходной сигнал НЦФ:
у(n) = 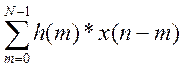
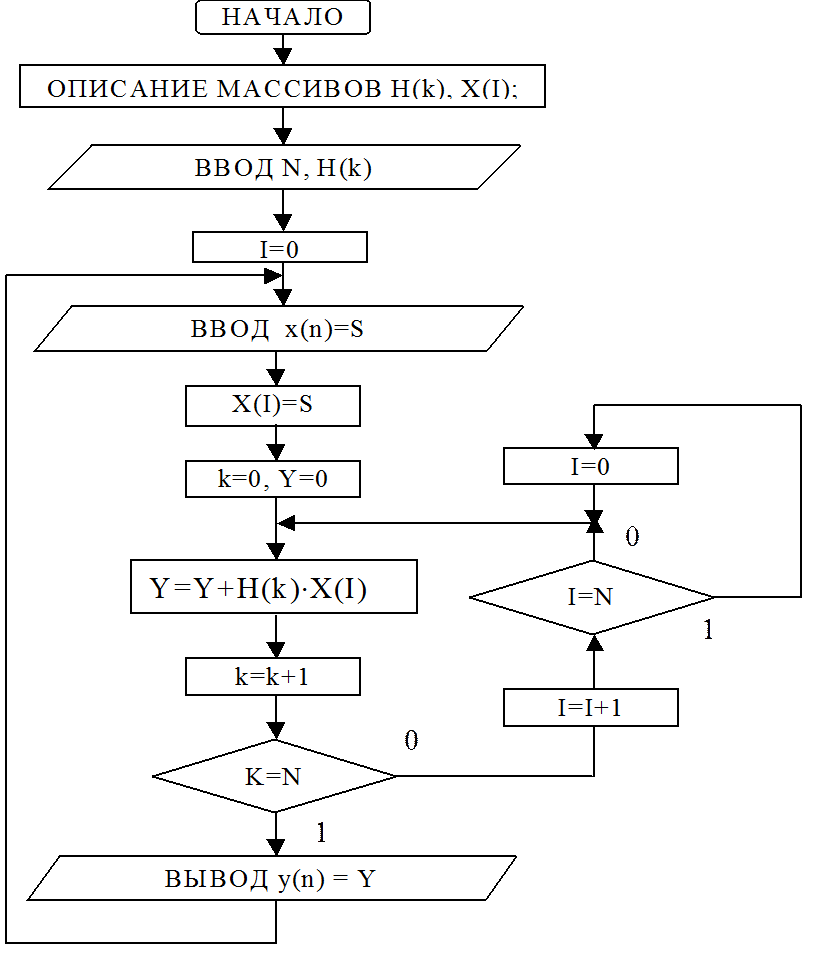
Граф-схема алгоритма программной реализации НЦФ приведена ниже. Алгоритм обработки представлен в “машинных” переменных Y ¬y(n), H(k) ¬ h (m), X(I) ¬ x(n- m). Фильтр реализует базовую операцию Y=Y+H(k)X(I). Переменные X(I) должны быть обнулены при их описании.
Граф-схема алгоритма программной реализации НЦФ
(на основе прямого вычисления ДВС)
%ПРОГРАММА РЕОЛИЗАЦИИ ИХ НЦФ:
f1=fc-200;
w1=2*pi*f1;
f2=fc+200;
w2=2*pi*f2;
N=289;
m=-175;n=1;
for i=1:N
if m<0 | m>0
hd(i)=w1*Td*sin(w1*m*Td)/(pi*w1*m*Td)-w2*Td*sin(w2*m*Td)/(pi*w2*m*Td);
Wb(i)=0.42-0.5*cos(2*pi*n/(N-1))+0.08*cos(4*pi*n/(N-1));
h(i)=hd(i)*Wb(i);
m=m+1;n=n+1;
else
hd(i)=w1*Td/pi-w2*Td/pi;
Wb(i)=0.42-0.5*cos(2*pi*n/(N-1))+0.08*cos(4*pi*n/(N-1));
h(i)=hd(i)*Wb(i);
m=m+1;n=n+1;
end
end
figure;
subplot(1,1,1), plot(h(1:289),'b');
График ИХ НЦФ.
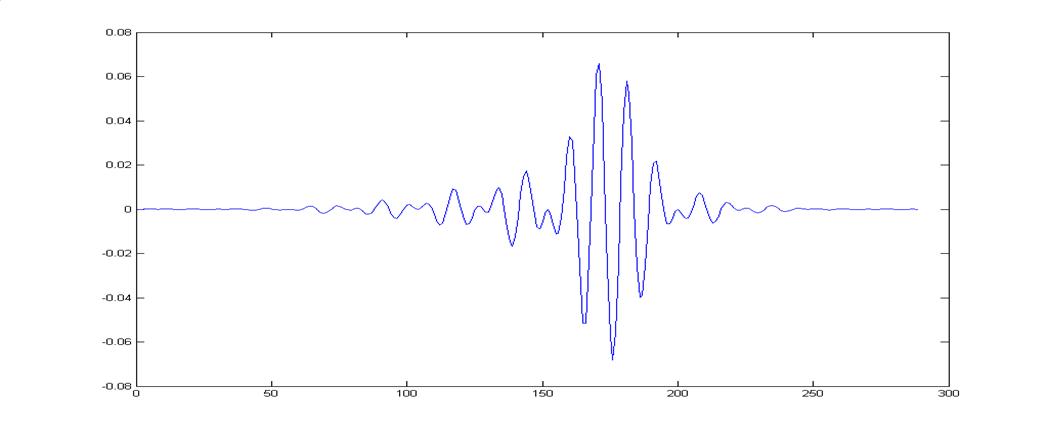
X=zeros(1,N);
n=2;
for i=1:N
s=x(i);
X(i)=s;
Y=0;m=1;
for j=1:n-1
Y=Y+h(m)*X(n-m);
m=m+1;
end
y2(i)=0.9*Y;
n=n+1;
end
figure;
subplot(2,1,1); plot(x(1:289));
subplot(2,1,2), plot(y2(1:289));
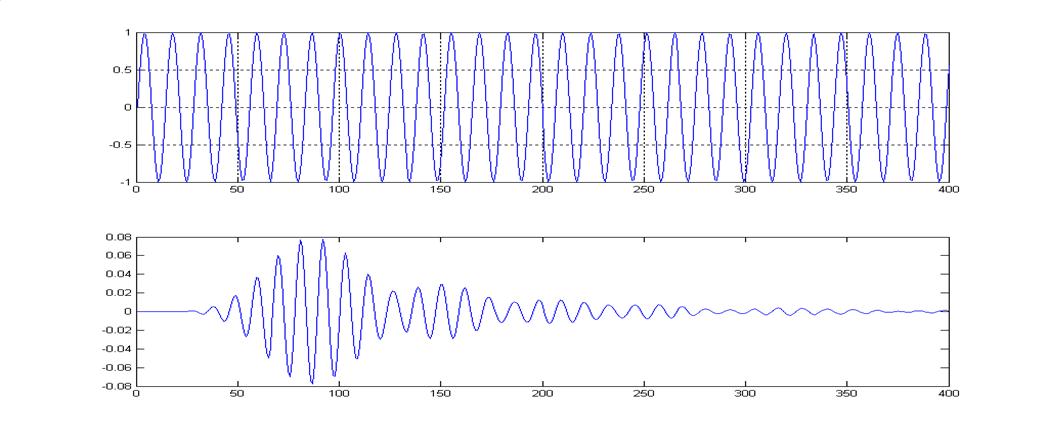
Графики входного и выходного сигнала НЦФ.
Тип входного сигнала – гармоническое колебание с центральной
частотой fо = 900 Гц.
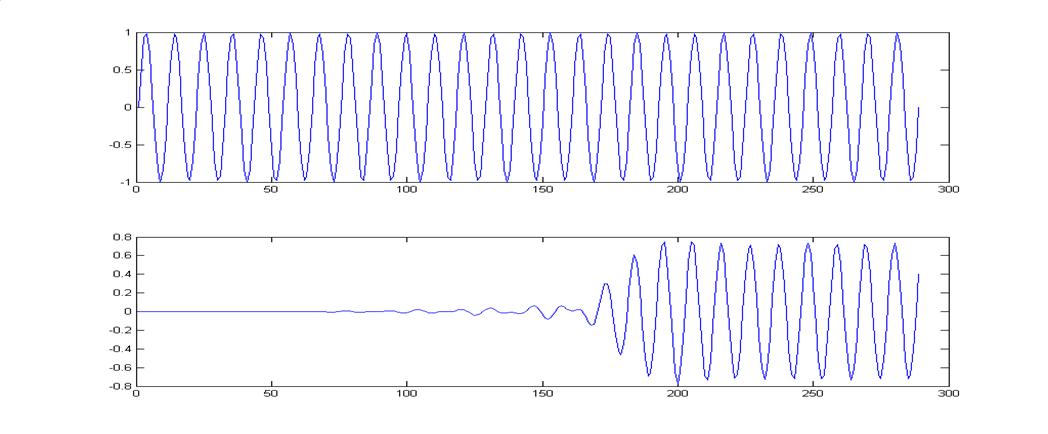
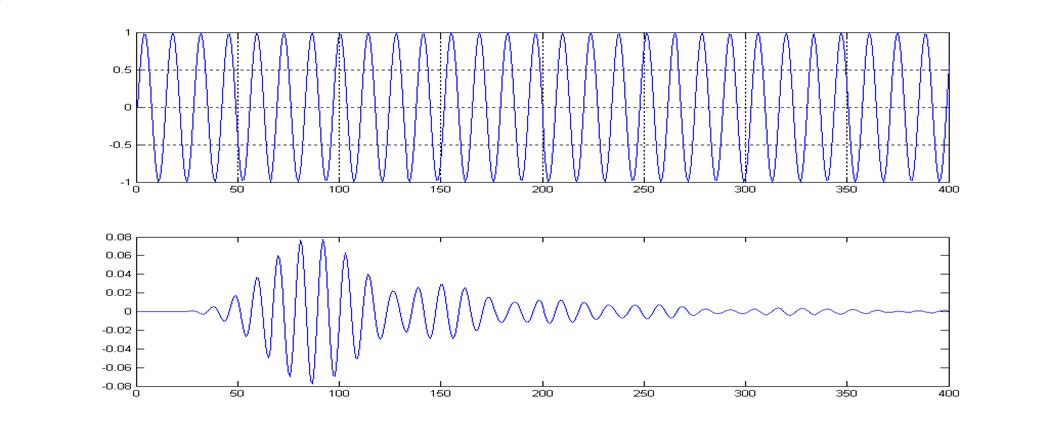
Графики входного и выходного сигнала НЦФ.
Тип входного сигнала – гармоническое колебание с частотой fо = 700 Гц.
Тип входного сигнала – полигармонический с частотами fо = 900 Гц, fz1=700 Гц и fz2=1100 Гц.
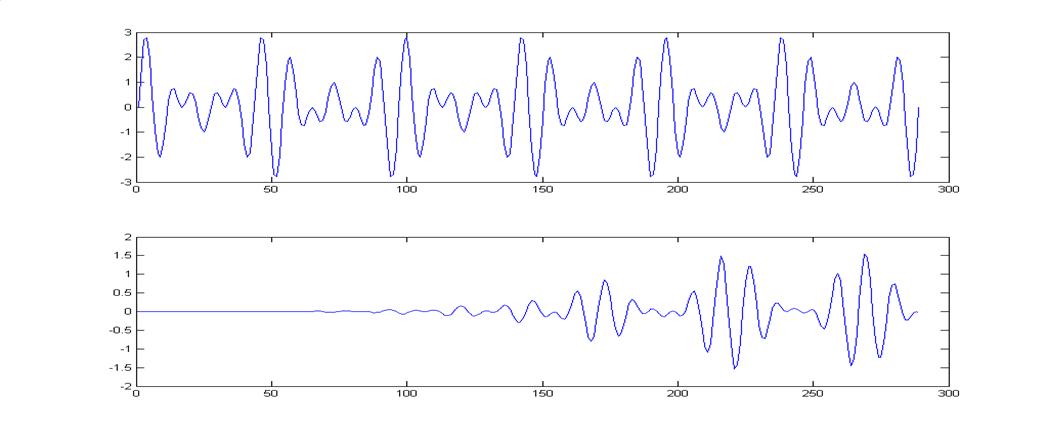
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.