Дисциплина:
ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ
(DSP – digital signal processing)
ПРЕПОДАВАТЕЛЬ:
ПРОФЕССОР КАФЕДРЫ «рАДИОТЕХНИКА»
Глинченко Александр Семенович
виды занятий:
Лекции, лабораторные работы, зачет – 8 семестр,
лабораторные работы, курсовая работа, экзамен – – 9 семестр
Литература:
1. Глинченко, А. С. Цифровая обработка сигналов: Учеб. пособие: В 2 ч. Ч. 1, 2. Красноярск: ИПЦ КГТУ, 2001.
2. Глинченко, А. С. Цифровая обработка сигналов: Учеб. пособие: Красноярск: КрПИ, 1989. (№507)
3. Сергиенко, А. Б. Цифровая обработка сигналов: Учебник для вузов / СПб.: Питер, 2002.
4. Гольденберг, Л. М. и др. Цифровая обработка сигналов: Учеб. пособие/ -М.: Радио и связь, 1990.
5. Гольденберг, Л. М. и др. Цифровая обработка сигналов: Справочник/ -М.: Радио и связь, 1985.
6. Глинченко, А. С. Методические указания по выполнению курсовой и лабораторных работ: №1933, 2076, 2080, 2081.
Лекция 1. 11.02.05.
ВВЕДЕНИЕ В ЦОС
Изучаемые темы:
1. Сигналы и их преобразования при цифровой обработке
2. Цифровые фильтры на основе разностных уравнений и дискретной временной свертки
3. Методы синтеза цифровых фильтров
4. Методы оценки и обеспечения точности цифровых фильтров
5. Цифровые фильтры на основе ДПФ и частотной выборки
6. Специальные задачи и применения цифровых фильтров
7. Методы спектрально-корреляционного анализа сигналов
8. Алгоритмы быстрого преобразования Фурье
9. Методы переноса и преобразования спектров сигналов
10. Многоскоростные системы ЦОС
11. Многоканальные системы ЦОС с частотным разделением сигналов
12. Методы многоканального полосового анализа и синтеза сигналов
13. Методы аппаратно-программной реализации ЦОС
14. Цифровые сигнальные процессоры
15*. Адаптивная обработка сигналов
ТЕМА 1. Сигналы и их преобразования
при цифровой обработке
1.1. Общая структура системы
цифровой обработки аналоговых сигналов
1.2. Дискретизация сигналов по времени
1.3. Спектры дискретных сигналов
1.4. Квантование сигналов по уровню
1.5. Цифровое кодирование сигналов
1.6. *Восстановление сигналов (самостоятельно)
1.7. *Условие математической адекватности дискретного и цифрового сигналов
1.8. *Z-преобразование дискретных сигналов
1.9. *Примеры дискретных последовательностей
1.1 Общая структура системы цифровой обработки аналоговых сигналов
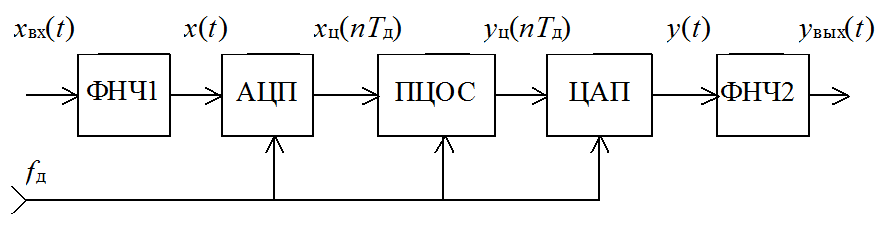
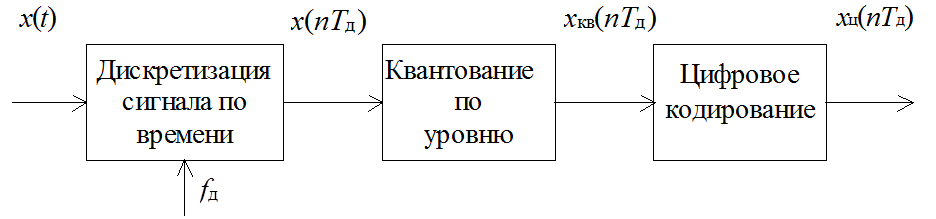
Рис. 1.2. Последовательность операций аналого-цифрового
преобразования сигнала
1.2. Дискретизация сигналов по времени
x(nTд) = x(t)|t = nTд, n = 0, 1, 2, ...;

Рис. 1.3. График аналогового х(t) и дискретного х(nTд) сигналов
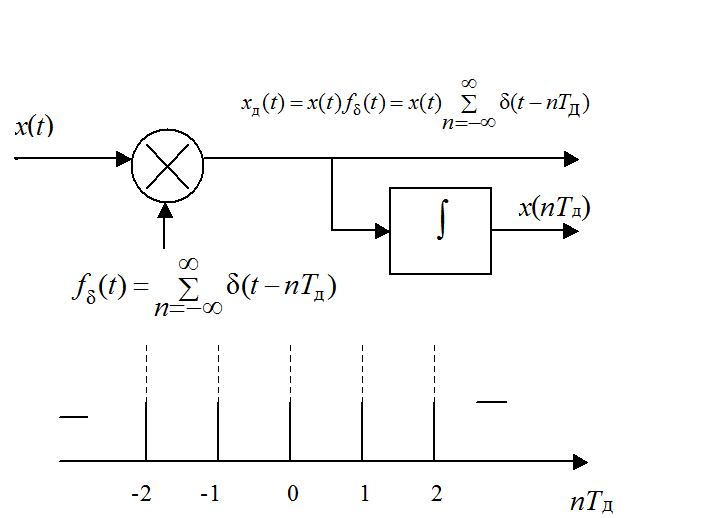
Рис. 1.4. К математической модели дискретизации сигнала по времени
1.3. Спектры дискретных сигналов
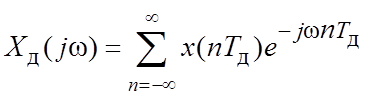 =
= 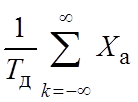 [j(w - kwд)].
[j(w - kwд)].
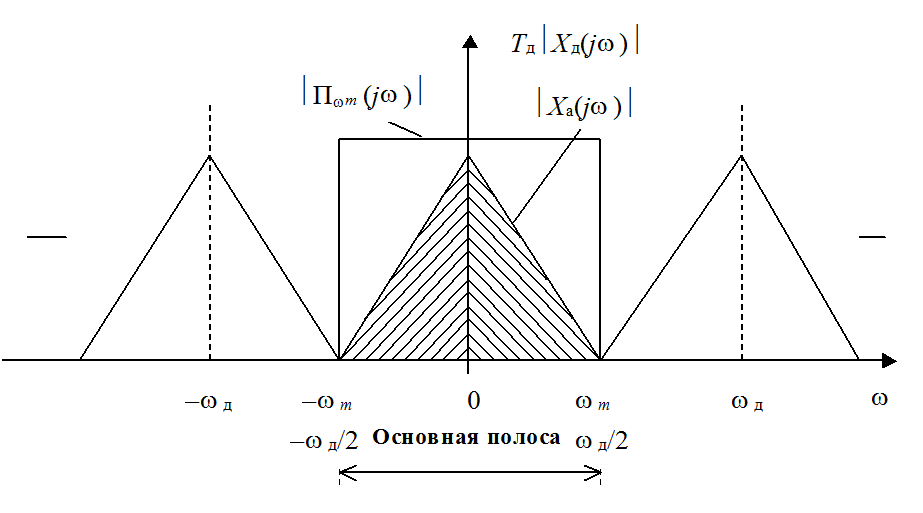 Рис. 1.5. Спектральные преобразования при
дискретизации аналогового сигнала с финитным спектром в случае wд³ 2wm
Рис. 1.5. Спектральные преобразования при
дискретизации аналогового сигнала с финитным спектром в случае wд³ 2wm
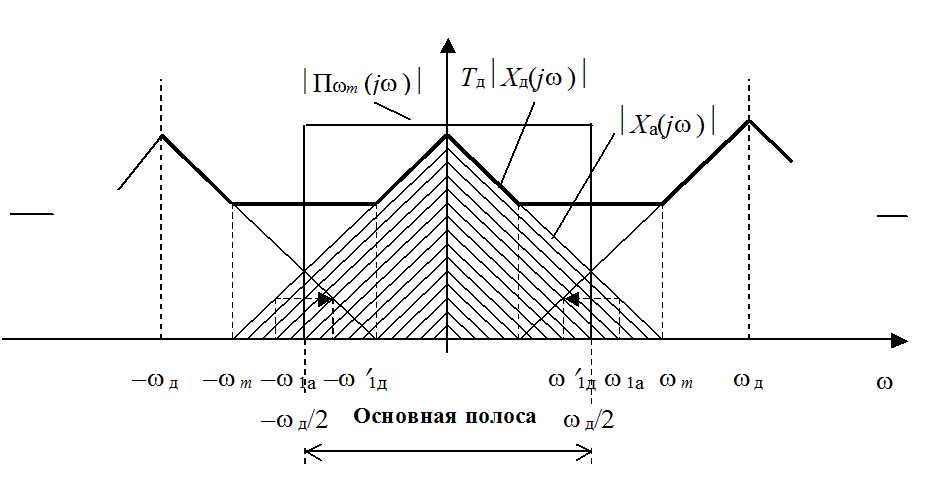
Рис. 1.6 а. Спектральные преобразования при дискретизации
аналогового сигнала с финитным спектром в случае wд< 2wm
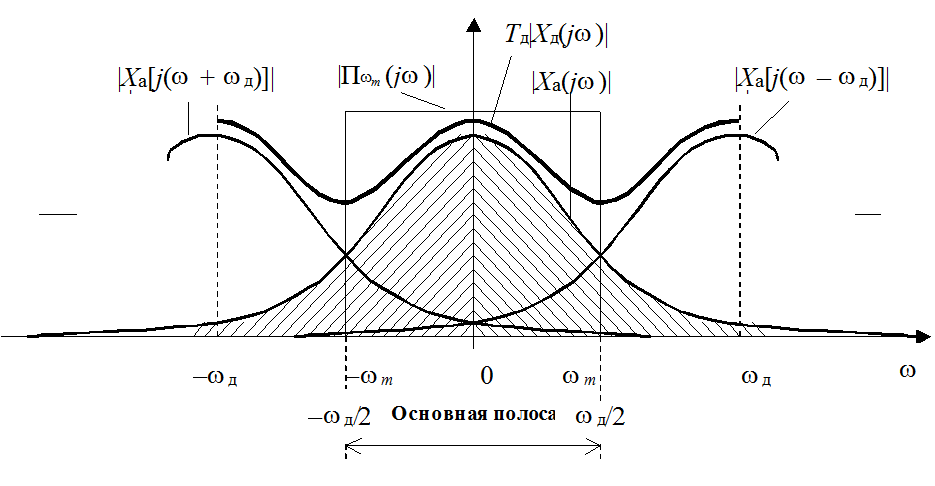
Рис. 1.6 б. Спектральные преобразования при дискретизации аналогового сигнала конечной длительности
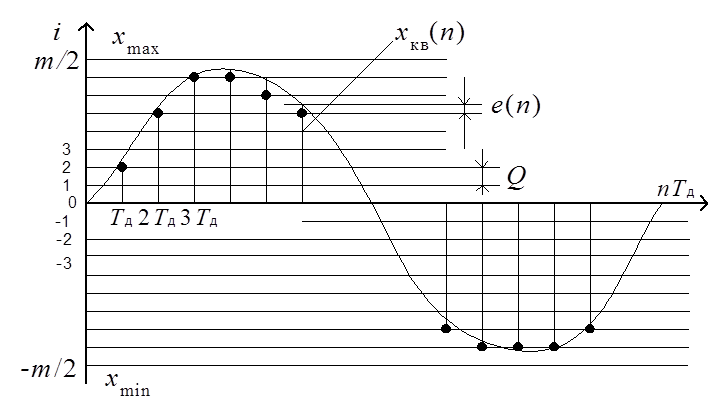
1.4. Квантование сигналов по уровню
хкв(n) = [x(n)/Q]цчQ = iQ ,eкв(n) = хкв(n) -x(n)
1.5. Цифровое кодирование сигналов
хц(цк)(n) = хкв(n)/Q = [x(n)/Q]цч = i(2) – целочисленное
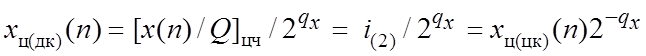 – дробное
– дробное
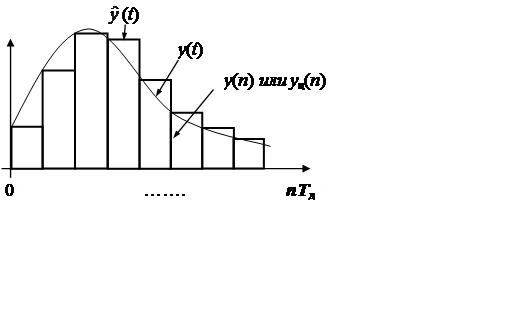
1.6. *Восстановление сигналов (самостоятельно)
 |
1.7. *Условие математической адекватности дискретного и цифрового сигналов
![]() (n)D
(n)D ![]() ц(n)при qх®¥
ц(n)при qх®¥
1.8. *Z-преобразование дискретных сигналов
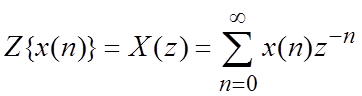
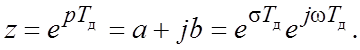
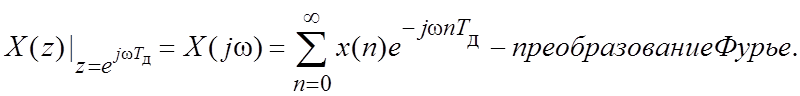
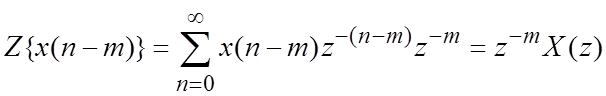
1.9. *Примеры дискретных последовательностей
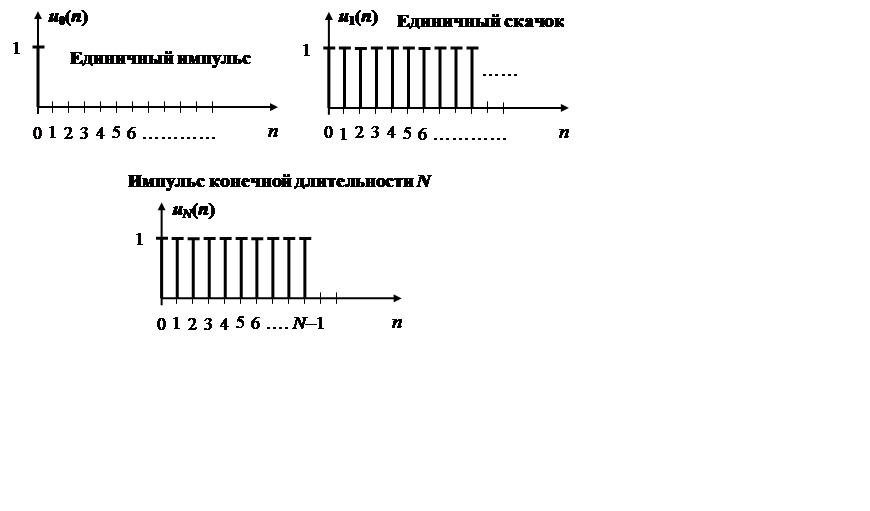 |
Дискретный вещественный гармонический сигнал:
x(n) = Xmcos(wnTд + j), n = 0, 1, 2, …
Дискретный комплексный гармонический сигнал:
x(n) = Xme(jwnTд + j), n = 0, 1, 2, …
Лекция 2. 18.02.05.
ТЕМА 2. Цифровые фильтры
на основе разностных уравнений
и дискретной временной свертки
2.1. Линейная дискретная система (система ЦОС)
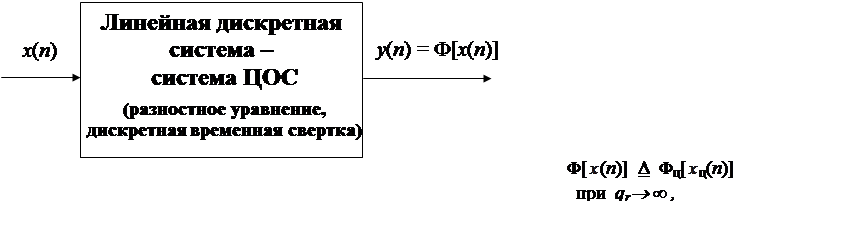 |
2.2. Разностные уравнения (РУ). Рекурсивные и нерекурсивные цифровые фильтры (РФ, НФ)
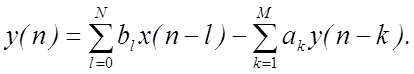
 |
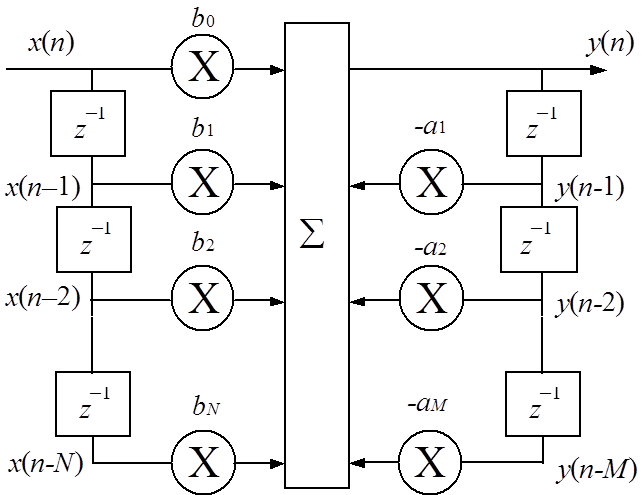
Рис. 2.2. Cтруктура рекурсивного цифрового фильтра, соответствующая прямой форме реализации разностного уравнения;
z–1 – элемент задержки (ячейка памяти)
2.3. Дискретная временная свертка (ДВС),
БИХ- и КИХ-фильтры
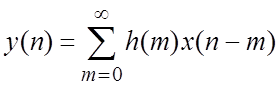
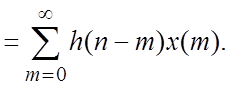
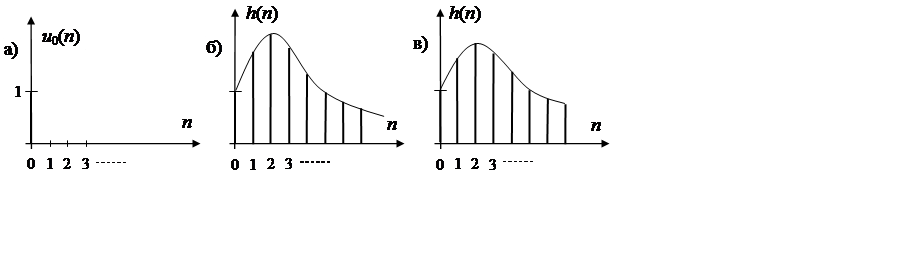 |
Рис. 2.3. Единичный импульс (а),
импульсные характеристики бесконечной (б) и конечной (в) длины
2.4. Передаточная функция ЦФ
H(z)
= Y(z)/X(z);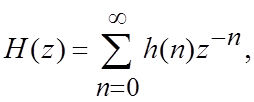
2.5. Частотные характеристики ЦФ
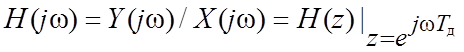 ;
; 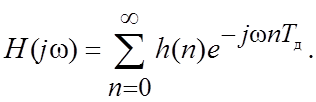
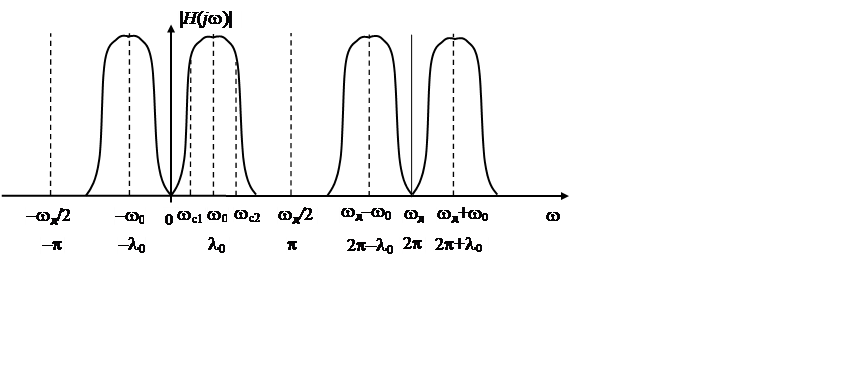 |
Рис. 2.4. Примерный вид АЧХ полосового ЦФ
2.6. Передаточные функции РФ
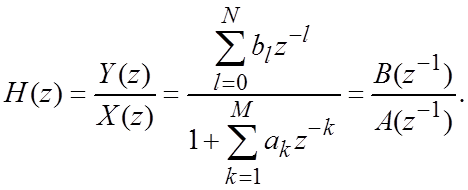
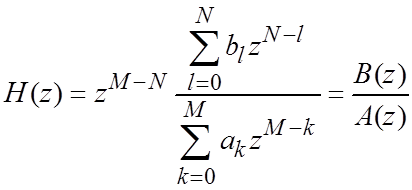 –
полиномиальная форма;
–
полиномиальная форма;
![]() при
при
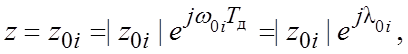
A(z) = 0 при 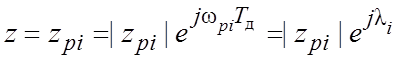 ;
;
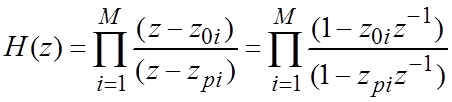 – нуль-полюсная форма.
– нуль-полюсная форма.
Представление передаточной функции
на комплексной Z-плоскости
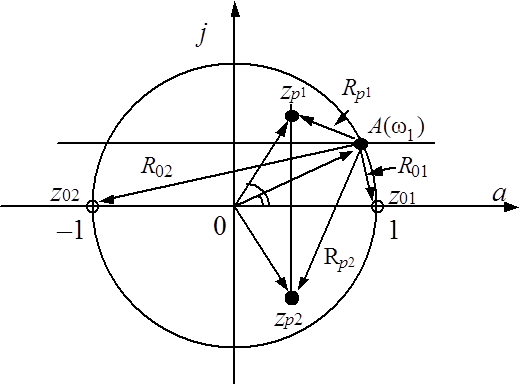
Рис. 2.7. Картина нулей и полюсов ЦФ
2.7. Частотные характеристики РФ
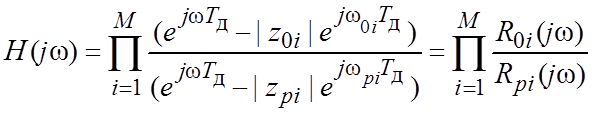
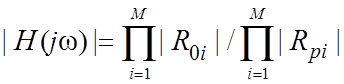 – АЧХ;
– АЧХ; 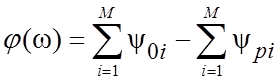 – ФЧХ.
– ФЧХ.
2.8. Формы реализации РФ
а)
Каскадная: 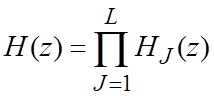 ,
,
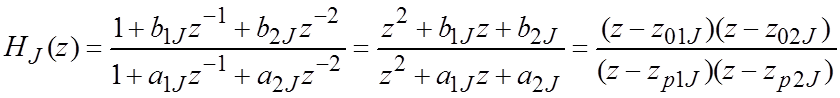
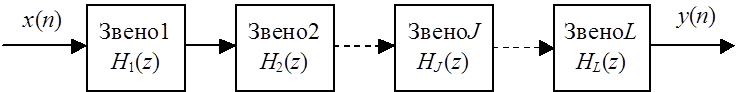
Рис. 2.8. Каскадная структура ЦФ
б) Параллельная: 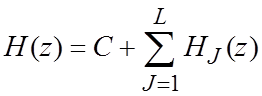 ,
, 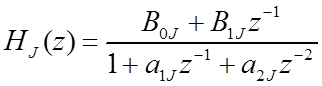 .
.
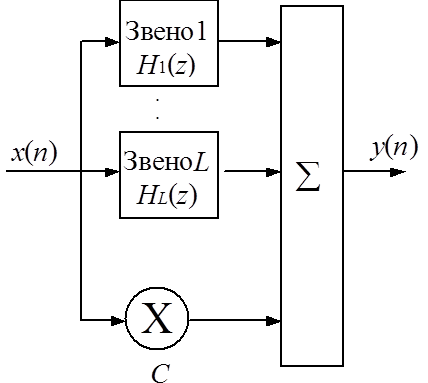
Рис. 2.9. Параллельная структура РФ
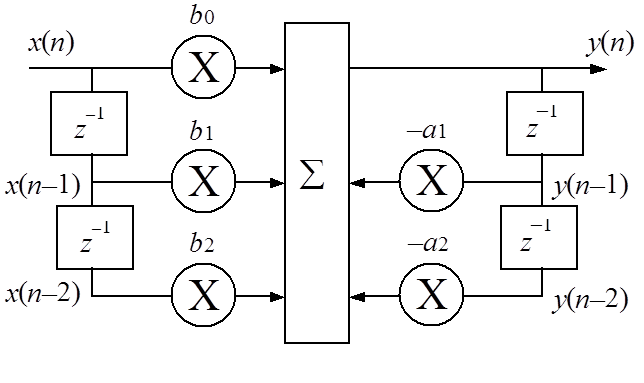
в) Прямая форма реализации звена 2-го порядка
![]()
г) Каноническая форма реализации звена 2-го порядка
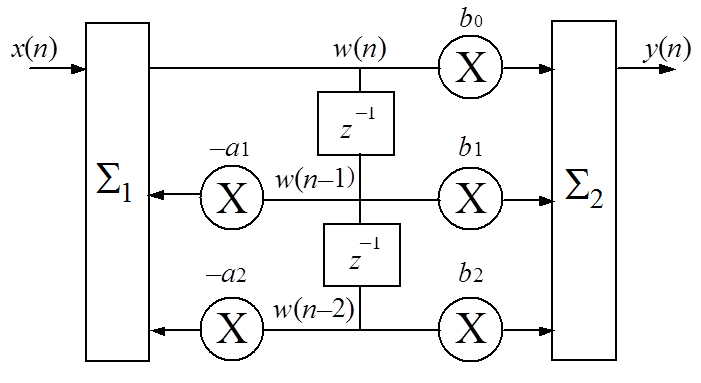
для канонической формы его реализации
![]() ,
, ![]() ,
,
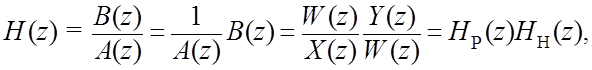
![]() - передаточная функция рекурсивной части звена;
- передаточная функция рекурсивной части звена;
![]() -
передаточная функция нерекурсивной части звена.
-
передаточная функция нерекурсивной части звена.
2.9. Передаточная функция и структура
НФ на основе ДВС
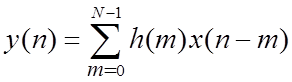 ;
;
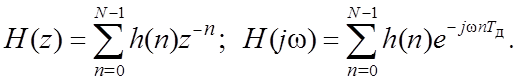
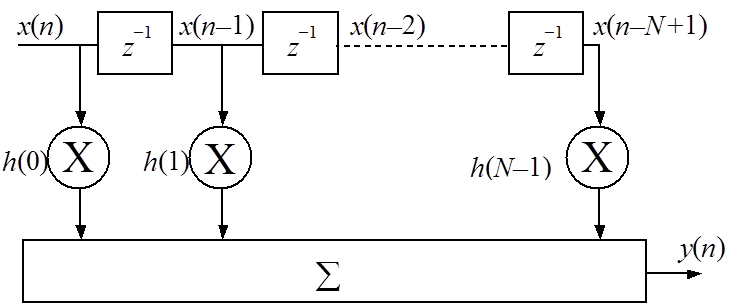
Рис. 2.15. Структурная схема нерекурсивного фильтра на основе ДВС
Лекция3. 25.02.03.
ТЕМА 3. СИНТЕЗ ЦифровыХ фильтрОВ ПО ЗАДАННОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКЕ (ЗАДАЧА АППРОКСИМАЦИИ)
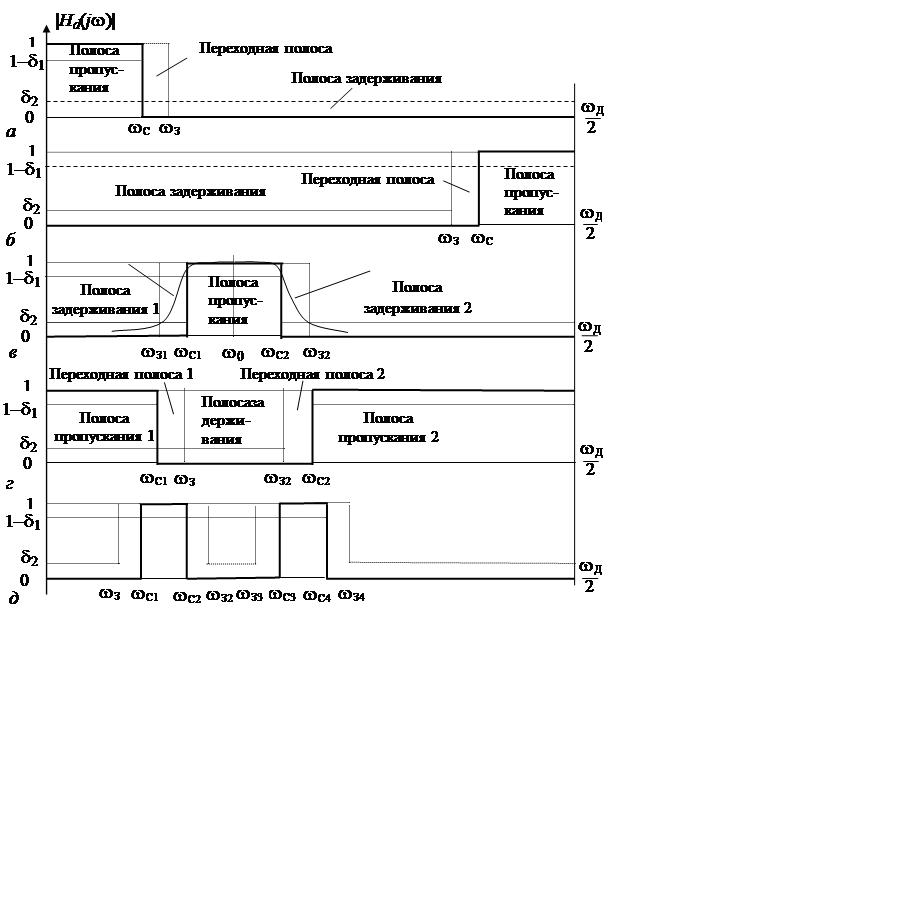 |
Рис. 3.1. Примеры задания АЧХ ЦФ
3.1. Синтез РЦФ по аналоговому прототипу.
Метод билинейного преобразования
АФП: ЦФ: АФП: ЦФ:
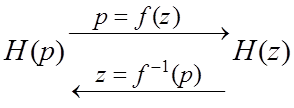 ,
, 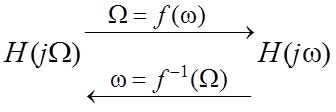 .
.
3.3.2. Простое билинейное преобразование
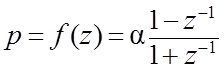 ,
, 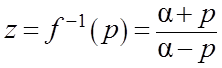 ,
,
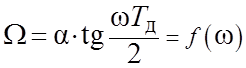 , w = (2/Tд) arctg(W/a)
, w = (2/Tд) arctg(W/a)
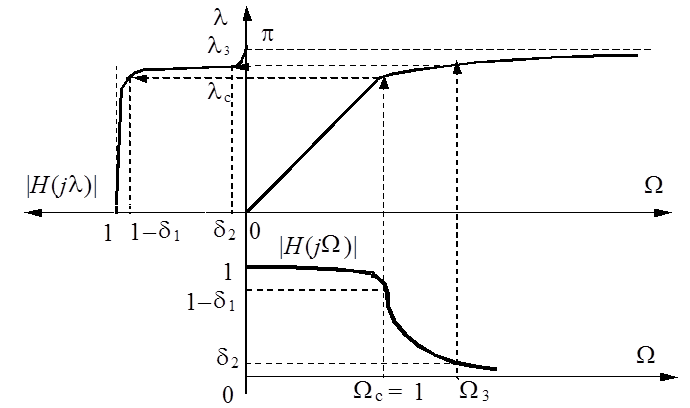
в частотную характеристику цифрового ФНЧ
3.3.3. обобщенное билинейное преобразование
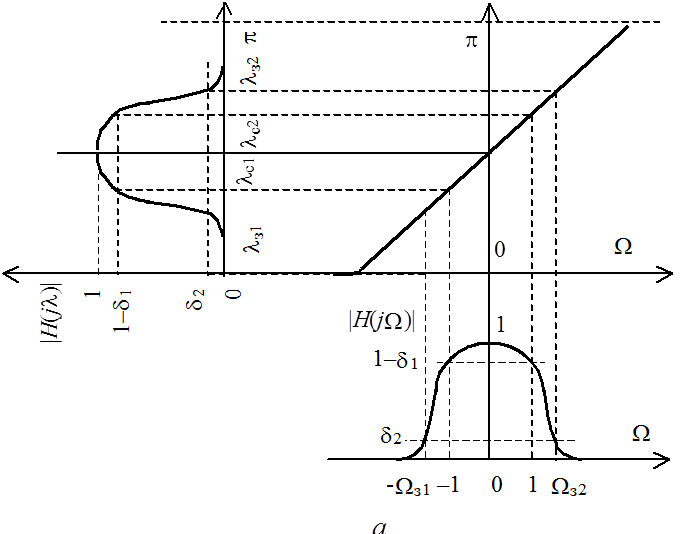
в частотную характеристику цифрового ППФ
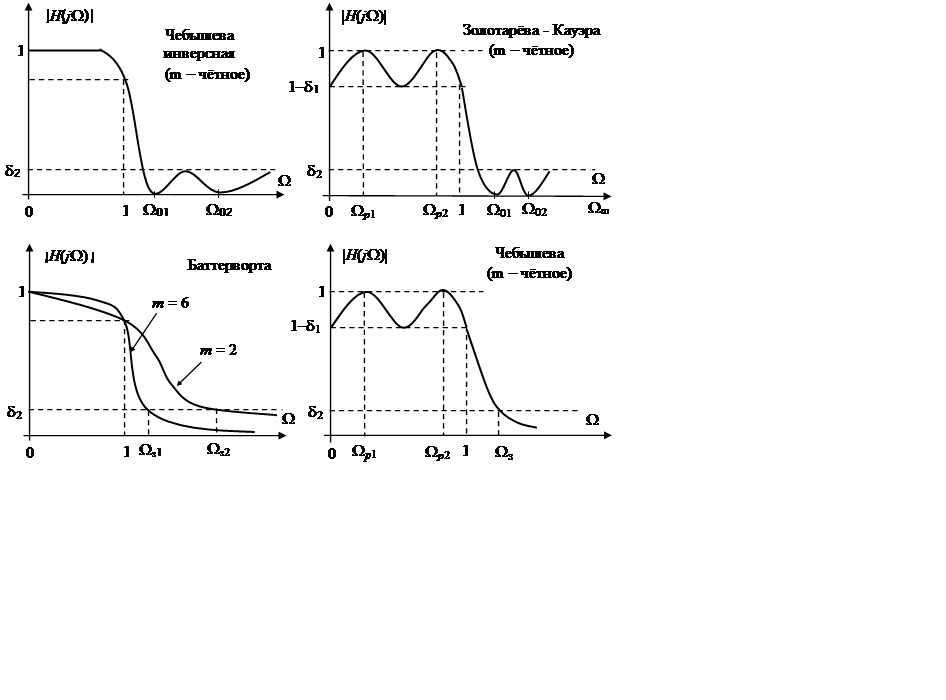 |
Рис. 3.4. Графики частотных характеристик нормализованного АФПНЧ
для различных видов аппроксимации
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.