Одним из путей
преодоления второй из отмеченных трудностей является применение способа
равновесовой поэлементной обработки ШПС, позволяющего организовать ![]() «параллельных» каналов путём их
временного уплотнения. Суть этого способа заключается в поочерёдном вычислении
корреляций каждого элемента принимаемого ШПС с
«параллельных» каналов путём их
временного уплотнения. Суть этого способа заключается в поочерёдном вычислении
корреляций каждого элемента принимаемого ШПС с ![]() элементами
опорного ШПС. При этом устройство поиска является одноканальным, а возможность
организации
элементами
опорного ШПС. При этом устройство поиска является одноканальным, а возможность
организации ![]() «виртуальных» каналов обеспечивается
благодаря увеличению в
«виртуальных» каналов обеспечивается
благодаря увеличению в ![]() раз тактовой частоты
генератора опорной ПСП, сдвигу ПСП на один такт на каждом шаге поиска и
запоминанию результатов равновесовой поэлементной обработки в квадратурных
каналах на интервал, равный длительности элемента ПСП [46]. Описанная процедура
соответствует параллельно-последовательному способу поиска, при котором поиск
осуществляется циклически с «одновременным» анализом
раз тактовой частоты
генератора опорной ПСП, сдвигу ПСП на один такт на каждом шаге поиска и
запоминанию результатов равновесовой поэлементной обработки в квадратурных
каналах на интервал, равный длительности элемента ПСП [46]. Описанная процедура
соответствует параллельно-последовательному способу поиска, при котором поиск
осуществляется циклически с «одновременным» анализом ![]() возможных
значений задержки при общем числе циклов
возможных
значений задержки при общем числе циклов ![]() .
По завершении L-го цикла
принимается решение о значении параметра
.
По завершении L-го цикла
принимается решение о значении параметра ![]() в
соответствии с алгоритмом (2): оценка
в
соответствии с алгоритмом (2): оценка ![]() равна
значению задержки
равна
значению задержки ![]() опорной ПСП, соответствующему
максимальной корреляции.
опорной ПСП, соответствующему
максимальной корреляции.
Анализ помехоустойчивости алгоритма (3) равновесовой поэлементной обработки позволил оценить потери в помехоустойчивости по сравнению с оптимальной корреляционной обработкой (2). Предложенный алгоритм равновесовой обработки обеспечивает практически потенциальную помехоустойчивость (проигрыш не превышает 0.2дБ), позволяя существенно упростить реализацию цифрового устройства поиска сигналов [7].
Проведен сравнительный
анализ помехоустойчивости квазиоптимальных алгоритмов межпериодного накопления
с обратной связью (ОС) и решающей функцией ![]() и
и
![]() . Показано, что при отношении
сигнал/шум на квадратурных выходах коррелятора
. Показано, что при отношении
сигнал/шум на квадратурных выходах коррелятора ![]() 5дБ
указанные алгоритмы практически равноценны по помехоустойчивости (проигрыш
алгоритма со знаковой решающей функцией не превышает 0.2дБ) [11].
5дБ
указанные алгоритмы практически равноценны по помехоустойчивости (проигрыш
алгоритма со знаковой решающей функцией не превышает 0.2дБ) [11].
Дана оценка эффективности
предложенных алгоритмов межпериодного накопления при частично нарушенной
когерентности. Получены зависимости ![]() ,
позволяющие определить предельное значение числа периодов накопления
,
позволяющие определить предельное значение числа периодов накопления ![]() , при котором эффективность
квазикогерентного межпериодного накопления выше, чем некогерентного накопления
(для сигналов РНС диапазона СЧ указанное значение
, при котором эффективность
квазикогерентного межпериодного накопления выше, чем некогерентного накопления
(для сигналов РНС диапазона СЧ указанное значение ![]() )
[10].
)
[10].
Проведен анализ
помехоустойчивости квазиоптимальных алгоритмов поиска МЧМ-ШПС. Получены формулы
для вероятности ошибки (при ![]() )[11]:
)[11]:
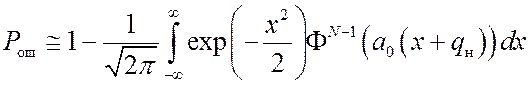
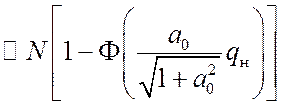 ,
(12)
,
(12)
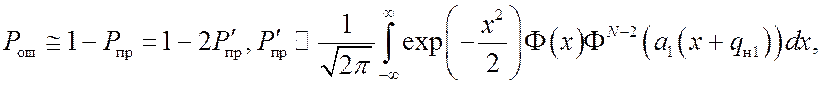
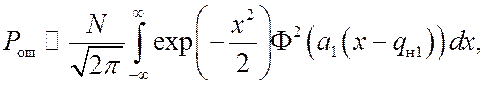 (13)
(13)
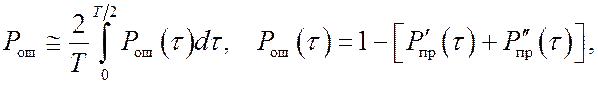
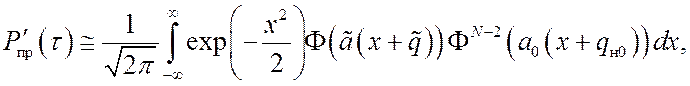
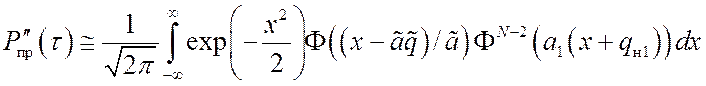 ,
,
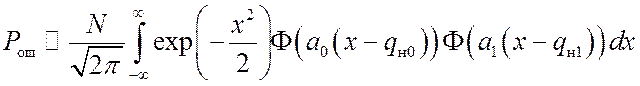 ,
(14)
,
(14)
где ![]() –
интеграл вероятности;
–
интеграл вероятности; ![]() ,
, ![]() ,
, ![]() ,
, ![]() – средние квадратические отклонения модулей корреляции для синхронных
каналов (индексы 0 и 1) и каналов, соответствующих ошибочной синхронизации;
– средние квадратические отклонения модулей корреляции для синхронных
каналов (индексы 0 и 1) и каналов, соответствующих ошибочной синхронизации; ![]() – параметр контрастности синхронных
каналов. Формулы
(12) – (14) соответствуют тем же значениям ошибки
– параметр контрастности синхронных
каналов. Формулы
(12) – (14) соответствуют тем же значениям ошибки ![]() ,
что и формулы (9) – (11).
,
что и формулы (9) – (11).
Анализ зависимостей Pош (q), рассчитанных по формулам (12) – (14), свидетельствует,
что при пороговом отношении сигнал/шум ![]() требуемое
для достижения вероятности
требуемое
для достижения вероятности ![]() число периодов
накопления
число периодов
накопления ![]() [11].
[11].
Время поиска для
описанной процедуры параллельно-последовательного поиска в L раз превышает значение ![]() при оптимальном (параллельном)
способе поиска. Так при
при оптимальном (параллельном)
способе поиска. Так при ![]() и
и ![]() (соответствует
(соответствует ![]() и числу «параллельных» каналов
и числу «параллельных» каналов ![]() ) время поиска
) время поиска ![]() минут, что неприемлемо. Сокращение
времени поиска в 4 раза достигается применением в бортовых станциях
четырехканального приемного устройства (по числу сигналов опорных станций) [26].
минут, что неприемлемо. Сокращение
времени поиска в 4 раза достигается применением в бортовых станциях
четырехканального приемного устройства (по числу сигналов опорных станций) [26].
Исследована
помехоустойчивость системы кодовой синхронизации корреляционного приёмника
периодического МЧМ-ШПС с использованием квазинепрерывного метода анализа
дискретных систем и метода статистического моделирования. Проведён анализ помехоустойчивости предложенных алгоритмов
временного дискриминирования в предположении, что помеха – гауссовский
белый шум. В качестве критерия помехоустойчивости рассматриваемых
алгоритмов используется параметр ![]() характеризующий
увеличение дисперсии эквивалентных временных флуктуаций по сравнению с дисперсией
характеризующий
увеличение дисперсии эквивалентных временных флуктуаций по сравнению с дисперсией
![]() для оптимального временного
дискриминатора. Получены выражения для дискриминационной и флуктуационной
характеристик, а также дисперсии эквивалентных временных флуктуаций для
следующих типов дискриминаторов: оптимального (в отсутствие дополнительной цифровой
модуляции ШПС и при её наличии), квазиоптимальных одно- и двухканального когерентных
дискриминаторов, некогерентного дискриминатора [14].
для оптимального временного
дискриминатора. Получены выражения для дискриминационной и флуктуационной
характеристик, а также дисперсии эквивалентных временных флуктуаций для
следующих типов дискриминаторов: оптимального (в отсутствие дополнительной цифровой
модуляции ШПС и при её наличии), квазиоптимальных одно- и двухканального когерентных
дискриминаторов, некогерентного дискриминатора [14].
Потенциальная
помехоустойчивость алгоритмов
временного дискриминирования МЧМ-ШПС характеризуется дисперсией эквивалентных
временных флуктуаций ![]() ,
, ![]() ,
что совпадает с известным результатом для дисперсии оценки
,
что совпадает с известным результатом для дисперсии оценки ![]() максимального правдоподобия (с
учётом того, что эффективная ширина спектра МЧМ-ШПС
максимального правдоподобия (с
учётом того, что эффективная ширина спектра МЧМ-ШПС ![]() ).
Сравнительный анализ квазиоптимальных
алгоритмов, использующих решающую функцию
).
Сравнительный анализ квазиоптимальных
алгоритмов, использующих решающую функцию ![]() или
или
![]() вместо функции
вместо функции ![]() в оптимальном алгоритме (6)
показывает, что при пороговом отношении сигнал/шум
в оптимальном алгоритме (6)
показывает, что при пороговом отношении сигнал/шум ![]() наиболее
перспективным является алгоритм со знаковой решающей функцией: проигрыш в
помехоустойчивости по сравнению с оптимальным алгоритмом составляет около 0.1дБ
при минимальных аппаратурных и вычислительных затратах [23]. Оценены потери в помехоустойчивости
наиболее
перспективным является алгоритм со знаковой решающей функцией: проигрыш в
помехоустойчивости по сравнению с оптимальным алгоритмом составляет около 0.1дБ
при минимальных аппаратурных и вычислительных затратах [23]. Оценены потери в помехоустойчивости ![]() , обусловленные заменой оптимальной
корреляционной обработки элементов ШПС на равновесовую обработку. Проигрыш в
помехоустойчивости
, обусловленные заменой оптимальной
корреляционной обработки элементов ШПС на равновесовую обработку. Проигрыш в
помехоустойчивости 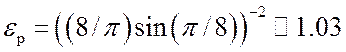 (0.1дБ) и
(0.1дБ) и ![]() (0.9дБ) для алгоритмов с
четырехуровневой и знаковой аппроксимацией [14].
(0.9дБ) для алгоритмов с
четырехуровневой и знаковой аппроксимацией [14].
Результаты статистического
моделирования системы слежения за задержкой (ССЗ) 2-го порядка астатизма,
полученные при числе испытаний ![]() для условий:
начальная ошибка
для условий:
начальная ошибка ![]() (некогерентная ССЗ) и
(некогерентная ССЗ) и ![]() (когерентная ССЗ); отношение
сигнал/шум
(когерентная ССЗ); отношение
сигнал/шум ![]() ; параметры ШПС
; параметры ШПС ![]() ; скорость объекта
; скорость объекта ![]() ; шумовая полоса
; шумовая полоса ![]() – свидетельствуют, что среднее
время синхронизации
– свидетельствуют, что среднее
время синхронизации ![]() , СКО ошибки в
установившемся режиме
, СКО ошибки в
установившемся режиме ![]() и
и ![]() для
некогерентной и когерентной ССЗ соответственно (динамическая ошибка
для
некогерентной и когерентной ССЗ соответственно (динамическая ошибка ![]() ), вероятность срыва слежения
), вероятность срыва слежения ![]() . Для когерентной ССЗ влиянием неидеальности
фазовой синхронизации на помехоустойчивость можно пренебречь, если СКО ошибки
. Для когерентной ССЗ влиянием неидеальности
фазовой синхронизации на помехоустойчивость можно пренебречь, если СКО ошибки ![]() . Сравнение результатов моделирования
с результатами расчета дисперсии
. Сравнение результатов моделирования
с результатами расчета дисперсии ![]() (в установившемся режиме) свидетельствует о приемлемом для
приложений совпадении [23].
(в установившемся режиме) свидетельствует о приемлемом для
приложений совпадении [23].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.