Проведён синтез оптимальных алгоритмов фильтрации МЧМ-ШПС с использованием квазилинейного метода. Получен оптимальный алгоритм временного дискриминирования для системы кодовой синхронизации (СКС) приёмника периодического ШПС с минимальной частотной манипуляцией [19]:
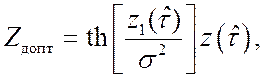
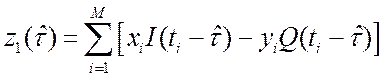 ,
,
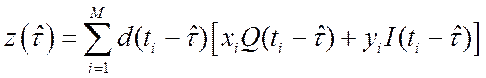 . (6)
. (6)
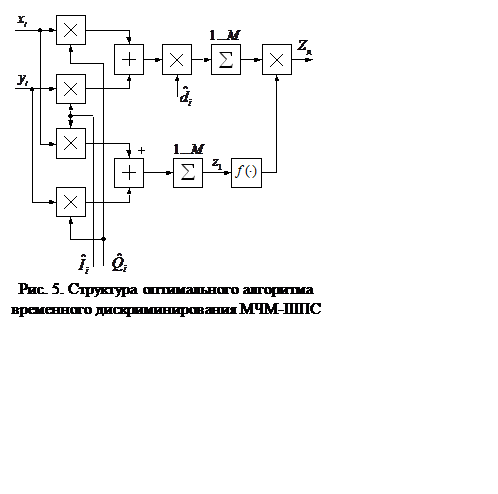 Структура оптимального алгоритма (6)
поясняется схемой рис. 5, где обозначение
Структура оптимального алгоритма (6)
поясняется схемой рис. 5, где обозначение ![]() соответствует
функциональному преобразователю с характеристикой
соответствует
функциональному преобразователю с характеристикой![]() а
а
![]()
![]() ,
, ![]() =
=![]() и
и
![]() =
=![]() –
отсчеты опорных сигналов. Замена характеристики
–
отсчеты опорных сигналов. Замена характеристики ![]() на
на
![]() или
или ![]() приводит
к квазиоптимальным алгоритмам временного дискриминирования.
приводит
к квазиоптимальным алгоритмам временного дискриминирования.
На начальном этапе работы СКС, когда синхронное детектирование принимаемого ШПС невозможно, используется алгоритм некогерентного временного дискриминирования [19]:
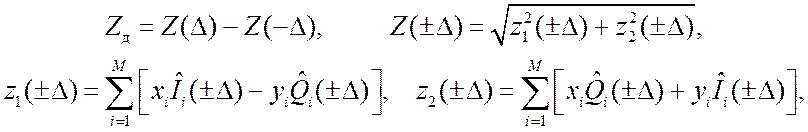 (7)
(7)
где ![]() и
и
![]() – отсчеты опорных сигналов;
– отсчеты опорных сигналов; ![]() и
и ![]() –
квадратурные компоненты корреляции в «опережающем» и «задержанном» каналах
дискриминатора.
–
квадратурные компоненты корреляции в «опережающем» и «задержанном» каналах
дискриминатора.
Структура алгоритма (7) поясняется схемой рис. 6 (подробно показана схема «опережающего» канала). Упрощение оптимального и квазиоптимальных алгоритмов временного дискриминирования достигается за счет равновесовой обработки элементов ШПС в соответствии с (3).
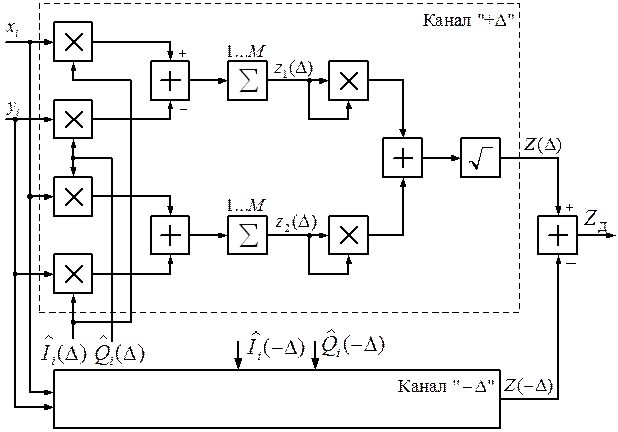
Рис. 6. Структура некогерентного алгоритма временного дискриминирования МЧМ-ШПС
Проведён синтез оптимального алгоритма фазового дискриминирования для системы слежения за фазой периодического ШПС с минимальной частотной манипуляцией [8]:
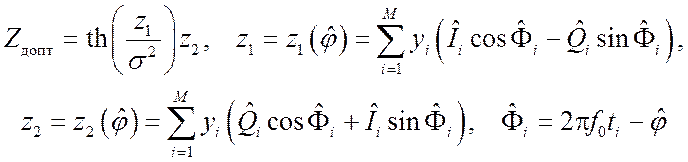 .
(8)
.
(8)
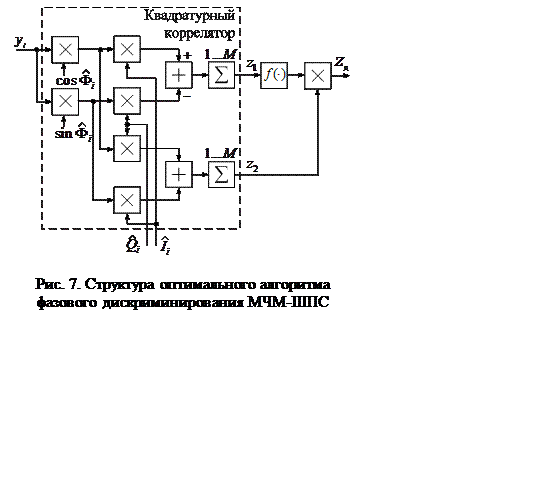 Структура оптимального алгоритма (8)
поясняется схемой рис. 7. В отсутствие цифровой модуляции ШПС характеристика
Структура оптимального алгоритма (8)
поясняется схемой рис. 7. В отсутствие цифровой модуляции ШПС характеристика ![]() . Замена характеристики
. Замена характеристики ![]() функционального преобразователя на
функционального преобразователя на ![]() или
или ![]() приводит
к квазиоптимальным алгоритмам. Отсчеты
приводит
к квазиоптимальным алгоритмам. Отсчеты ![]() и
и
![]() опорных квадратурных видеочастотных
сигналов формируются системой кодовой синхронизации приемника, а отсчеты
опорных квадратурных видеочастотных
сигналов формируются системой кодовой синхронизации приемника, а отсчеты ![]() и
и ![]() опорных
квадратурных сигналов несущей частоты формируются синтезатором системы фазовой
синхронизации (СФС).
опорных
квадратурных сигналов несущей частоты формируются синтезатором системы фазовой
синхронизации (СФС).
Результаты синтеза алгоритмов квазилинейной фильтрации МЧМ-ШПС, в частности дискриминаторов систем кодовой и фазовой синхронизации, с достаточной для приложений точностью совпадают с результатами, полученными с использованием теории нелинейной фильтрации.
Рассмотрена задача синтеза алгоритмов линейной фильтрации параметров МЧМ-ШПС с использованием критерия минимума среднеквадратической ошибки при заданной интегральной оценке переходного процесса. В качестве модели сообщения используется полиномиальная модель, в большинстве случаев достаточно точно описывающая изменение параметров принимаемых сигналов для подвижных морских объектов. С использованием критерия минимума среднего квадрата ошибки получена структура квазиоптимального нестационарного линейного фильтра со «ступенчатой» перестройкой. Предложенный алгоритм нестационарного следящего фильтра, использующий «ступенчатую» перестройку структуры и параметров сглаживающего фильтра, обеспечивает оптимальную фильтрацию параметров МЧМ-ШПС в стационарном режиме, незначительно уступая оптимальному фильтру Калмана в переходном режиме (при существенных преимуществах в реализации).
Способы и устройства приема МЧМ-ШПС с использованием предложенных алгоритмов защищены 5 патентами РФ [42–46].
В четвертой главе проводится анализ помехоустойчивости синтезированных алгоритмов обработки МЧМ-ШПС при воздействии аддитивного гауссовского белогошума.
Оценена помехоустойчивость оптимального и квазиоптимальных алгоритмов поиска с использованием критерия порогового значения qmin отношения сигнал/шум, при котором обеспечивается требуемая точность кодовой синхронизации с заданной вероятностью Pош аномальных ошибок, т. е. ошибок, превышающих по абсолютной величине половину дискрета Δ поиска. Для оптимального алгоритма поиска в отсутствие дополнительной цифровой модуляции ШПС получены формулы для вероятности ошибки [11]:
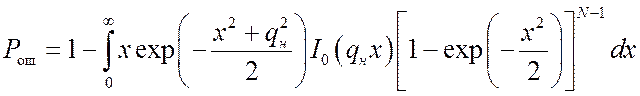
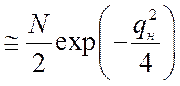 , (9)
, (9)
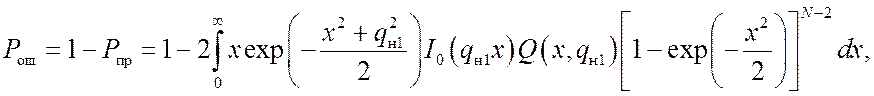
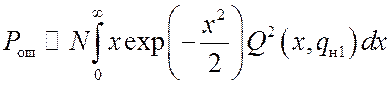 ,
, 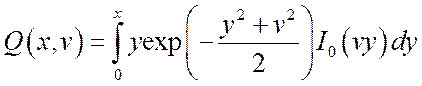 , (10)
, (10)
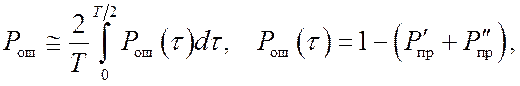
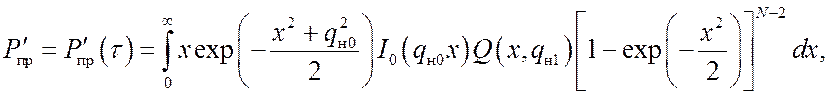
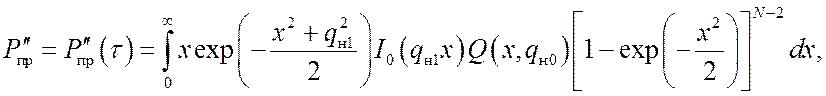 (11)
(11)
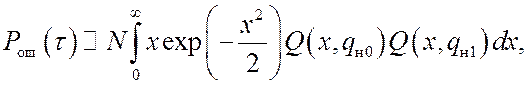
где
I0(x) – модифицированная функция Бесселя
нулевого порядка; ![]() –
Q-функция Маркума (интегральное
распределение Рэлея-Райса).
–
Q-функция Маркума (интегральное
распределение Рэлея-Райса).
Формулы (9)
– (11) получены в предположении, что погрешность ![]() кодовой синхронизации по завершении поиска (при
кодовой синхронизации по завершении поиска (при
![]() ) равна соответственно 0,
) равна соответственно 0, ![]() (при
дискрете поиска
(при
дискрете поиска ![]() ) и является случайной величиной, равномерно
распределенной на интервале
) и является случайной величиной, равномерно
распределенной на интервале ![]() . Параметры
. Параметры ![]() ,
, ![]() и
и
![]() определяют отношение сигнал/шум на квадратурных
выходах «синхронного» канала (
определяют отношение сигнал/шум на квадратурных
выходах «синхронного» канала (![]() ) или каждого из
двух «синхронных» каналов
(
) или каждого из
двух «синхронных» каналов
(![]() ):
):
![]() ,
, ![]() . При
. При ![]() >>1
приближённые формулы практически совпадают с соответствующими точными
формулами, а при конечных значениях
>>1
приближённые формулы практически совпадают с соответствующими точными
формулами, а при конечных значениях ![]() определяют верхнюю
границу для вероятности Pош .
определяют верхнюю
границу для вероятности Pош .
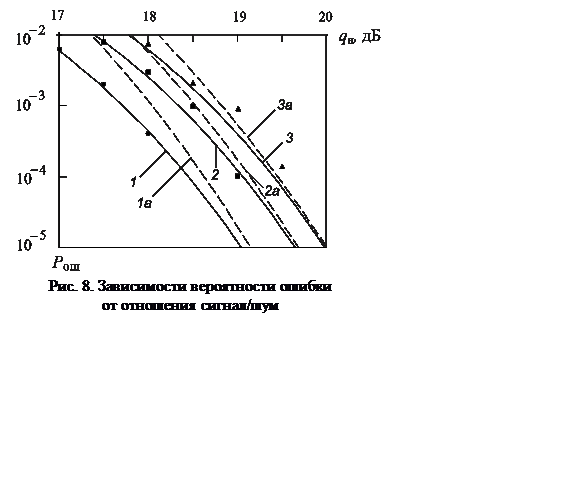 На рис. 8
представлены графики зависимостей вероятности Pош от отношения
сигнал/шум
На рис. 8
представлены графики зависимостей вероятности Pош от отношения
сигнал/шум ![]() при N= 214–1 =
16383, рассчитанные по
формулам (9) – (11) (кривые 1–3 соответствуют точным формулам, а 1а–3а
– верхней границе). Там же представлены результаты статистического
моделирования при числе испытаний 105 (отмечены символами ●, ■, ▲),
подтверждающие аналитические результаты.
при N= 214–1 =
16383, рассчитанные по
формулам (9) – (11) (кривые 1–3 соответствуют точным формулам, а 1а–3а
– верхней границе). Там же представлены результаты статистического
моделирования при числе испытаний 105 (отмечены символами ●, ■, ▲),
подтверждающие аналитические результаты.
Сравнительный анализ
представленных зависимостей позволяет сделать вывод, что при ![]()
![]() дБ точные и приближенные формулы для
вероятности ошибки дают практически одинаковые результаты. Для достижения
приемлемых значений вероятности
дБ точные и приближенные формулы для
вероятности ошибки дают практически одинаковые результаты. Для достижения
приемлемых значений вероятности ![]() требуемое отношение
сигнал/шум
требуемое отношение
сигнал/шум ![]() дБ, что при числе периодов накопления
n =25 соответствует пороговому значению отношения сигнал/шум в полосе
ШПС
дБ, что при числе периодов накопления
n =25 соответствует пороговому значению отношения сигнал/шум в полосе
ШПС ![]() дБ.
дБ.
Практическая реализация
оптимального алгоритма поиска не осуществима по двум причинам: невозможности
когерентного межпериодного накопления результатов корреляционной обработки
вследствие дополнительной цифровой модуляции ШПС; невозможности реализации
параллельного (одновременного) способа поиска при ![]() (в
режиме реального времени).
(в
режиме реального времени).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.