Методы повышения помехозащищенности и точности радионавигационных систем с ограниченным частотным ресурсом, страница 7

,  ,	(3)

где , , . Суммирование по  ведется от  до ; , и ,  для алгоритмов со знаковой и четырехуровневой аппроксимацией.

Структура квазиоптимального алгоритма поиска (рис. 3) отличается от оптимального алгоритма (2) структурой квадратурного коррелятора (3), а также видом решающей функции:  вместо . Обозначения  , , и РБ на рис. 3 соответствуют перемножителю, накапливающему сумматору, функциональному преобразователю с характеристикой  и решающему блоку: показан канал, соответствующий  , , ,  – дискрет поиска,  – число каналов устройства поиска, – априорный интервал значений  (в отсутствие априорных сведений ).

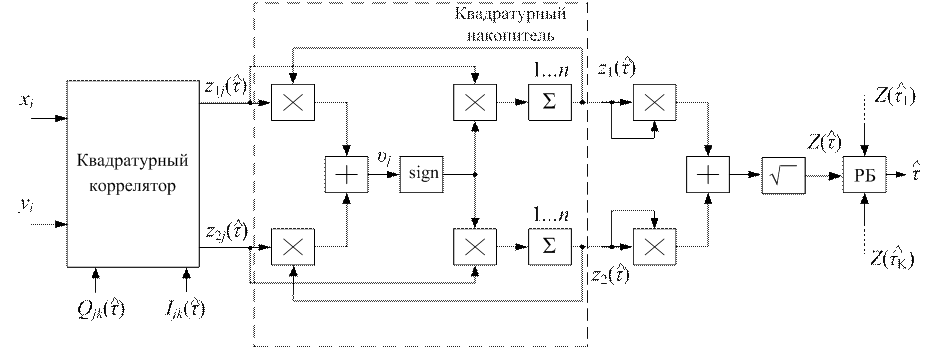
Рис. 3. Структура квазиоптимального алгоритма  поиска МЧМ-ШПС

Предложенный способ равновесовой обработки элементов ШПС сокращает в  раз число операций умножения, необходимых для реализации алгоритма корреляционной обработки, и снижает требования к быстродействию элементной базы. Кроме того, он позволяет реализовать алгоритм многоканального поиска путем последовательного вычисления статистик (3) для  значений задержки (– число «параллельных» каналов) [46].

Рассмотрена задача синтеза оптимальных алгоритмов фильтрации параметров МЧМ-ШПС с использованием  марковской теории нелинейной фильтрации  при гауссовской аппроксимации апостериорной плотности вероятности стационарного марковского процесса . Синтез проводится в предположении, что фильтрация осуществляется оптимальным образом не на всем интервале наблюдения, а лишь в установившемся (стационарном) режиме, что существенно упрощает структуру оптимальных алгоритмов фильтрации. Такой подход к постановке задачи синтеза алгоритмов нелинейной фильтрации наиболее продуктивен для приложений,   т. к. позволяет априори рассчитать коэффициент усиления фильтра и дисперсии оценок, а не пересчитывать эти параметры  в соответствии с текущей оценкой .

Задача синтеза оптимального нелинейного фильтра при сложных моделях сообщения  наталкивается на  значительные математические трудности даже в рамках принятых допущений (отношение сигнал/шум , стационарность фильтра). В связи с этим   синтез алгоритмов нелинейной фильтрации проводится при сравнительно простых моделях сообщения. Это позволяет определить структуру нелинейного фильтра и дискриминатора, которая зависит, главным образом, от вида модуляции и параметров ШПС. Синтез сглаживающих цепей при более сложных моделях сообщения  проводится для выбранной структуры  дискриминатора с использованием теории линейной фильтрации.

          Решена задача нелинейного синтеза  алгоритма фильтрации параметров τ и φ (задержки и фазы) принимаемого МЧМ-ШПС в отсутствие дополнительной цифровой модуляции. В качестве модели сообщения  используется марковский процесс с компонентами, описываемыми априорными стохастическими уравнениями:

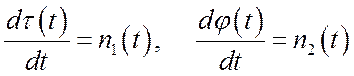,                                        (4а)

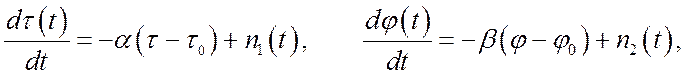           (4б)

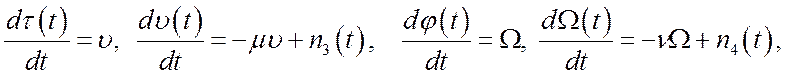      (4в)

где n_i(t) – белый шум с нулевым средним значением и спектральной плотностью N_i/2 (i=1,2,3,4);  τ₀ и φ₀ – известные значения параметров (соответствующие расчетной скорости движения объекта);  – постоянные коэффициенты, характеризующие ширину спектра флуктуаций параметров τ и φ (из-за отличия фактической скорости от расчетной);  – параметры, характеризующие ширину спектра флуктуаций скорости  изменения задержки и частотного сдвига , обусловленных движением объекта.   

          Модель сообщения (4а) соответствует условиям приема сигнала ведущей опорной станции ведомыми станциями (режим автономной синхронизации) или приема сигналов опорных станций неподвижной бортовой станцией: доплеровский сдвиг частоты отсутствует, а флуктуации параметров τ и φ обусловлены собственными шумами опорных генераторов тактовой и несущей частот.

Система уравнений фильтрации для рассматриваемой задачи:

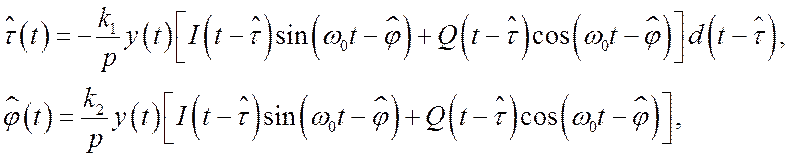         (5)

где  – оценки параметров,   – коэффициенты усиления.

Структура алгоритма (5) фильтрации представлена схемой рис. 4, где обозначения ФОС1 и ФОС2 соответствуют формирователям опорных сигналов: квадратурных видеочастотных сигналов 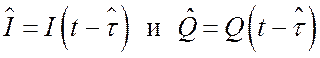 и квадратурных сигналов несущей частоты . Оптимальный фильтр содержит две астатические следящие системы, связанные между собой перекрестными связями: оценки  используются в обоих контурах слежения при формировании опорных сигналов.

         

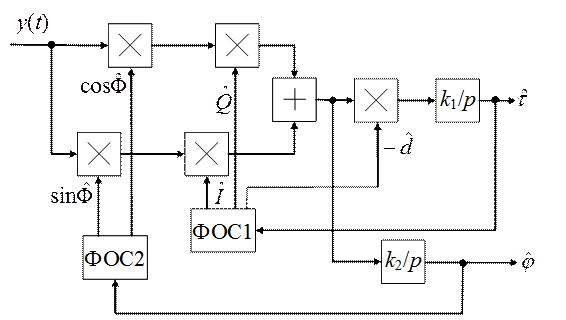
Рис. 4. Структура алгоритма фильтрации МЧМ-ШПС в отсутствие

цифровой модуляции и доплеровского сдвига

Уравнения (4б) описывают изменение параметров τ и φ с учетом как нестабильности частоты опорных генераторов, так и доплеровских составляющих задержки и фазы (случайных компонент) и соответствуют  приему сигналов опорных станций движущейся бортовой станцией при условии, что скорость ее движения определяется автономным датчиком (известна с конечной точностью). Структура алгоритма  фильтрации для этого случая, а также для модели (4в) сообщения с флуктуирующими скоростью изменения задержки и частотным сдвигом  отличается от  схемы  рис. 4  наличием дополнительных звеньев с соответствующими передаточными функциями  для систем слежения за задержкой и фазой ШПС.

          Рассмотрена задача фильтрации задержки и фазы периодического МЧМ-ШПС с дополнительной фазовой манипуляцией, используемой для передачи цифрового сообщения   Для модели (4а) флуктуирующих задержки и фазы получен алгоритм фильтрации, в котором оценка  используется для «снятия» инверсной модуляции «сигналов» ошибки, формируемых дискриминаторами систем слежения за задержкой и фазой ШПС.

Проведён синтез алгоритма фильтрации МЧМ-ШПС с учетом функциональной связи фазы и задержки, определяемой соотношением

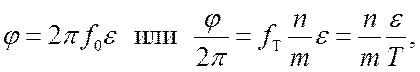
где  – составляющая задержки, определяемая дробной частью периода  несущей ,  а   – целое число периодов Т₀  (число фазовых циклов несущей); ,  – целые. Синтез проведен при условии, что флуктуирующая фаза описывается стохастическим дифференциальным уравнением (4а). Структура алгоритма фильтрации отличается от  схемы  рис. 4  структурой  контура слежения за задержкой, который содержит блок оценки, определяющий статическую ошибку , а также  фильтр нижних частот вместо интегратора (статическая система слежения) [46].