Методы оптимизации (Введение к учебному пособию)

"В  мире не  происходит ничего, в чем

не  был бы  виден смысл какого-либо

максимума или минимума" - Л. Эйлер

Введение

Целью учебного пособия является знакомство с основными методами поиска решений различных экстремальных задач. Математические методы оптимизации применялись и применяются в настоящее время в конечном счете для улучшения конструирования и управления техническими и организационными системами.

Обратимся к рис. 1. Все методы оптимизации можно условно разделить на две группы: методы минимизации функций конечного числа переменных и методы оптимизации динамических систем (методы минимизации функционалов).

К первой группе отнесем классические методы анализа функций, методы нелинейного, линейного, целочисленного, стохастического и динамического программирования.

Рассмотрим несколько примеров. Однако, прежде заметим, что общий путь решения задач, в которых используются методы оптимизации, следующий:

1) осуществляется общая постановка задачи: описывается объект исследования и хотя бы в описательной форме формулируются желания исследователя на выбор наилучшей стратегии;

2) составляется математическая модель объекта;

3) математически формулируются желания исследователя, т.е. составляется функция качества; иногда удается математическую модель подставить в функцию качества и получить явную зависимость функции качества от управляющих воздействий, т.е. от возможных стратегий управления объектом; в остальных случаях математическая модель выступает в роли ограничений на управления;

4) составляется критерий оптимальности, который, как правило, заключается в требовании минимума или максимума функции качества по управляющим воздействиям при наличии ограничений;

5) решается экстремальная задача с помощью метода оптимизации.

Пример. Необходимо попасть из поселка  в районный центр , находящийся на дороге. Считаем, что дорога прямая, а из т.  до дороги можно двигаться только по прямой линии. Известно, что: 1) кратчайшее расстояние от т.  до дороги 9 км; 2) расстояние от т.  до т.  - 15 км; 3) скорость движения из т.  до дороги (т.е. по полям) 4 км в час; 4) скорость движения по дороге - 5 км в час.

Необходимо выбрать такой путь движения , т.е. найти такое , чтобы время движения из т.  в т.  было минимальным. Управляющим воздействием в этой задаче является , который имеет естественное ограничение . Управление, лежащее за этими пределами приводит к явно худшим решениям.

Рассчитаем теперь время движения по ломанной

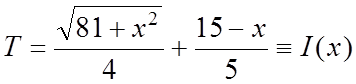. (1)
Получили функцию качества и нам необходимо решить экстремальную задачу

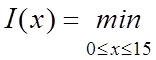.                                                                                                     (2)

Так как  - нелинейная функция от управляющего воздействия , то (2) - это задача нелинейного программирования. Однако, функция  настолько проста, что найти экстремум можно, используя классические методы анализа, которые были полностью развиты уже в XIX в.

В течение длительного времени в экономической науке использовался весьма ограниченный арсенал математических моделей. В частности, широко применялись модели, использующие простейшие алгебраические соотношения и обозначения (см., например, “Капитал” К. Маркса). С помощью них выражены основные экономические закономерности капиталистического хозяйства. Делались также попытки использовать дифференциальное и интегральное исчисление при изучении экономических проблем. Но этот подход в то время (в начале двадцатого столетия) не нашел применения. Основная причина заключалась в том, что исследователи не могли представить всей проблемы в целом: 1) создание адекватной математической модели объекта; 2) решение экстремальных задач с целью получения оптимальных стратегий управления.

Впервые научный подход к решению оптимизационных экономических задач был указан советским математиком ( в последствии академиком) Леонидом Витальевичем Канторовичем. Началом послужило решение в 1938 г. задачи о наилучшей производительной программе загрузки группы лущильных станков в фанерном тресте. После этого в 1938-1939 гг. была решена еще группа задач, например, о раскрое листового материала, распиловка леса и др. При этом много проблем возникало в процессе создания адекватных моделей, а при решении экстремальных задач необходимо было создавать свои методы. Так появилось линейное программирование [1], целочисленное программирование, стохастическое программирование, динамическое программирование, почти полностью изменился арсенал методов нелинейного программирования.

Пример постановки задачи линейного программирования.

Имеется  пунктов, в которых сосредоточен однородный продукт в количествах соответственно  единиц. Его необходимо перевести в  пунктов доставки и в каждом из них должно содержаться единиц продукта. Стоимость перевозки единицы продукта из - го пункта отправки продукта в - ый пункт назначения равна  и она известна для всех комбинаций  индексов.

Обозначим через  - количество продукта, перевозимого по маршруту . Эти величины неизвестны и их нужно выбрать такими, чтобы суммарная стоимость всех перевозок была минимальной.

Запишем общую стоимость всех перевозок

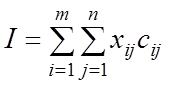
и тогда критерий оптимальности состоит в минимизации функции  по параметрам  с различными наборами индексов

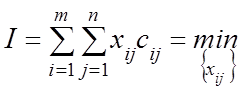.                                                                                         (3)

Выпишем ограничения задачи. Многие из них очевидны. Например,

Кроме того, из -го пункта отправления может быть вывезено только  единиц продукта

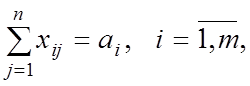                                                                                     (4)
а в  пункт назначения необходимо подвести только  единиц продукта

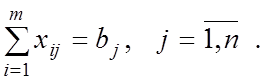                                                                                   (5)
Часто также выполняется условие: общий запас продукта в пунктах отправления равен суммарной потребности в этом продукте пунктов назначения, т.е.

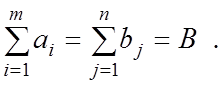
Итак, необходимо удовлетворить критерий оптимальности при наличии всех указанных ограничений. Мы описали простейший вариант так называемой транспортной задачи.

Рассмотрим еще один пример. Отличительной особенностью его является то, что математическая модель задается в сетевой форме, а не в виде привычных нам алгебраических или дифференциальных уравнений.

Охотник движется из пункта  в пункт , проходя ряд промежуточных пунктов. Пункты обозначаем кружками, а возможные пути движения между ними - прямыми линиями (см. рис. 3а). Считаем, что охотник может двигаться только слева направо. На линиях, соединяющими пункты, стоят числа, обозначающие количество дичи, которое  добудет охотник при движении между соответствующими пунктами. Необходимо выбрать маршрут движения, обеспечивающий охотнику максимальную добычу дичи.

Сгруппируем промежуточные пункты по группам 1, 2, 3, 4. В каждую группу входит по 3 пункта. Попробуем решить эту задачу. Самый простой метод - это метод полного перебора всех возможных маршрутов (их ). Для каждого пути необходимо просчитать количество добытой дичи, а затем выбрать оптимальный путь. Очевидно, что при увеличении размерности задачи (количества групп и количества элементов в группе) этот метод требует сравнения астрономически большого числа различных вариантов, например, если в группе  элементов, а число групп равно , то число вариантов будет . При , , . Если перебор вариантов поручить современной быстродействующей вычислительной машине (1 перебор за  сек.), то ей понадобится  лет непрерывной работы.

А теперь решим задачу другим методом. Рассматриваем граф движения охот­ника, начиная с точки , т.е. с конца движения.

В точку  охотник может попасть из одного из трех пунктов 4-ой группы, но так как мы не знаем из какого, то перебираем пункты этой группы.

Если охотник оказался в первом пункте 4-ой группы, то дальнейшее оптимальное движение (такая возможность у него единственная) принесет ему 6 единиц прибыли.  Ставим под пунктом это число, путь также помечаем жирной линией и называем критическим (рис. 3б). Аналогично рассматриваем остальные 2 пункта 4-ой группы.