Затем переходим в пункты 3-ей группы. Если охотник оказался в первом пункте, то дальнейшее движение возможно по трем направлениям, но прежде чем выбрать одно из них, необходимо учесть результат дальнейшего условно оптимального движения из пунктов 4-ой группы. Добавляем к числовым значениям, стоящим над дугами, выходящими из первого пункта, соответственно 6 (для первой дуги), 2 (для второй) и 8 (для третьей). Новые весовые значения дуг записываем рядом со старыми. Они означают, например, что если охотник каким-то образом попал в первый пункт 3-ей группы и затем двигается по первому пути в первый пункт 4-ой группы, а дальнейшее движение оптимально, то он получит прибыль в 6 единиц. Из трех возможных путей движения из первого пункта 3-ей группы выбираем тот, который дает максимум прибыли. Этот путь помечаем и под пунктом ставим максимальную прибыль, соответствующую дальнейшему оптимальному пути движения.
|
|
Аналогичные расчеты проводим для остальных пунктов 3-ей группы (рис. 3в).
|
|
Затем переходим к рассмотрению
пунктов 2-ой группы и т.д., пока не попадаем в ![]() (рис. 3г).
(рис. 3г).
В итоге получаем, что если
двигаться по оптимальному пути из ![]() в
в
![]() , то максимальная прибыль
(количество добытой дичи) равна 23. Оптимальный путь теперь нетрудно получить,
двигаясь из т.
, то максимальная прибыль
(количество добытой дичи) равна 23. Оптимальный путь теперь нетрудно получить,
двигаясь из т. ![]() вправо по
критическим дугам.
вправо по
критическим дугам.
Описанный метод решения носит
название динамическое программирование. Если с его помощью решить
аналогичную задачу, для которой граф движения содержит ![]() групп по
групп по ![]() элементов в каждой, то потребуется
произвести
элементов в каждой, то потребуется
произвести ![]() простейших
операций сложения и сравнения вариантов. Причем, построение каждого варианта
проще, чем в методе полного перебора. При
простейших
операций сложения и сравнения вариантов. Причем, построение каждого варианта
проще, чем в методе полного перебора. При ![]() и
и ![]() величина
величина ![]() и вычислительная машина, выполняя
одну операцию сравнения за
и вычислительная машина, выполняя
одну операцию сравнения за ![]() сек,
решит задачу за 0,02 сек. Сравните с длительностью счета
сек,
решит задачу за 0,02 сек. Сравните с длительностью счета ![]() лет по методу полного перебора.
лет по методу полного перебора.
Метод динамического программированияв настоящее время представляет собой один из эффективных подходов к решению разнообразных классов статических (глава 6) и динамических (глава 9) экстремальных задач.
Вторая группа методов служит для оптимизации динамических систем. Эту группу можно разделить на следующие 3 класса: вариационное исчисление, принцип максимума, динамическое программирование.
Классическое вариационное исчисление включает в себя методы определения минимального или максимального значения функционала без ограничений на искомые переменные, либо при наличии ограничений типа равенств.
Известно, что функционал - это оператор, переводящий пространство функций в пространство чисел. Экстремум функционала обеспечивается за счет подбора функций, которые в вариационном исчислении обычно считают гладкими.
Началом развития вариационного исчисления можно считать 1696 год, когда Иоган Бернулли опубликовал для математиков нерешеннуюзадачу о брахистохроне - линии наискорейшего ската материальной точки. Рассмотрим постановку этой задачи.
|
|
В плоскости ![]() имеются две заданные, не лежащие на
одной вертикальной прямой точки
имеются две заданные, не лежащие на
одной вертикальной прямой точки ![]() (0,0)
и
(0,0)
и ![]() (
(![]() ) (Рис. 4). Необходимо найти линию,
соединяющую их, при движении вдоль которой под воздействием силы тяжести
материальная точка пройдет расстояние между
) (Рис. 4). Необходимо найти линию,
соединяющую их, при движении вдоль которой под воздействием силы тяжести
материальная точка пройдет расстояние между ![]() и
и ![]() за наименьшее время. Силами трения
пренебрегаем.
за наименьшее время. Силами трения
пренебрегаем.
Найдем зависимость времени
движения от траектории ![]() .
Обозначая через
.
Обозначая через ![]() элемент пути, а
через
элемент пути, а
через ![]() элемент времени, можем
записать
элемент времени, можем
записать
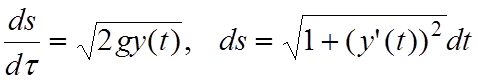 ,
,
где ![]() - ускорение свободного
падения. Подставляем
- ускорение свободного
падения. Подставляем ![]() в
первое уравнение, разделяем переменные и интегрируем "от т.
в
первое уравнение, разделяем переменные и интегрируем "от т. ![]() до т.
до т. ![]() ":
": 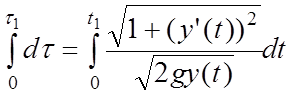 . Отсюда получаем время движения
из точки
. Отсюда получаем время движения
из точки ![]() в точку
в точку ![]()
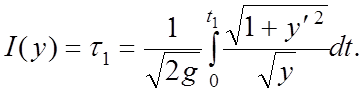 (6)
(6)
Необходимо найти минимум этого
функционала по функции ![]()
![]() при условии, что координаты точек
при условии, что координаты точек ![]() и
и ![]() заданы
заданы
![]() (7)
(7)
Решение этой задачи мы рассмотрим после того, как познакомимся с методами вариационного исчисления (глава 7).
Сразу же после опубликования задачи о брахистохроне она была решена И. Бернулли, Я. Бернулли, Г. Лейбницем, И. Ньютоном и Г. Лопиталем. Эта и другие вариационные задачи решались искусственными методами и несколько позже в работах Л. Эйлера и Ж. Лагранжа разработана общая теория вариационного исчисления.
Вариационное исчисление нашло широкое применение, например, в механике и физике в виде вариационных принципов: принцип наименьшего действия; законы сохранения энергии, количества движения, момента количества движения, импульса; различные вариационные принципы классической и релятивистской теории поля, принцип Ферма в оптике, принцип Кастилиано в теории упругости и др.
Вариационное исчисление также широко используется в автоматическом управлении. Но в автоматическом управлении гораздо чаще возникают задачи при наличии сложных ограничений на управляющие воздействия и переменные, характеризующие движение объекта (фазовые координаты объекта). Эти задачи не могут быть решены в рамках классического вариационного исчисления, потому что искомые переменные негладкие функции.
|
|
Рассмотрим простейший пример. Необходимо перенести точку подвеса маятника из одного места в другое, но так, чтобы амплитуда колебания маятника в конечной точке была равна нулю, а время, затрачиваемое на перемещение, было минимальным. Если задаваться классом гладких решений, как требует этого классическое вариационное исчисление, то потребуется бесконечно большое время на перемещение маятника (ведь в конечной точке колебания маятника должны отсутствовать). Истинное же оптимальное решение задачи имеет релейный вид (см. рис. 5).
Рассмотрим для простоты случай,
когда длина маятника больше половины расстояния от ![]() до
до ![]() .
.
Переместим “мгновенно” точку
подвеса маятника в т.![]() и
ждем пока маятник совершит половину колебания, груз маятника займет положение
на вертикальной прямой, проходящей через т.
и
ждем пока маятник совершит половину колебания, груз маятника займет положение
на вертикальной прямой, проходящей через т. ![]() . В этот момент опять “мгновенно”
перемещаем точку подвеса маятника в т.
. В этот момент опять “мгновенно”
перемещаем точку подвеса маятника в т. ![]() и задача решена.
и задача решена.
Математики быстро откликнулись на возникшее затруднение теории автоматического управления и создали в 1956 году специальные методы оптимизации - принцип максимума (СССР) и динамическое программирование (США).
Принцип максимума был разработан группой молодых советских ученых, которой руководил академик Лев Семенович Понтрягин. Вначале был сформулирован некоторый гипотетический принцип при решении простейшей задачи о максимальном быстродействии. Затем он получил строгое обоснование и дальнейшее развитие.
Аналогичный процесс происходил и с динамическим программированием, создателем которого является крупнейший американский математик Ричард Беллман.
В дальнейшем была установлена общность этих методов и выявлены различия. Оказывается, что большая группа задач может быть решена на основе обоих подходов, но для каждой задачи один из методов обеспечивает меньшие затраты на поиск и реализацию оптимальных управлений. Существуют также классы задач, решаемые только на основе одного из методов. Установлена общность между этими подходами и вариационным исчислением, нелинейным программированием, вариационными методами функционального анализа и др. В результате появились фактически новые методы решения экстремальных задач. Например, в монографии А.И. Пропоя (см. [6] списка литературы к главе 2) разработан новый подход к управлению дискретными динамическими системами, связанный с аппаратом принципа максимума и нелинейным программированием.
Много эффективных, но сравнительно узко направленных методов оптимизации разработано в таких теориях как: теория игр, теория графов, теория массового обслуживания, сетевое планирование, управление запасами. Большинство из них изучается студентами в виде самостоятельных учебных дисциплин, поэтому на этих специальных методах мы останавливаться не будем.
Часть методов оптимизации была разработана сравнительно давно (например, во времена Эйлера была создана классическая теория вариационного исчисления), большая же часть - в последнее столетие. Причем, некоторые методы имеют возраст не более 20 - 40 лет, некоторые - создаются в настоящее время (например, методы глобальной оптимизации), а большая их часть еще не известна.

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.