Михаил Петрович Медиченко.
Радиотехнические цепи и сигналы. 1
Литература. 1
Т1. Основы теории радиотехнический сигналов. 1
Л1. Сигналы в радиотехнический информационных системах. 1
1. Введение. 1
2. Обобщенная структурная схема РТИС. 2
3. Классификация р/т сигналов. 2
Л2. Обобщенное представление сигналов. 2
1. Временное (динамическое) представление сигналов. 2
2. Геометрическое представление сигналов. 3
3. Спектральное представление сигналов. 3
Т2. Детерминированные сигналы. 4
Л3. Гармонический анализ периодических сигналов. 4
1. Тригонометрический ряд Фурье. 4
2. Комплексная форма ряда Фурье. 4
Т2.Л6. Сигналы с ограниченным спектром. 5
1. Теорема Котельникова (теорема отсчетов). 5
2. Оценка погрешности представления сигналов после усвоительности отсчетов. 5
3. Теорема остчетов в частотной области. 6
Т2.Л7. Цифровые сигналы. 6
1. Аналого-цифровое преобразование (АЦП) сигналов. 6
2. Характеристики цифровых сигналов. 6
Т3. Модулированные сигналы. 7
Л8. Сигналы с амплитудной модуляцией. 7
1. классификация видов модуляции. 7
2. принцип амплитудной модуляции. 7
3. балансная и однополосная АМ. 7
4. энергетические характеристики сигналов. 7
Т3.Л9. Сигналы с угловой модуляцией (УМ). 8
1. Обобщенное представление сигналов с УМ. 8
2. Сигналы с частотной модуляцией (ЧМ). 8
3. Спектральные характеристики сигнала с ЧМ. 8
Т3.Л10. Сигналы дискретной модуляции. 9
1. Сигналы дискретной АМ. 9
2. Сигналы дискретной ЧМ. 9
3. Сигналы дискретной ФМ. 10
1. Баскаков С.И. РТ цепи и сигналы, М, ВШ, 2000.
2. Гонаровский И.С., Делин Н.П. РТ цепи и сигналы, Радио и связь, 1994.
3. РТ цепи и сигналы под редакцией Самойлова К.А., М радио и связь, 1982.
1. Введение.
2. Обобщенная структурная схема РТИС.
3. Классификация р/т сигналов.
[Л.1], стр.11-16.
[Л.2], стр.6-8.
[Л.3], стр.11-13.
Радиотехника – научно-техническая область, изучающая принципы формирования и методы практического применения электрических сигналов и электромагнитных волн радиодиапазона для передачи информации на большие расстояния.
Диапазоны:
- мириаметровые (100-10км, 3-30кГц) СДВ.
- километровые (10-1км, 30-300кГц) ДВ.
- гектометровые (1км-100м, 300-3000кГц) СВ – средние волны.
- декаметровые (100-10м, 3-30МГц) КВ.
- метровые (10-1м, 30-300МГц) УКВ.
- дециметровые (1м-10см, 300-3000МГц) УКВ.
- сантиметровые (10-1см, 3-30ГГц) УКВ.
- миллиметровые (1см-1мм, 30-300ГГц) УКВ.
- децимиллиметровые (1-0,1мм, 300-3000ГГц).
- оптические (менее 0,1мм, более 3000ГГц).
ИРСы – системы радиосвязи, телевидение (изображение), радиоуправления (сигналы управления на расстоянии), радиолокации (определение местоположения объекта), радионавигации, радиотелеметрии (данные с летательных аппаратов).
1895г. Попов – беспроводная связь.
Объект изучения – различные виды р/т сигналов и устройств их преобразования для передачи информации.
Методика изучения– математическое моделирование сигналов и устройств, аппаратурный метод.
Цель изучения – повышение эффективности РТИС, использующихся для передачи информации.
ЗАДАЧИ РТ:
1. изучение различных видов р/т сигналов, их свойств и характеристик для использования в различных РТИС.
2. изучение принципов и методов преобразования р/т сигналов для решения задач построения Ртсистем. Предмет теории РТ цепей.
Модуляция – перенос первичного сигнала из НЧ диапазона в диапазон радиоволн.
Рис.1.2.1
Сигнал – любая физическая изменяющаяся величина, отображающее передаваемое сообщение.
(0,Т) Если Т конечно, то сигнал ограничен во времени (и наоборот).
(
,Т) Если Т равно 
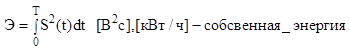
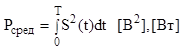
Сигналы – детерминированные (значение их в любое время можно предсказать) или случайные (параметры меняются случайным, непредсказуемым образом).
, S0- амплитуда сигнала.
Непрерывные и дискретные.
На практике нашли применение непрерывные, импульсные, цифровые сигналы.
По степени сложности:
- элементарные сигналы.
- сложные.
1. Временное (динамическое) представление сигналов.
2. Геометрическое представление сигналов.
3. Спектральное представление сигналов.
[Л.1], стр.16-34.
[Л.2], стр.9-13.
[Л.3], стр.30-39.
Предполагает описание сигнала в виде совокупности других более простых и изученных сигналов.
1. S(t)=sgn(t).
рис.2.1.1
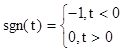(2.1)
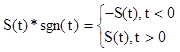
2.Ueg(t) – функция Хевисайда.
рис.2.1.2
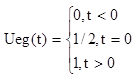(2.2)
– математическое выражение.
3. дельта-функция (
-функция).
Функция Дирака.
S0- амплитуда, 
- длительность; S0*=1
рис.2.1.3
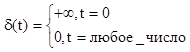(2.3)
Свойства
–функции.
- функция четная [S(t)=S0(-t)].
- 
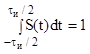- площадь.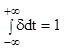 
-
фильтрующее свойство.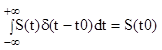 
(2.4)
4. rect[t/]
- единичный импульс.
Рис2.1.4
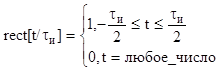(2.5)
(2.6)
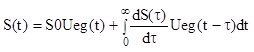(2.7)
рис.2.1.5
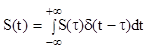
Рис.2.2.1
Совокупность точек, образованных концами векторов сигналов, образуют пространство векторов сигналов.
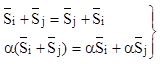(2.7) - пространство
сигнала линейное.
- норма вектора (длина).
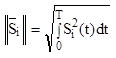(2.8) -
нормированное пространство.
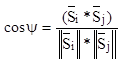(2.10)- расстояние между
векторами.
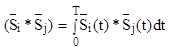- взаимная энергия.
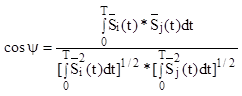(2.11)
Конечномерное (n-мерное) линейное нормированное метрическое пространство называется Евклидовым.
Бесконечное линейное нормированное метрическое пространство называется Гильбертовым.
Рис2.3.1
- ортогональные плоскости (0,Т),
если выполняется условие:
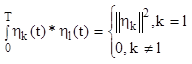(2.12)
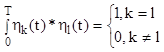(2.13) - ортонормированные
функции.
(2.14) - обобщенный ряд Фурье.
Умножим
на 
и найдем 
.
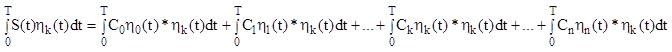
Еcли система ортонормированная.
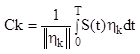(2.15)
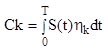(2.16)
Совокупность
коэффициентов Ск в разложенном уравнении (2.14) называется спектром сигнала в
координатном базисе {}.
Тогда функция (2.14) представляет собой обобщенное спектральное представление сигналов.
- гармонический базис.
, где T- длительность
сигнала.
Рис.2.3.2
Равенство Парсеваля.
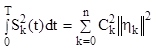(2.17)
.
.
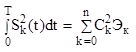Энергия сигнала=сумме энергий, его составляющих.
1. Тригонометрический ряд Фурье.
2. Комплексная форма ряда Фурье.
3. Распределение мощности в спектре периодического сигнала по частотам.
[Л1] стр. 38-43
[Л2] стр. 13-17
[Л3] стр. 41-49
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
