Формулы.
Эйлера.
Детерминированный сигнал – сигналы, значение которых знаем точно. Они не переносят информацию, используются для изучения характеристик реальных сигналов.
В РТ задачах в качестве базисных функций разложения в ряд Фурье используются тригонометрические (гармонические) функции.
Причины выбора:
- при прохождении через линейную цепь гармонические сигналы не меняют своей формы. Можно использовать принцип суперпозиции.
- гармонические сигналы просто формировать.
Рис.3.1.1
Разложение периодического сигнала в ряд Фурье возможно в том случае, если частота каждой гармонической составляющей кратна основной частоте () периодического сигнала.
- к-ая составляющая ГР.
Рис.3.1.2
Выводы по ф.(3.5):
1.
периодический сигнал состоит из постоянной составляющей и бесконечного числа
гармонических сигналов с амплитудами Ак и начальными фазами 
.
2.
совокупность Ак () называется амплитудным
(фазовым) спектром периодического сигнала.
3. спектр периодического сигнала называется линейчатым.
Рис.3.1.3.
Прибор спектр-анализатор.
Воспользуемся формулой Эйлера.
Тогда к-ая гармоника
(3.5) с учетом (3.8): (3.9) - комплексная форма ряда Фурье.
График спектра.
Рис.3.2.1
Рис.3.2.2
Область «+» частот является зеркалом области «-» частот.
Выводы.
1. Комплексная форма ряда Фурье предусматривает распространение, продолжение спектра в область «-» частот.
2. Спектр комплексной формы – линейчатый.
3. рис.3.2.3 – средняя мощность за период.
- мощность в физическом спектре.
- мощность в комплексном виде.
Условие излучения.
- расходящиеся сферические волны.
- вектор Пойтинга.
- сходящиеся сферические линии.
(при 
)
направлен вдоль радиуса от начала
координат.
Принцип взаимности.
Принцип Гюйгенса.
Теорема эквивалентности.
Теорема единственности.
1. теорема Котельникова (теорема отсчетов).
2. оценка погрешности представления сигналов после усвоительности отсчетов.
3. теорема остчетов в частотной области.
[Л1] стр. 119-126; [Л2] стр. 56-60; [Л3] стр. 66-74.
Гласит,
что любой сигнал, ограниченный по спектру в пределах 0-fверх. (0-
) может быть представлен
совокупностью своих мгновенных значений, взятых в момент времени tk, отстоящих друг от друга на интервал 
(
).
Математически
теорема записывается: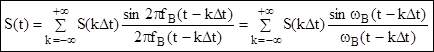 
(6.1)
Рис.2.6.1.1.
Процедура представления аналогового сигнала последовательностью мгновенных отсчетов, взятых в момент времени tk, называется дискретизацией.
Восстановить аналоговый сигнал можно используя идеальный фильтр низких частот.
Рис.2.6.1.2.
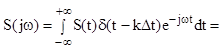(используя фильтрующее свойство
дельта-функции 
)=
.
Отклик фильтра:
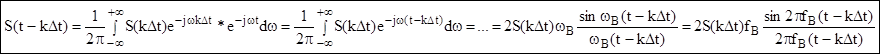(6.2)
Чем больше мы имеем откликов, тем лучше мы можем восстановить сигнал.
Рис.2.6.1.3.
Рис.2.6.1.4.
Если
сигнал имеет амплитудный спектр S(j
)
и энергетический спектр [S(j)]2,
то, начиная с некоторой частоты (если за пределами частот энергия сигнала
составляет менее 5%), можно применить теорему Котельникова:
; 
-
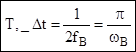база сигнала (6.3)
Тогда теорема записывается:
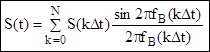- ряд Котельникова (6.4)
Таким образом, мы можем представить любой аналоговый сигнал.
Рис.2.6.2.1.
Энергия сигнала может быть определена как:
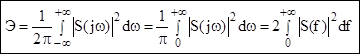(6.5)
- мера точности восстановления
сигнала (6.6)
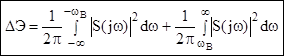(6.7)
На практике реализуют теорему Котельникова следующим образом:
1. Задаются требуемой точностью восстановления.
2. Исходя из выражения (6.6) определяем 
.
3. Зная в соответствии с
(6.7) можем найти 
.
4. Зная можем найти интервал дискретизации 
.
реально
интервал дискретизации выбирают из условия: 
.
Рис.2.6.3.1.
Если мы заменим:
, 
,
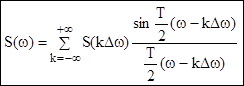- теорема Котельникова в частной
области (6.8)
1. Аналого-цифровое преобразование (АЦП) сигналов.
2. Характеристики цифровых сигналов.
[Л1] стр. 83-87; стр. 400-402; [Л2] стр. 306-308.
Для преобразования аналогового сигнала в цифровой необходимо осуществить операции дискретизации аналогового сигнала, его квантование по уровню и кодирование.
1. Дискретизация.
S(t)- аналоговый
сигнал, имеющий 
. Дискретизация
осуществляется в соответствии с теоремой Котельникова. Представляем этот сигнал
последовательностью импульсов 
.
; 
рис.2.7.1.1.
2. Квантование- округление значение
сигнала Sg(t) в моменты времени tk=k
t до ближайшего целого числа. Квантование осуществляется
квантователем, который имеет следующую амплитудную характеристику.
Рис.2.7.1.2.
Весь
диапазон значений сигнала Sg(t) разбивается на L уровней, каждый
из которых имеет 
– шаг квантования.
Если Sg(t)
находится в пределах 
(7.1), то 
(7.2)
рис.2.7.1.3.
Получаем квантованные значения дискретного сигнала.
- средняя ошибка квантования (шум
квантования) (7.3)
С.О.К. выражается в виде импульсов. Принципиально неустранима.
3. Кодирование. L обычно берут
равным 128
или
256.
(7.4)
- 
принимает
значения от 0 до (L-1).
L=10; 1986=A; n=4
A=1*103+9*102+8*101+6*100
n- количество разрядов данного числа.
Имеем
число, выраженное в разных системах L1 и L2. Соотносятся
эти системы так: n1logL1= n2logL2.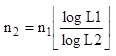 
(скобки –
округление до ближайшего целого числа).
Рис.2.7.1.4.
Рис.2.7.1.5.
Рис.2.7.1.6.
k()=const в пределах (0;fв).
Рис.2.7.2.1.
; 
.
Коэффициент сдвига m.
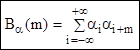- дискретная АКФ (7.5)
рис.2.7.2.2.
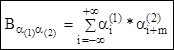(7.6)
1. классификация видов модуляции.
2. принцип амплитудной модуляции.
3. балансная и однополосная АМ.
4. энергетические характеристики сигналов.
[Л1] стр. 92-100; [Л2] стр. 73-79; [Л3] стр. 85-94.
Модуляция – преобразование сравнительно низких частотных сигналов в сигналы радиочастотного диапазона.
S(t), Uнес(t).
(8.1)
- правило преобразования сигнала S(t) в
сигнал U(t).
Оно устанавливает вид несущего колебания; параметр несущего колебания, который изменяется в зависимости от S(t); вид самого колебания.
Виды модуляции.
А). По виду управляющего сигнала: 1. непрерывная; 2. дискретная (манипуляция);
Б). По виду несущего колебания: 1. гармоническая; 2. импульсная; 3. псевдослучайная.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.