Электротехника \ Радиотехнические цепи и сигналы

Краткие сведения для выполнения лабораторных работ по дисциплине "Радиотехнические цепи и сигналы", страница 3

В). по виду управляемого параметра несущего колебания: 1. амплитудная; 2. частотная (широтная); 3. фазовая; 4. временная (по форме).

На практике чаще всего используется гармоническое несущее колебание.

2. принцип амплитудной модуляции.

Сигналы амплитудной модуляции, это сигналы, у которых амплитуда гармонического несущего колебания изменяется в соответствии с управляющим сигналом S(t).

В общем виде сигнал АМ записывается:

, где кАМ- коэффициент АМ.

Рис.3.8.2.1.

;       (8.3)

Коэффициент АМ определяет глубину модуляции.

, 

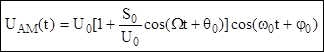      (8.4)

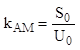(для данного случая).

Рис.3.8.2.2.

    (8.5)

Это выражение дает информацию о спектре сигнала однотональной модуляции.

Рис.3.8.2.3.

Выводы: спектр однотонального модулированного колебания содержит составляющую несущего колебания на частоте  и две боковые составляющие, расположенные на частотах , .

,  .

Рис.3.8.2.4.

Сигналы произвольной формы.

Рис.3.8.2.5.

Спектр АМ колебания с управляющим сигналом произвольной формы содержит составляющую несущего колебания и две боковые полосы. Верхняя боковая полоса соответствует спектру исходного управляющего сигнала S(t), но сдвинутого по оси  на величину . Нижняя боковая полоса является зеркальным отображением верхней боковой полосы.

3. балансная и однополосная АМ.

Балансная модуляция – это есть амплитудная модуляция с подавленным несущим колебанием в спектре.

     (8.6)

рис.3.8.3.1.

Однополосная модуляция – модуляция с подавленным несущим колебанием и одной их боковых полос.

       (8.7)

рис.3.8.3.2.

Получается при помощи двух балансных модуляторов.

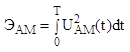
4. энергетические характеристики сигналов.

Если подставить (8.5), то получим:

   (8.8)

Энергия распространяется между двумя колебаниями

        (8.9)

ОАМ- сложность аппаратурной реализации.

Т3.Л9. Сигналы с угловой модуляцией (УМ).

1. обобщенное представление сигналов с УМ.

2. сигналы с частотной модуляцией (ЧМ).

3. Спектральные характеристики сигнала с ЧМ.

[Л1] стр. 100-107; [Л2] стр. 79-90; [Л3] стр. 94-101.

1. Обобщенное представление сигналов с УМ.

(9.1)

- текущая фаза сигнала             (9.2)

Основная информация заложена в управляющем сигнале; условная – частотная + фазовая модуляции.

Сигналы с УМ характеризуются тем, что в соответствии с управляющим сигналом S(t) изменяется полная фаза несущего колебания.

Сигналы УМ делятся на два вида:

1. сигналы ЧМ. Характеризуются тем, что мгновенная частота несущего колебания изменяется по закону  (9.3), где – девиация частоты (показывает максимальное отклонение мгновенной частоты от частоты несущего колебания ). Различают девиацию вверх () и вниз ().  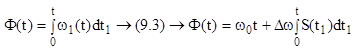. При ЧМ полная фаза модулированного сигнала изменяется по закону интегрирования от управляющего сигнала.

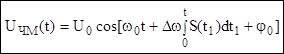 (9.5) – обобщенное выражение для сигнала с ЧМ.

2. сигналы ФМ. Характеризуется изменением начальной фазы сигнала, а полная фаза:  (9.6), где – девиация фазы. (9.7) – мгновенная частота меняется по закону производной управляющего сигнала S(t).

 (9.8) – обобщенное выражение сигнала с фазовой модуляцией.

2. Сигналы с частотной модуляцией (ЧМ).

(с единичной амплитудой).

В соответствии с (9.5):

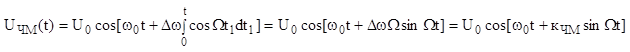  (9.9), где – индекс (коэффициент ЧМ), показывающий, какое количество девиации частоты приходится на 1 модулируемого сигнала).

         (9.11)

Однотональная  ЧМ.

Случаи малых индексов:

1. кЧМ<<1,

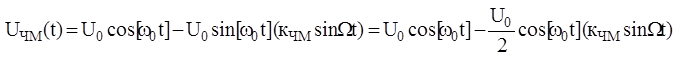              (9.12)

рис.3.9.2.1.

Вывод: при малых значениях индекса ЧМ (кЧМ), спектр однотонального модулированного ЧМ сигнала содержит составляющую несущего колебания и две боковые составляющие на частотах (), (), имеющих одинаковые амплитуды, но противоположные начальные фазы.

Девиация частоты: f=75кГц; f=15кГц; кЧМ=5.

3. Спектральные характеристики сигнала с ЧМ.

(9.11) – общее выражение.

, где – функция Бесселя первого рода i–го порядка.

{Ai=UoYi(кЧМ)}

              (9.13)

- спектральная составляющая несущей частоты.

Теоретически, спектр бесконечен.

Амплитуды этих составляющих зависят от кЧМ.

Рис.3.9.3.1.

При кЧМ +1 ;

При кЧМ>>1 ;

Ширина спектра: .

Выводы:

1. Спектр частотно модулируемого сигнала при произвольных значениях кЧМ содержит составляющую несущего колебания и две боковые полосы.

2. Боковые полосы содержат теоретически бесконечное число гармонических составляющих, амплитуды которых определяются значением кЧМ.

3. Начальные фазы составляющих верхней боковой полосы одинаковы и равны «0». Начальные фазы составляющих нижней боковой полосы с несимметричными индексами равны «», а с четными – «0».

4. Практическая ширина спектра однотипного сигнала с ЧМ равна удвоенной девиации частоты.

Т3.Л10. Сигналы дискретной модуляции.

1. Сигналы дискретной АМ.

2. Сигналы дискретной ЧМ.

3. Сигналы дискретной ФМ.

[Л1] стр. 97-100; [Л] Д.Хловский: «Теория передачи сигнала» изд. Связь, 1973. стр. 93-94.

1. Сигналы дискретной АМ.

АТ – амплитудная телеграфия (ДАМ).

ЧМ – частотная телеграфия (ДАМ).

ФМ – фазовая телеграфия (ДФМ).

Рис.3.10.1.1.

             (10.1)

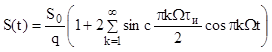
(в данном случае)

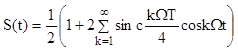 в 10.1

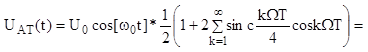
 (10.2)

Колебание дискретной АМ.

Рис.3.10.1.2.

Выводы:

1. Спектр сигнала ДАМ содержит составляющую несущего колебания и две боковые полосы зеркально расположенных относительно частоты несущего колебания.

2. Огибающая каждой из боковых полос совпадает с огибающей спектра модулирующего сигнала (спектра периодической последовательности импульсов со скважностью q=2).

2. Сигналы дискретной ЧМ.

Рис.3.10.2.1.

;

;

;

;

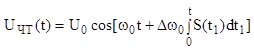
где ;

-; -, где S1(t)–отрицательные импульсы; S2(t)-только положительные импульсы.

              (10.3)

              (10.4)

    (10.5)

Рис.3.10.2.2.

Рис.3.10.2.3.

Если              (10.6).

Выводы:

1. Спектр сигналов дискретной ЧМ содержит 2 спектра, сосредоточенных вокруг частот  и , где ;  .

2. Каждый из спектров содержит составляющую на частотах  и  и две боковые полосы, зеркально отображающие друг друга относительно частоты  и .

3. Огибающая спектра повторяет форму огибающей спектра управляющего сигнала S(t) (периодической последовательности прямоугольных импульсов).

3. Сигналы дискретной ФМ.

Рис.3.10.3.1.

 если , то

 где

l=0 или l=1

;  ; 

Представим:

Рис.3.10.3.2.

Рис.3.10.3.3.

Выводы:

1. Спектр сигнала ДФМ не содержит составляющую несущего колебания, а содержит две боковые полосы, зеркально расположенные относительно частоты несущего колебания ().

2. Амплитуды спектральных составляющих боковых полос сигналов ФМ вдвое больше амплитуд соответствующих составляющих спектра сигнала амплитудной модуляции.

Скачать файл