Основные распределения, используемые в теории надежности

Глава 1.3

ОСНОВНЫЕ РАСПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ В ТЕОРИИ НАДЕЖНОСТИ

До рассмотрения распределений, используемых в теории надежности ознакомимся с очень популярной кривой, ставшей уже классической, которая отображает поведение  интенсивности отказов в зависимости от времени (наработки). Идеализированный вид кривой представлен на рис. 1.3.1.

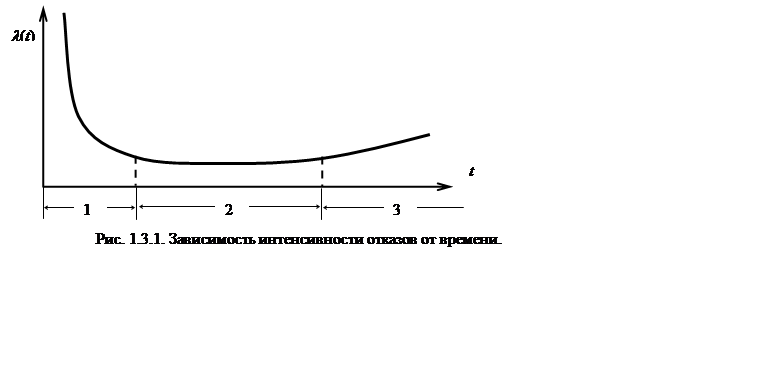
Такого вида кривые были получены в результате статистической обработки данных об отказах и наработке при испытаниях и эксплуатации многих технических (и не только технических) объектов. Как правило на такой кривой можно выделить три участка.

Первый участок называют этапом приработки. Для этого этапа характерна повышенная интенсивность отказов, которая снижается со временем. Это объясняется следующими причинами. В любом новом объекте имеются материалы и элементы со скрытыми дефектами, а также всевозможные проектные, конструкторские и производственные ошибки, которые в большей степени и проявляются на начальном этапе жизни объекта, приводя к повышению интенсивности отказов. По мере их устранения снижается количество отказов, что, в конечном итоге, приводит к уменьшению интенсивности отказов.

Следует отметить, что срок гарантии, устанавливаемый на различные объекты, это часть интервала приработки, причем, как правило, незначительная.

Второй участок называется этапом нормальной работы. Здесь интенсивность отказов обычно имеет приблизительно (практически) постоянный характер. Этот этап, по существу и определяет фактический ресурс объекта.

Третий участок называется этапом старения. На этом участке происходит возрастание интенсивности отказов в результате необратимых физико-химических процессов в материалах, которые приводят к ухудшению качества элементов и объекта в целом.

В соответствии с убыванием или возрастанием интенсивности отказов в теории надежности рассматриваются «молодеющие» или «стареющие» объекты и соответствующие им распределения, описывающие распределение времени безотказной работы объектов.

«Молодеющий» -	объект (распределение), у которого интенсивность отказов монотонно убывает, т.е. при  справедливо неравенство .
«Стареющий» -	объект (распределение), у которого интенсивность отказов монотонно возрастает, т.е. при  справедливо неравенство .
«Вневозрастной» -	объект (распределение), у которого интенсивность отказов постоянна, т.е.  при .

1.3.1. Непрерывные распределения.

В данном разделе приводятся наиболее часто применяемые в теории надежности распределения непрерывных случайных величин, для описания характеристик безотказности и ремонтопригодности. Отличительной особенностью этих случайных величин является то, что они не могут быть отрицательными. Следовательно, для функций распределения , используемых в теории надежности справедливо равенство .

Для адекватного применения того или иного распределения при описания характеристик конкретного объекта требуется добиться максимального соответствия свойств объекта и распределения.

1.3.1.1. Экспоненциальное распределение.

Вероятность безотказной работы в этом случае имеет вид при

,

(1.3.1)

где l - параметр распределения.

Функция распределения и плотность распределения времени безотказной работы соответственно равны

,	(1.3.2)
.	(1.3.3)

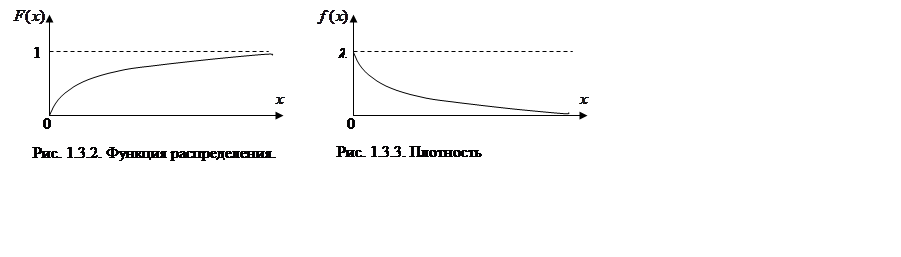
Графики функции и плотности распределения для экспоненциального распределения представлены на рис. 1.3.2 и 1.3.3.

По формуле (2.1.7) для интенсивности отказов имеем

.

(1.3.4)

Таким образом, параметр l в (1.3.1) – это интенсивность отказов, которая для экспоненциального распределения является постоянной величиной при , т.е. экспоненциальное распределение является «вневозрастным» распределением.

Средняя наработка до отказа по (2.1.14) равна

.

(1.3.5)

То есть, для экспоненциального распределения средняя наработка до отказа обратно пропорциональна интенсивности отказов и, поэтому, часто вместо (1.3.1.) пишут

.

(1.3.6)

Определим значение дисперсии в случае экспоненциального распределения. Так как 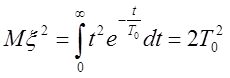, то с учетом равенств (2.1.15) и (1.3.16), получим . То есть, для экспоненциального распределения дисперсия наработки до отказа равна квадрату математического ожидания наработка до отказа.

Экспоненциальное распределение обладает свойством, которое называют свойством отсутствия последействия. При рассмотрении безотказности объекта его можно сформулировать таким образом: если в некоторый момент времени объект работоспособен, то время, которое он проработает безотказно с этого момента, не зависит от того, сколько он работал до этого момента. Это означает, что в случае экспоненциального распределения условная вероятность безотказной работы объекта на интервале (t, t+t) при условии, что объект не отказал на интервале (0, t), не зависит от времени предшествующей работы t, а зависит только от длительности рассматриваемого интервала t. Условная вероятность этого события обозначается, как  и представляет собой распределение остаточного времени «жизни» объекта x_t, определяемого равенством

.

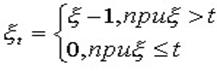Экспоненциальное распределение в силу свойства отсутствия последействия противоречит естественным физическим представлениям. Это фактически означает отсутствие старения, что не соответствует реальным техническим объектам в процессе их эксплуатации, особенно на больших интервалах времени.

Экспоненциальное распределение будет не справедливым и для времени восстановления. Продолжительность работы по каждому восстановлению объекта ограничена и выражается числом часов. Поэтому время, которое осталось затратить на окончание восстановительных работ, конечно, будет зависеть от уже затраченного времени восстановления.

Таким образом, надо иметь веские основания для применения экспоненциального распределения, впрочем как и для любого другого.

Тем не менее, экспоненциальное распределение весьма популярно в теории надежности по следующим причинам.

Во первых, экспоненциальное распределение очень простое, зависит от одного параметра l .Это совместно со свойством отсутствия последействия позволяет решение многих задач теории надежности представить в явном аналитическом виде.

Во вторых, практически и теоретически доказано, что время безотказной работы сложных высоконадежных восстанавливаемых систем при определенных условиях хорошо описывается экспоненциальным распределением. Например, одним из таких условий является рассмотрение интервалов работы, на которых влиянием «старения» материалов (элементов) можно пренебречь.