Приведенные в главе 1 определения основных понятий и терминов, применяемых в теории надежности, имеют описательный характер и не могут быть непосредственно использованы при разработке и построении математических моделей теории надежности, если не ввести количественных характеристик свойств объекта, которые описываются показателей надежности.
Показатель надежности - |
количественная характеристика одного или нескольких свойств (безотказность, ремонтопригодность, долговечность и сохраняемость), составляющих надежность объекта. |
Принципиально важным в теории надежности является наличие и проявление свойств во времени. Поэтому и рассматривается время от момента проявления свойства, до момента окончания его реализации. Последнее происходит в результате некоторого случайного события (например отказ, завершения ремонта), которое могло произойти в любой момент времени. Интервалы времени от момента начала проявления свойства до момента окончания его реализации рассматриваются как случайные величины и обычно обозначаются греческими буквами x (кси), h (эта) и т.д. С этими случайными величинами не следует путать рассматриваемый фиксированный интервал времени, длительность которого обозначают буквой t . Это позволяет рассматривать различные случайные события, например {x > t}, {x < t}, что означает, отказал или не отказал объект на интервале (0, t). При этом величину t выбирает исследователь или она устанавливается в нормативных документах, а значение x определяет «Его величество случай».
В теории надежности используются как непрерывные (наработка на отказ), так и дискретные(число отказов) случайные величины.
Время или наработка до отказа объекта, (интервал времени от начала его работы (от нуля) до момента появления первого отказа), можно рассматривать как непрерывную случайную величину x.
Введем основные показатели безотказности.
Вероятность безотказной работы - |
вероятность того, что в пределах заданной наработки на отказ объекта не происходит. Это основной показатель безотказной работы. |
Определим этот показатель на фиксированном интервале (0, t) и обозначим его ![]() .
.
|
|
(1.2.1) |
Р - здесь и далее обозначает функцию вероятности.
Таким образом, ![]() - это вероятность того, что отказ на
интервале (0, t) не произошел, см. рис
1.1.
- это вероятность того, что отказ на
интервале (0, t) не произошел, см. рис
1.1.
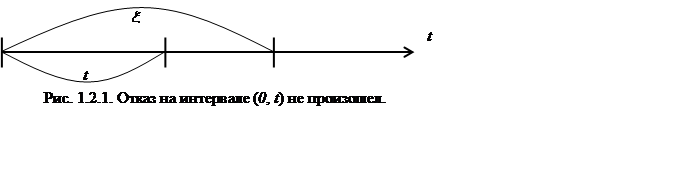
Здесь речь идет о новом
объекте, который начал работать при t=0. Если он
не отказал до момента t, т.е. осуществилось
событие {x > t}, то говорят, что к моменту
времени t имеет возраст t. При необходимости определения вероятности того, что
объект, имеющий возраст t, проработает
безотказно еще не менее времени t (рис.
1.2), необходимо использовать условную вероятность ![]() , которая согласно теореме
перемножения вероятностей равна
, которая согласно теореме
перемножения вероятностей равна
|
|
(1.2.2) |
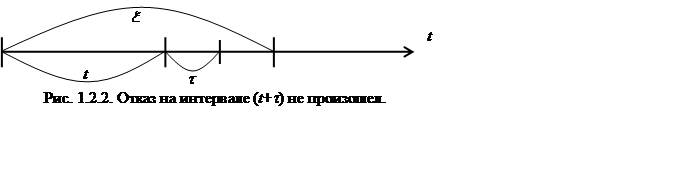
Вероятность ![]() часто называют функцией надежности.
В теории вероятностей обычно рассматривают функцию распределения. Обозначив ее
через
часто называют функцией надежности.
В теории вероятностей обычно рассматривают функцию распределения. Обозначив ее
через ![]() по определению будем иметь
по определению будем иметь ![]() , откуда следует, что
, откуда следует, что
|
|
(1.2.3) |
Необходимо отметить, что
вероятность отказа объекта на бесконечно малом интервале времени {t, t+dt}
(или в момент времени t) согласно теории
вероятностей должна быть записана в виде ![]() или
или
![]() .
.
Если x непрерывная случайная величина и учитывая свойства функции
распределения (неубывающая функция от нуля F(0)
= 0 до единицы ![]() , то получим, что функция
, то получим, что функция ![]() не возрастает от единицы до нуля,
при этом
не возрастает от единицы до нуля,
при этом
|
|
(1.2.4) |
Все остальные показатели безотказности выражаются
через вероятность безотказной работы ![]() .
.
Интенсивность отказов - |
плотность условной вероятности возникновения отказа объекта, при условии, что до рассматриваемого момента времени отказ не возник. |
Интенсивность отказов обозначается как l(t) и определяется по формуле
|
|
(1.2.5) |
Так как согласно (1.2.3.)
|
|
(1.2.6) |
где ![]() обозначает плотность
распределения случайной величины x,
то (1.2.5) можно представить в виде
обозначает плотность
распределения случайной величины x,
то (1.2.5) можно представить в виде
|
|
(1.2.7) |
Для пояснения вероятностного смысла интенсивности отказов возьмем два интервала времени (0, t) и (0, t1), причем t1 > t. Рассмотрим 3 события А, В и С, где
Отсюда следует С = А Ç В и Р{С} = P{А Ç В}. По теореме умножения вероятностей имеем
Р{С} = P{А Ç В} = P{B/А }P{A},
где через P{B/А } обозначена условная вероятность того, что объект не отказал на интервале (t, t1), при условии, что он не отказал на интервале (0, t). Обозначим
R(t, t1) = P{B/А }.
Тогда
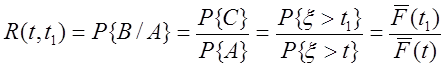 .
.
Если условную вероятность отказа объекта на интервале (t, t1) при условии, что он не отказал на интервале (0, t). Обозначить через Q(t, t1), то получим
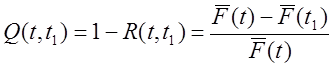 .
.
Пусть t1 = t + Dt, где Dt – бесконечно малая величина. В этом случае
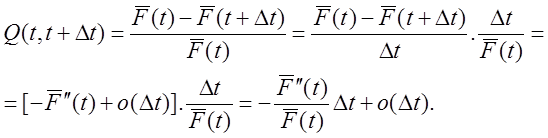
Учитывая (1.2.5) получим
|
|
(1.2.8) |
Так как безусловная и условная вероятность появления события на интервале
(t, t + Dt) выражается как произведение соответствующей плотности вероятности и интервала Dt, то из (1.2.8) непосредственно следует смысл интенсивности отказов.
Интенсивность отказов статистически определяется следующим образом. Из (1.2.5) имеем
|
|
(1.2.9) |
Предположим, что для определения значения l(t) в момент t были проведены испытания на надежность N объектов (необходимо, чтобы это число было достаточно большим) в течение времени t + Dt. Число объектов не отказавших на интервале (0, t) обозначим n(t), а число отказавших объектов на интервале (t + Dt) как Dn = n(t) - n(t + Dt).
На основе статистической оценки частоты возникновения события (вероятности) можно записать
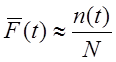 .
.
Тогда, учитывая (1.2.3.8), получаем
|
|
(1.2.6) |
Таким образом, статистическая интенсивность отказов в момент времени t приближенно равна числу отказавших объектов в единицу времени на интервале (t,t + Dt) деленному на число объектов, не отказавших к моменту времениt.
Выражения для определения вероятности безотказной работы через интенсивность отказов можно получить путем решения дифференциального уравнения (1.2.5) при начальном условии
|
|
(1.2.11) |
Запишем (1.2.5) в виде
|
|
Отсюда получаем
|
|
Учитывая (1.2.1), находим
|
|
(1.2.12) |
То есть, если известна интенсивность отказов на интервале (0,T), то можно вычислить вероятность безотказной работы объекта на том же интервале времени.
Часто этот показатель называют средним временем безотказной работы и обозначают Т0.
Средняя наработка до отказа - |
Это математическое ожидание наработки объекта до первого отказа. |
|
|
(1.2.13) |
где ![]() - плотность распределения
случайного времени безотказной работы x
.
- плотность распределения
случайного времени безотказной работы x
.
Иная запись (1.2.13) получается с учетом (1.2.6) и интегрированием по частям
|
|
(1.2.14) |
Следовательно, средняя наработка до отказа равна площади под кривой вероятности безотказной работы.
Помимо приведенных выше показателей безотказности часто рассматривают дисперсию наработки на отказ (s2 ).
|
|
(1.2.15) |
Учитывая (1.2.13), получим
|
|
где
|
|
Следует помнить, что приведенные показатели безотказности относятся к новым работоспособным объектам, которые включаются в работу в нулевой момент времени.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.