Другие предметы \ Теория надежности сложных систем

Основные распределения, используемые в теории надежности, страница 2

В третьих, использование экспоненциального распределения даже в тех случаях, когда оно не справедливо, позволяет при определенных условиях получать для показателей надежности заниженные результаты, т.е. оценки снизу. А это на практике часто устраивает многих.

Одной из важнейших таких оценок является утверждение [15].

УТВЕРЖДЕНИЕ. Если для расчета вероятности безотказной работы «стареющего» объекта использовать экспоненциальное распределение, в которое подставлена истинная средняя наработка до отказа , то справедлива оценка

(1.3.12)

1.3.1.2. Распределение Вебулла – Гнеденко.

Распределение Вебулла – Гнеденко определяется равенством

(1.3.22)

Функция распределения равна

(1.3.23)

Плотность распределения

(1.3.24)

В этих формулах l - параметр масштаба, a - параметр формы.

На рис. 1.3.4 и 1.3.5 представлен общий вид кривых вероятности безотказной работы и плотности распределения для распределения Вейбулла – Гнеденко при l = 1.

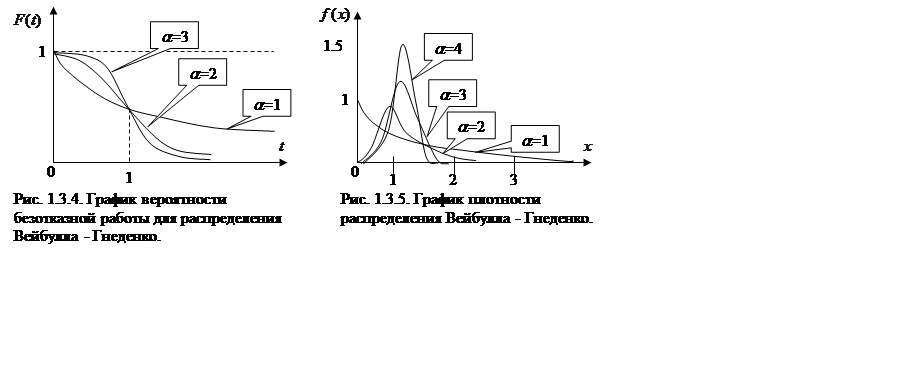
Определим среднюю наработку да отказа

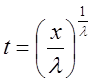Сделаем замену . Отсюда и 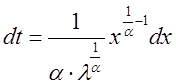. Поэтому

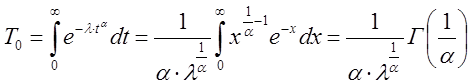, где 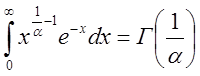- гамма функция.

Учитывая известное свойство этой специальной функции , получаем

1.3.25

Дисперсия случайной величины, распределенной по закону Вейбулла – Гнеденко, имеет вид

1.3.26

Интенсивность отказов

1.3.27

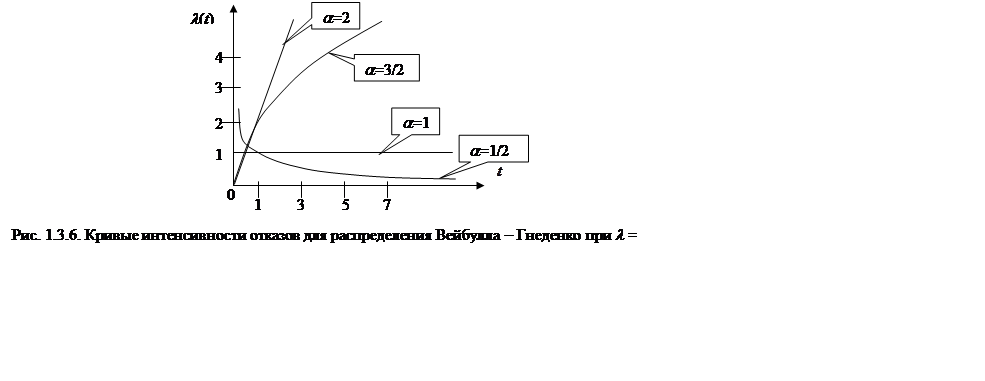
Характер поведения функции интенсивности отказов зависит от значений параметра a (см. рис. 1.3.6).

При распределения Вейбулла – Гнеденко является «молодеющим» распределением , при - «стареющим», а при совпадает с экспоненциальным распределением. С помощью этого распределения может быть представлена наработка до отказа объектов, которые имеют скрытые дефекты, но которые относительно долго не стареют. Так же этот закон может быть справедлив для объектов, у которых отсутствуют скрытые дефекты, но которые относительно быстро стареют. Например, известно, что законом Вейбулла – Гнеденко хорошо описывается распределение наработки до отказа ряда электровакуумных ламп, некоторых типов полупроводниковых приборов, подшипников качения.

1.3.1.3. Нормальное и усеченное нормальное распределение.

Известно, что плотность и функция нормального распределения существуют на интервале , и в общем случае соответственно имеют вид

,	1.3.28
.	1.3.29

Часто в приложениях теории вероятности применяется так называемое стандартное нормальное распределение, где среднее значение (a) равно нулю, а дисперсия (s) равна единице. Это легко получить, применяя операции центрирования и нормирования. Вид кривых плотности и закона стандартного нормального распределения приведен на рис.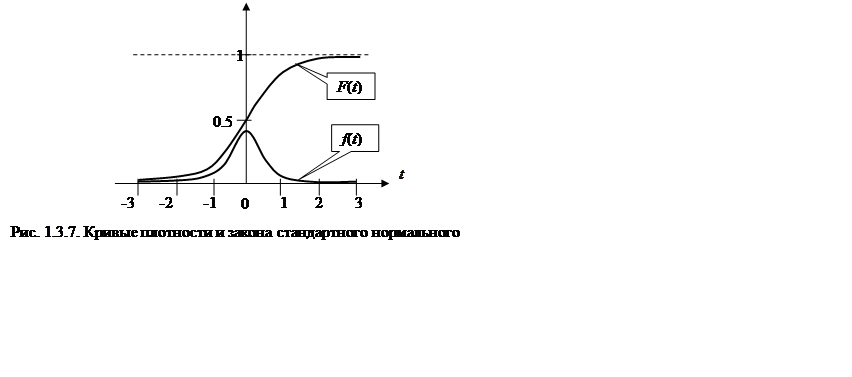
1.3.7.

Нормального распределения существуют на интервале , но время, основная характеристика параметров надежности, не может быть отрицательным. Поэтому в теории надежности использовать нормальное распределение, как распределение наработки до отказа объекта, возможно, строго говоря, только при рассмотрении усеченного нормального распределения на интервале , плотность вероятности которого задается функцией

1.3.28

где определяется при формулой (1.3.28). Константа находится из условия нормировки 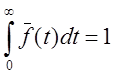, то есть

1.3.43

Отсюда можно получить, что 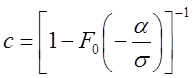. (Важно как в таблице задана стандартная функция )

Усеченное нормальное распределение на практике в представленном виде используется относительно редко.

Однако, если выполняется условие

1.3.46

которое часто справедливо, то без больших погрешностей можно применять не усеченный нормальный закон в виде (1.3.28) и (1.3.29). Это условие означает, рассеяние случайных величин, характеризуемое средним квадратичным отклонением , более чем в три раза меньше математического ожидания. В этом случае площадь под кривой плотности распределения при весьма мала и ею можно пренебречь. Тогда , средняя наработка до отказа , а дисперсия наработки до отказа равна .

Определим остальные важнейшие показатели безотказности для усеченного нормального распределения.

Вероятность безотказной работы равна

1.3.47

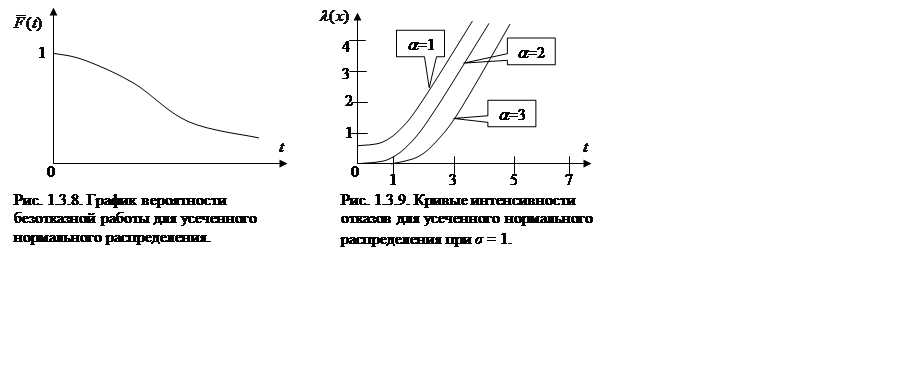
Вид этой функции представлен на рис. 1.3.8.

Интенсивность отказов равна

1.3.48

Графики интенсивности отказов для усеченного нрмального распределения приведены на рис 1.3.9.

Нормальному закону хорошо соответствует распределение наработки до отказа тех объектов, у которых процессы изнашивания или старения протекают не очень быстро. Это относится к ресурсу ряда электровакуумных и полупроводниковых приборов. В силу симметричности плотности нормального распределения относительно средней наработки до отказа , 50% процентов отказов происходит до этого момента и 50% отказов – после.

Для использования таблиц значений стандартной функции нормального распределения для оценки вероятности отказа объекта на интервале (0, t), t ≥ 0 используют соотношения 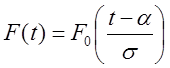, а определения плотности этого распределения формулой .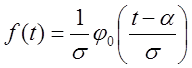

Вероятность безотказной работы на интервале (0, t), t ≥ 0, определяется по формуле 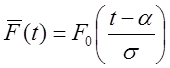, т. к. .

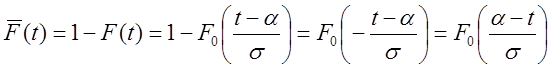Учитывая полученные выражения и (2.1.7) определим интенсивность отказов для использования таблиц стандартного нормального распределения.

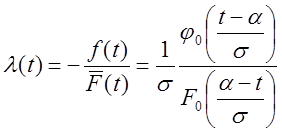Табулированные значения этой функции приведены в табл. П.2.11. [1].

1.3.1.4. Гамма - распределение.

Плотность гамма - распределения имеет вид при

, ,		1.3.51
где	.	1.3.52

Это распределение зависит от двух положительных параметров λ – параметра масштаба и α – параметра формы. График плотности гамма – распределения приведен на рис.1.3.10.

Вероятность безотказной работы равна