Основные распределения, используемые в теории надежности, страница 3

Из этого соотношения следует, что при функция  возрастает, то есть интенсивность отказов убывает и, следовательно на этом интервале гамма – распределение является «молодеющим» распределением.

При  функция  убывает, то есть интенсивность отказов возрастает и, следовательно при  гамма – распределение является «стареющим» распределением.

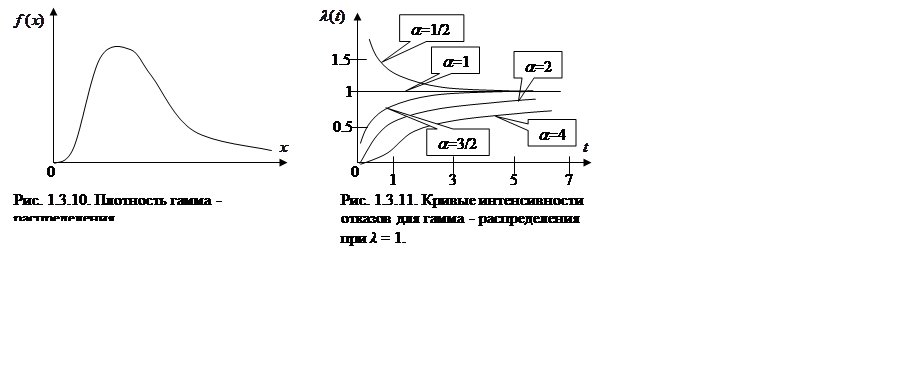
Характер поведения интенсивности отказов для некоторых значений представлен на рис. 1.3.11.

Гамма – распределение используется при рассмотрении долговечности (ресурса) некоторых объектов. При этом часто используется при целых значения . Доказано, что гамма – распределение с параметрами  и m является распределением суммы m независимых случайных величин, имеющих одинаковое экспоненциальное распределение с параметром .

1.3.1.5. Смесь непрерывных распределений.

Не всегда наработку до отказа можно описать приведенными или иными распределениями в чистом виде. В этом случае могут быть использованы так называемые смеси распределений.

Пусть имеется n случайных величин ; k – я случайная величина берется с вероятностью , где 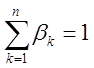, причем известны вероятности .

Тогда смесью распределений случайных величин  называется вероятность

.

1.3.62

Рассмотрим пример. Предположим, что некоторый элемент изготавливается на n разных заводах. Известно, что вероятность безотказной работы элемента, изготовленного k – тым заводом, экспоненциальна с параметром , то есть .

Элементы с разных заводов поступают на склад, где случайным образом перемешиваются. Долю продукции на складе, поступившую с k – того завода, обозначим . Тогда вероятность безотказной работы элемента, взятого на складе, определяется по (1.3.62)

1.3.2. Дискретные распределения.

В теории надежности для описания характеристик безотказности и ремонтопригодности так же используются распределения дискретных случайных величин. Дискретная случайная величина задается ее значениями (x₀, x₁, x₂,…..) и вероятностями этих значений ( при k = 0, 1, 2,…..). Вероятности  удовлетворяют условиям нормировки

.

1.3.64

Наиболее популярными дискретными распределениями в теории надежности являются распределение Пуассона, биномиальное распределение, отрицательное биномиальное распределение и геометрическое распределение. Приведем основные соотношения и характеристики этих распределений [1].

1.3.2.1. Распределение Пуассона

Случайная величина , распределенная по закону Пуассона, принимает целочисленные значения  с вероятностью

,

1.3.65

где  - параметр распределения.

Математическое ожидание пуассоновского распределения равно параметру распределения .

.

1.3.66

Дисперсия пуассоновского распределения так же равна параметру распределения .

.

1.3.71

В теории надежности распределение Пуассона применяется (для описания) как распределение числа отказов сложных восстанавливаемых систем на заданном интервале времени t. Соответствующая случайная величина, которая определяет число отказов системы на интервале , уже будет зависеть от времени. Тогда говорят о случайном пуассоновском процесс, который обозначают как  ().

При фиксированном времени t функция  будет случайной величиной, распределенной по закону Пуассона с параметром . Здесь 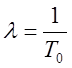 является интенсивностью отказов системы, а , соответственно, средней наработкой между двумя соседними отказами системы. Тогда закон распределения Пуассона можно записать

,

1.3.75

причем  это среднее число отказов системы на интервале . Тогда математическое ожидание и дисперсия пуассоновского распределения равны отказов системы это среднее число отказов системы на интервале .

.

1.3.71

1.3.2.2. Биномиальное распределение

Случайная величина , принимающая целочисленные значения 0, 1, 2,…..n, будет иметь биномиальное распределение если

,

1.3.77

где

1.3.78

число сочетаний из n по k (биномиальные коэффициенты), ; k = 0, 1, 2,…..n, (n и p – параметры биномиального распределения).

Вероятности  удовлетворяют условию нормировки, т.е.

.

1.3.79

Математическое ожидание биномиально распределенной случайной величины определяется параметрами распределения n и p.

.

1.3.71

Дисперсия биномиально распределенной случайной величины также выражается через параметры n и p биномиального распределения.

.

1.3.71

Биномиальное распределение, как известно из теории вероятностей, имеет место в схеме испытаний Бернулли. В теории надежности биномиальному распределению подчиняется, например, число отказавших элементов в схеме, состоящей из nосновных и m резервных элементов при нагруженном резерве.

При больших значения n (n > 100) и не очень малых значениях p (npq >20) биномиальное распределение хорошо аппроксимируется нормальным распределением.

1.3.2.3. Отрицательное биномиальное распределение

Случайная величина , принимающая целочисленные значения r, r+ 1,….. имеет отрицательное биномиальное распределение, если

,

1.3.85

число сочетаний из n по k (биномиальные коэффициенты), ; s =  r, r+ 1,….. Вероятности  удовлетворяют условию нормировки, т.е.

.

1.3.86

Отрицательное биномиальное распределение так же имеет место в схеме испытаний Бернулли. Но в отличии от биномиального распределения, когда число испытаний задано, здесь число испытаний является случайной величиной.

Математическое ожидание и дисперсия случайной величины ξ , распределенной по отрицательному биномиальному распределению соответственно определяются параметрами n и r.

,	1.3.87
.	1.3.88

В теории надежности вид отрицательного биномиального распределения имеет вероятность подключения фиксированного числа резервных элементов при нагруженном резерве.

1.3.2.4. Геометрическое распределение.

Случайная величина  имеет геометрическое распределение, если она принимает целочисленные значения 1, 2,…..n,…. с вероятностями

,

1.3.89

где q=1-p, k=1, 2,…..n,…

Вероятности (последовательность) удовлетворяют условию нормировки

.

1.3.90

Математическое ожидание и дисперсия случайной величины ξ , распределенной по геометрическому распределению соответственно определяются как

,	1.3.92
.	1.3.95

Геометрическое распределение используется в теории надежности, напрмер, там, где наработка отсчитывается дискретными единицами (числом включений, коммутаций, пусков и т.п.).