МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ИНСТИУТ ТЕХНИКИ ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
КАФЕДРА ОБЩЕЙ ФИЗИКИ И ЭЛЕКТРОТЕХНИКИ
ЛАБОРАТОРНАЯ РАБОТА №2
ПО КУРСУ «ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ»
ПО ТЕМЕ «ИССЛЕДОВАНИЕ РЕЗОНАНСА НАПРЯЖЕНИЙ»
Выполнили
ст.гр.УИТ-31 В
Кардецкая О.
Узюкова О.
Стройкова Т.
Гросс С.
Катышев А.
Малофеева Т.
Проверил
Зайцев А.В._______
<___>________2003г.
Балаково 2003
ИССЛЕДОВАНИЕ РЕЗОНАНСА НАПРЯЖЕНИЙ
Цель работы: экспериментальное исследование цепи синусоидального тока с последовательным соединением элементов; определение условий, при которых наступает резонанс; определение параметров схемы резонансным методом.
Основные понятия: Рассмотрим последовательное соединение резистивного, индуктивного и емкостного элементов (рис.1). Такую цепь называют последовательным контуром или R, L, C цепью.
Рис.1 Рис.2 Рис.3
Полное комплексное сопротивление Z такой цепи определяется по формуле:
Z = R + jωL + 1/jωC = R + j(XL + XC) = R + jX = Z*еjφ (1), где
X = XL - XC – реактивное сопротивление цепи,
R - активное сопротивление цепи,
Φ = arctg X/R – угол сдвига между током I и напряжением U (рис.2),
Z - полное сопротивление цепи,
ω - угловая частота.
Режим электрической цепи с последовательным соединением R, L и C, при котором ток I и напряжение U, приложенное к цепи, совпадают по фазе, называется резонансом напряжений (рис.3).
Полное комплексное сопротивление Z при резонансе должно быть чисто активным. Из (1) следует, что для резонансной частоты ω0 :
ω0L = 1/ω0C
или
ω0 = 1/√L*C (2)
Добиться резонанса в контуре с последовательным соединением R,L,C можно, изменяя ω, L, C.
Ток при резонансе имеет максимальное значение, т.к. сопротивление цепи минимальное и равно активному:
IР = U/Z = U/R (3)
Величина ρ = 1/ω0C = ω0L = √L/C называется характеристическим сопротивлением контура. Она равна модулю сопротивлений индуктивности или емкости на резонансной частоте.
Величина Q = Uco/U = ULO/U = 1/ ω0CR = ω0L/R = (√L/C)/R = ρ/R называется добротностью контура. Она показывает, во сколько раз напряжение на индуктивности или емкости больше, чем напряжение на входе схемы.
Рассмотрим частотно-избирательные свойства контура.
Введем понятие относительной частоты
ω* =ω/ω0, где
ω – текущая частота,
ω0 – резонансная частота.
Обобщенной расстройкой контура относительно резонансной частоты называется отношение:
ζ = (ωL-1/ωC)/R=(ω0ωL/ω0 – ω0/ω0ωC)/R = ρ/R*(ω/ω0 – ω0/ω)=Q(ω* - 1/ω*)
Найдем зависимость I = ƒ(ζ).
I = U/Z = U/R+j(ωL-1/ωC) = U/R*(1/(1+jζ) = IP(1/(1+jζ), где
Ip – резонансный ток, определяемый по соотношению (3)
Найдем отношение:
I/Ip = 1/(1+jζ) = 1/(√1+ζ2)*е-jφ(ζ)
Модуль:
I I/Ip I = 1/ (√1+ζ2) = 1/(√1+Q2(ω*+1/ω*)2
Представляет собой амплитудно-частотную характеристику контура и является уравнением резонансной кривой (рис.4). Вид резонансной кривой полностью определяется добротностью Q.
Рис.4 Рис.5
Функция φ = arctg (ζ) представляет собой фазочастотную характеристику контура (рис.5).
Зависимость I, UL, UC от частоты также называются резонансными кривыми (рис.6).
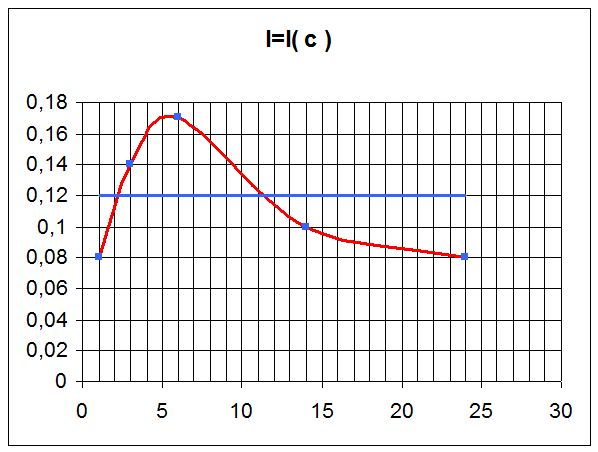
Для характеристики избирательных свойств контура вводят условное понятие полосы пропускания. Принято условно говорить, что цепь пропускания частоты, для которых I≥Ip / √2, т.е. когда мощность I2R , выделяемая на сопротивление R при частоте ω, больше половины мощности I2pR при резонансе.
Точки пересечения линии Ip /2 с резонансной кривой позволяют определить полосу пропускания, ограниченную частотами ω1 и ω2 (рис.6).
Рис.6 Рис.7
Используя частоты ω1 и ω2 можно определить добротность контура:
Q = 1/(ω2/ω0 – ω1/ω0) = ω0/(ω2 – ω1), где
ω0 = √ω1ω2 – резонансная частота.
Кривые, выражающие зависимости величин I, UL , UC от индуктивности или емкости называются настроечными характеристиками (рис.7). По настроечной емкости С1 и С2 , соответствующие точкам пересечения линии Ip / √2 с кривой I(C)
Ip /√2 = U/R√2 = U/(√R2+(ωL-1/ωC2)
Решая полученное уравнение относительно С, получим:
С1 = 1/(ω2L-ωR); C2 = 1/(ω2L+ωR). (4)
Тогда, с учетом (4), находим параметры R и L
R = 1/2ω(1/C1 – 1/C2), (5)
L = 1/2ω2(1/C1 + 1/C2). (6)
Добротность контура определяется из соотношений (5,6)
Q = ωL/R = (C1+C2) / (C1 – C2).
Техника эксперимента: Лабораторная установка смонтирована на специальном стенде, на лицевой панели которого размещены элементы исследуемой схемы:
Резистора с заданным активным сопротивлением R, катушки с индуктивностью L и активным сопротивлением rk , батареи статических конденсаторов, емкость которой можно изменять тумблерами B в пределах от 0 до 34,75 мкФ.
В качестве источника используется генератор звуковой частоты Г3-34.
Измерение напряжения осуществляется с помощью вольтметра с пределом измерения 0-75 В, классом точности 0,5.
Исследуемая электрическая цепь собирается в соответствии со схемой на рис.8
Рис.8
Напряжение на исследуемую цепь подается с генератора Г3-34 в диапазоне 5–10 В и устанавливается ручкой плавной регулировки выхода генератора.
Порядок выполнения работы:
Задание 1:
1. Собрать схему, изображенную на рис.8. Установить с помощью генератора частоту сети f=fЗАД и напряжение на входе схемы в пределах 5…10 В.
2. Изменяя величину емкости С батареи конденсаторов, получить резонанс напряжений, т.е. добиться, чтобы в цепи протекал максимальный ток. При максимальном токе напряжение на резисторе будет максимальным, поэтому резонанс напряжений фиксируется по вольтметру UR. Записать показания приборов в таблицу 1.
3. Произвести измерения при емкости батареи конденсаторов меньшей, чем при резонансе и измерения при емкости батареи, больше резонансной. Записать показания приборов в таблицу 1.
R= 10 Ом, f= 300 Гц.
Таблица 1.
|
Номер п/п |
Данные измерения |
Данные расчета |
|||
|
C,мкФ |
UR, В |
UK, В |
UC, В |
I=UR/R, А |
|
|
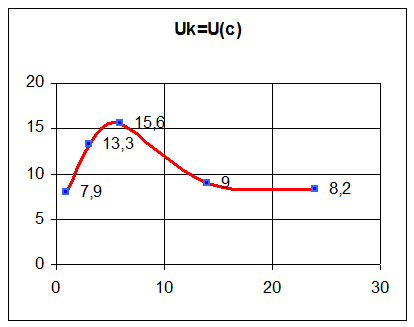
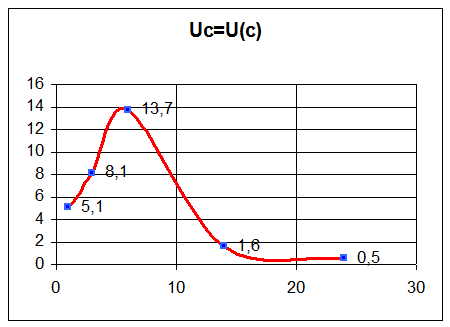
1 |
6 |
1,7 |
15,6 |
13,7 |
0,17 |
|
2 |
3 |
1,4 |
13,3 |
15,1 |
0,14 |
|
3 |
1 |
0,8 |
7,9 |
7,9 |
0,08 |
|
4 |
14 |
1 |
9 |
1,6 |
0,1 |
|
5 |
24 |
0,8 |
8,2 |
0,5 |
0,08 |
Задание 2:
1. Установить емкость батареи конденсаторов, установить напряжение на входе схемы в пределах 5…10 В.
2. Изменяя частоту, получить резонанс напряжений, фиксируя момент резонанса по вольтметру UR. Записать показания приборов в таблицу 2.
3. Произвести измерения при частотах, меньших резонансной, и, измерения при частоте, большей резонансной. Результаты записать в таблицу 2.
С= 6 мкФ, R= 10 Ом.
Таблица 2.
|
Номер п/п |
Данные измерения |
Данные расчета |
|||
|
f, Гц |
UR, В |
UK, В |
UC, В |
I= UR/R, А |
|
|
1 |
300 |
1,7 |
15,6 |
13,7 |
0,17 |
|
2 |
200 |
0,7 |
12,1 |
10,5 |
0,07 |
|
3 |
100 |
0,31 |
3,4 |
7,9 |
0,031 |
|
4 |
400 |
0,8 |
9,2 |
1,8 |
0,08 |
|
5 |
500 |
0,6 |
8,7 |
1,1 |
0,06 |
Обработка результатов эксперимента:
Построим кривые зависимостей I=I(c), Uk=U(c), Uc=U(c), Ul=U(c)
 |
 |
Для построения графика
зависимости Ul=U( c ) необходимо рассчитать активное сопротивление катушки rk. Для этого на графике I=I( c )
проводим линию ![]() .
.
 |
![]() [Ф]
[Ф]
![]() [Ф]
[Ф]
Активное сопротивление цепи:
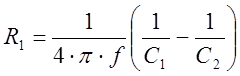
![]() [Ом]
[Ом]
![]() [Ом]
[Ом]
Тогда величину Ul для каждого значения емкости можно найти по формуле:
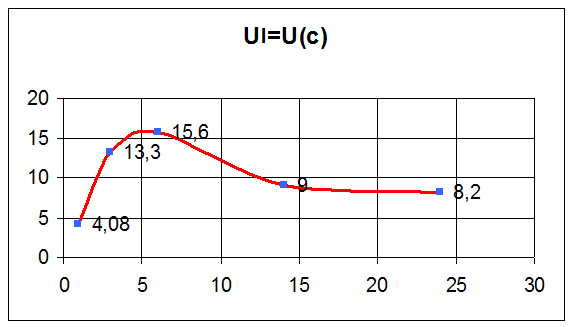
![]()
|
С, мкФ |
Ul, В |
|
1 |
4,08 |
|
3 |
13,3 |
|
6 |
15,6 |
|
14 |
9 |
|
24 |
8,2 |
Индуктивность катушки Lk :
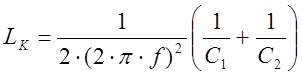
![]() [Гн]
[Гн]
Добротность контура находится по формуле:
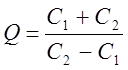
![]()
Характеристическое сопротивление
контура: ![]() ρ=143,18 [Ом]
ρ=143,18 [Ом]
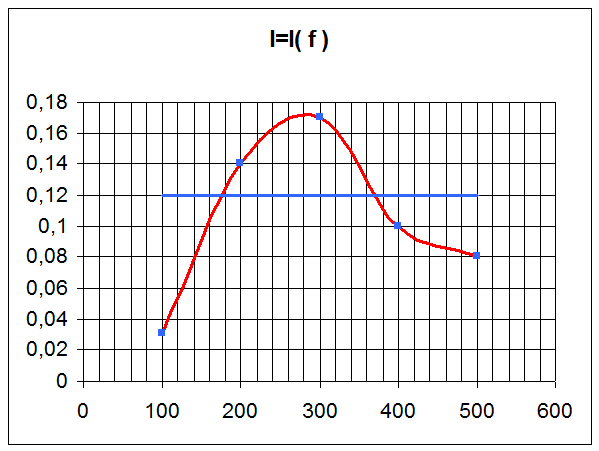
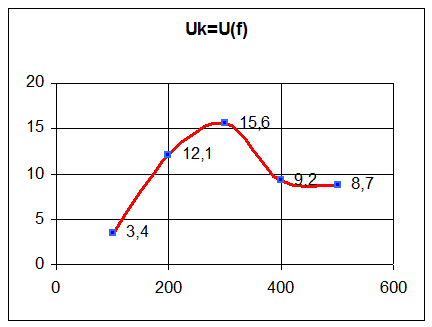
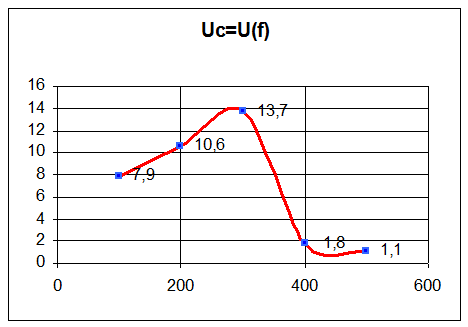
Построим графики зависимостей I=I(f), Uc=U(f), Uk=U(f).
 |
|||||
 |
 |
||||
Ширина полосы пропускания: ![]() [рад/с]
[рад/с]
Рассчитаем по графику I=I(f) добротность контура:
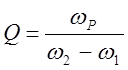
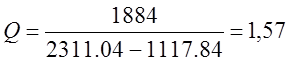
Сравнив экспериментально найденное значение добротности контура с рассчитанным по формуле, можно сделать вывод, что значение добротности конура является достоверным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.