МИНИСТЕРСТВО ОБЩЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
КАФЕДРА СММ
САМОСТОЯТЕЛЬНАЯ РАБОТА №2
ВАРИАНТ №42
Выполнил ст. гр. УИТ-22
Балаково 2004
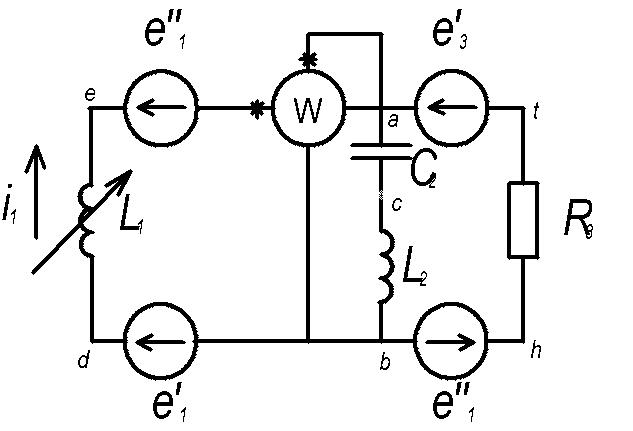
L1=21.2 мГн
L2=39.8 мГн
C2=75.6 мкФ
R3=25 Ом
f=60 Гц
e’1=70.5 cos(wt-90 ̊) B
e’’1=0 B
e’3=84.6 sin(wt+330 ̊) B
e’’3=0 B
Решение.
0. Подготовка исходных данных.
w=2πf=2*3.14*60=376.8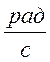 
e’1=70.5 cos(wt-90̊)=70.5 sin(wt-90̊+90̊)=70.5 sin wt В
E1’=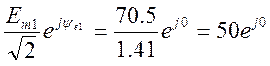
B=50 B
E3’=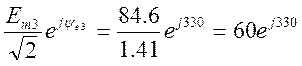
B=60(cos 330̊+j sin 330̊)=52-30j
B
XL1=wL1=376.8*21.2*10-3=8 Ом
XL2=wL2=376,8*39,8*10-3=15 Ом
Xc2=
=
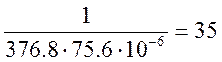Ом
e’’1, e’’3 можно исключить (ЭДС равны нулю).
1. Уравнения на основании законов Кирхгофа.
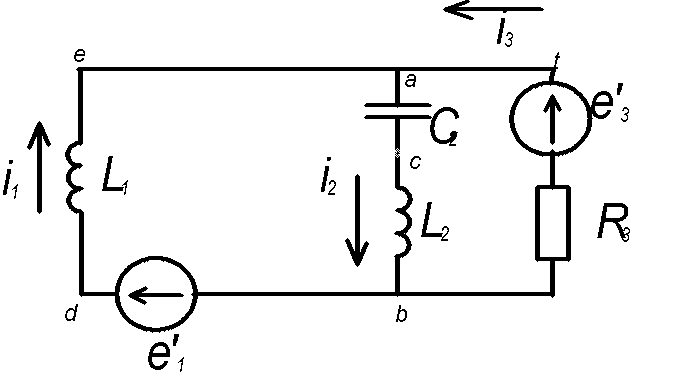
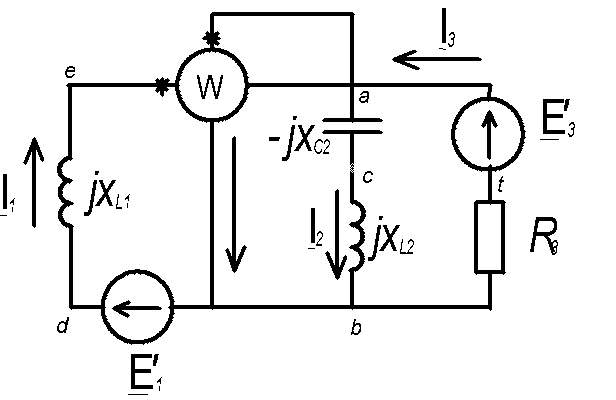
а) Составим систему уравнений в дифференциальной форме, для этого перерисуем схему без ваттметра, покажем токи в мгновенных значениях. (рисунок см. ниже)
Первый закон Кирхгофа для узла А:
i1-i2+i3=0
 |
 |
||
Второй закон для двух контуров в дифференциальной форме:
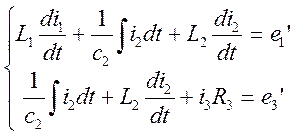
б) Составим систему уравнений в комплексной форме. Для этого перечертим схему:
|
||||||
 |
||||||
 |
||||||
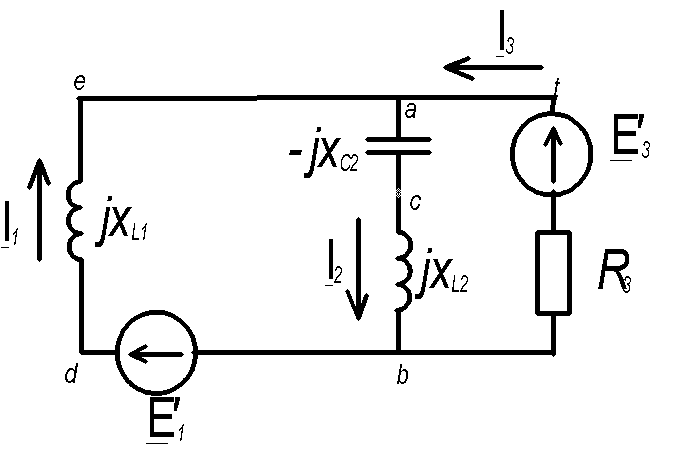
1) Для узла А: I1-I2+I3=0
2) I1 jxL1-I2 jxC2 +I2 jxL2=E1
I3 R3-I2 jxC2 +I2 jxL2=E3
2. Определение комплексов действующих значений токов.
Рассчитаем токи по МКТ, для этого решим систему:
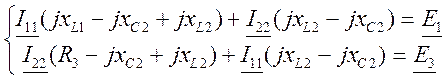
Решим систему матричным способом с помощью программы MathCad:
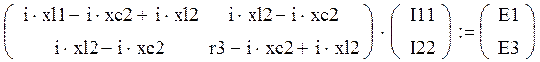
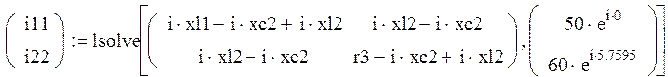, где 5.7595=330̊
Получили результат:
I11=2.429+4.828jA = I1
I22= -1.464-0.424j A = I3
I2=I11+I22
I2=0.965+4.405j A
3.Определение показаний ваттметра.
 |
|||||
|
|||||
|
|||||
Мощность на ваттметре находится по формуле:
а) P=Re[Uab·I1*
] (
в MathCad)
Uab находим из контура abca: Uab-I2(jxL2-jxC2)=0; Uab=I2(jxL2-jxC2)
В MathCad
находится по формуле: 
, получим:
Uab=88.57-19.407j B
I1*= 2.429-4.828j A
P= 121.473 Вт
 |
б)P=UI cos φ P=UabI1cos(UabI1)
Для определения разности фаз φ между током и напряжением построим векторную диаграмму:
масштаб тока: mI=1
(I1= 2.429+4.828j A)
масштаб напряжения: mU=10
(Uab=88.57-19.407j B)
|
||||
|
||||
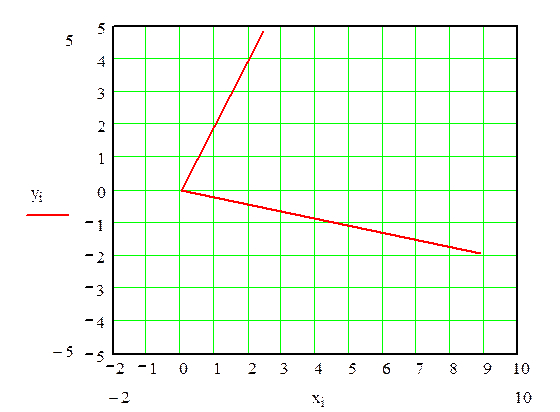
Из графика получим:
I1=5.2 A
|
Uab=9.2*10=92 B
|
|
P=5.2*92*cos 75̊=123.8 Вт
Мощности, найденные обеими методам, оказались приблизительно равными.
4. Построение топографической диаграммы напряжений, совмещенной с векторной диаграммой токов.
Потенциал узла а примем равным нулю: φа=0 В
Найдем значения потенциалов в точках контура afbdea:
φf=φa-E3=0-52+30j=-52+30j B
φb=φf+I3R3=-52+30j+(-1.464-0.424j)*25=-88+19j B
φd=φb+E1=-88+19j +50=-38+19j B
φe=φa=φd-I1jxL1=-38+19j-(2.429+4.828j)*j*8=-38+19j-19j+38=0 B
φc=φa-I2jxc2=-(0.965+4.405j)*j*35=154-34j В (на рисунке не показано)
масштаб тока: mI=1 
масштаб напряжения: mU=10
|
|
|
|
|
|
|
|
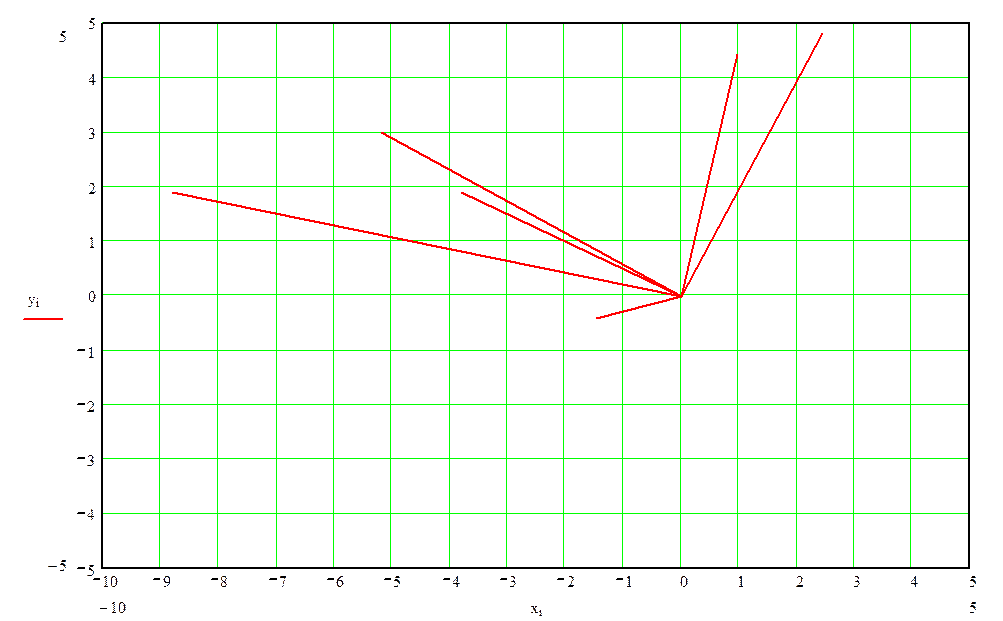
5. Построение круговой диаграммы тока.
Воспользуемся методом эквивалентного генератора:
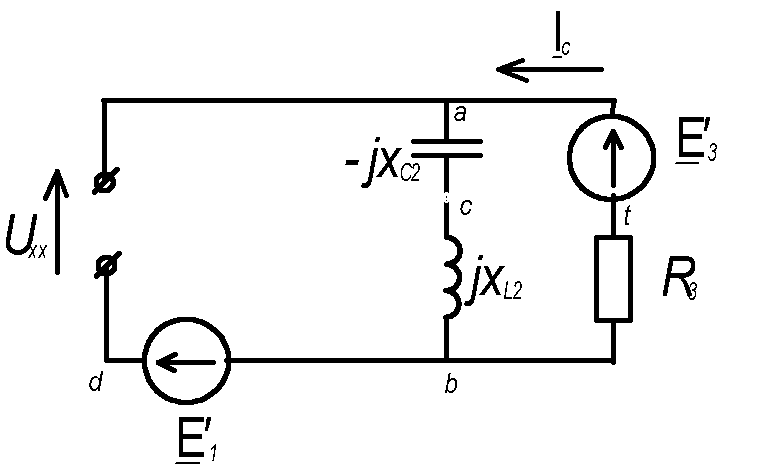
По второму закону Кирхгофа для контура acbfa: Ic(jxL2-jxc2+R3)=E3
Ic=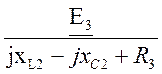
= 1.848+0.286i А,
для контура dafbd: Uxx-IcR3=E1-E3; Uxx=E1-E3+IcR3= 44.24+37.161i В –напряжение холостого хода
zBX=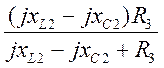
= 9.82- 12.209i=15.7ej(-51̊) Ом – входное
сопротивление
zBX=15.7 φBX=-51̊
Iкз=
= -0.078+3.687i
A – ток короткого замыкания
сдвиг фаз нагрузки: φн=90̊ - нагрузкой является катушка.
полный сдвиг фаз: ψ= φн -φBX=90 ̊̊̊-(-51̊)=141̊
масштаб по току mI=1 масштаб
сопротивления: mR=5
6. График изменения тока в изменяющемся сопротивлении в зависимости от модуля этого сопротивления. (Находится из круговой диаграммы)
7. Нахождение мгновенного значения тока i1.
Из пункта 2: I1=2.429+4.828j A =5.405еj63.29̊
I1=5.405 A, I1m=5.405
=7.644 A, ψ=63.29̊
(при t=0).
Из полученных данных следует:
i1= I1msin(wt+ ψ)= 7.644 sin(wt+63.29̊) A
Получаем график:
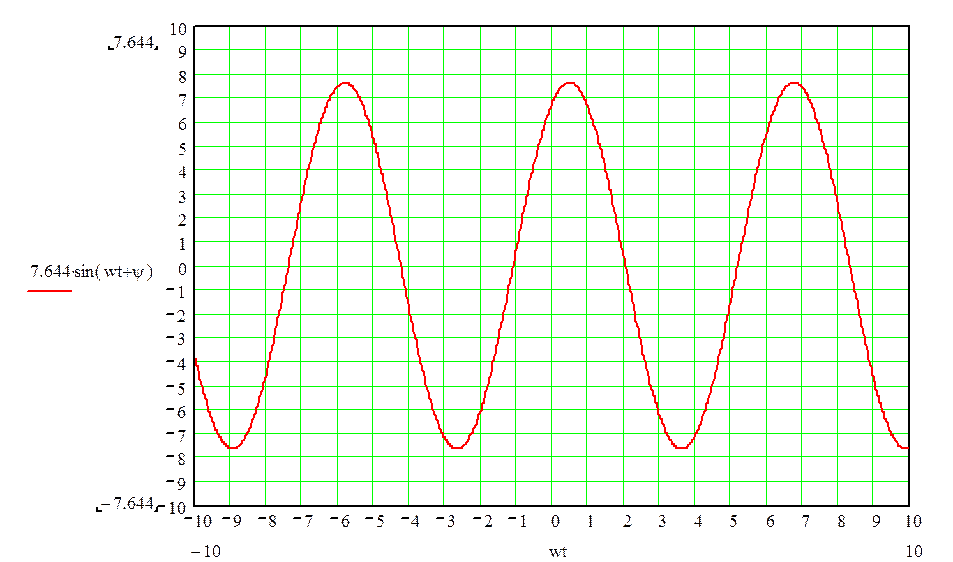
8. Магнитная связь между катушками.
Покажем встречную включение катушек и их магнитную связь:
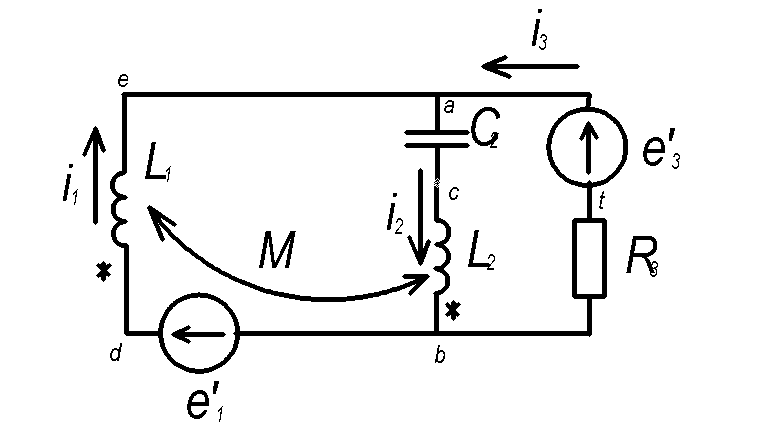
а) Запись законов Кирхгофа в дифференциальной форме:
i1-i2+i3=0
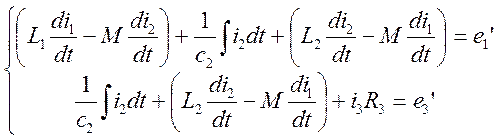
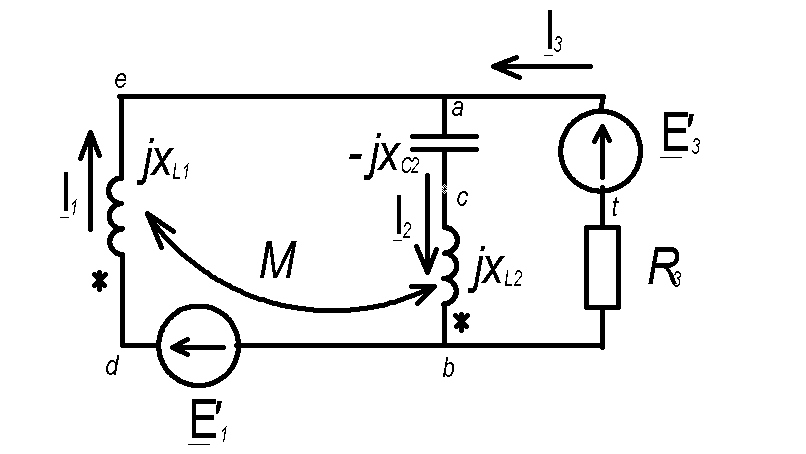
б) Запись законов Кирхгофа в комплексной форме:
1) Для узла А: I1-I2+I3=0
2) (I1 jxL1-I2 jxM)-I2 jxC2 +(I2 jxL2- I1 jxM)=E1
I3 R3-I2 jxC2 +(I2 jxL2- I1 jxM)=E3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
