Лабораторная работа № 2.
Исследование резонанса напряжения.
Цель работы: экспериментальное исследование цепи синусоидального тока с последовательным соединением элементов, определение условий, при которых наступает резонанс, определение параметров в схеме резонансным методом.
Техника эксперимента.
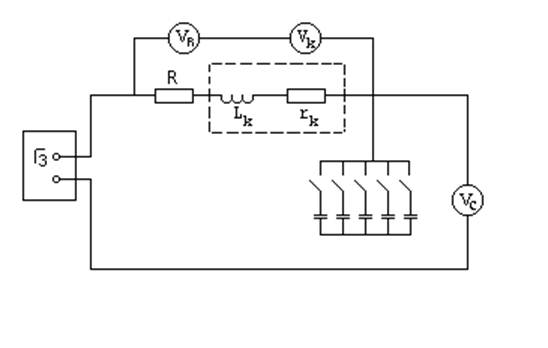
Лабораторная установка смонтирована на специальном стенде, на лицевой панели, которого размещены элементы исследуемой схемы: реостат заданным активным сопротивлением R, катушки с индуктивностью L и активным сопротивлением rn, батарея статистических конденсаторов, емкость которую можно изменять тумблером в пределах от 0 до 34,75 мкТ. В качестве источника используется генератор звуковой частоты Г3-34. Измерение напряжения осуществляется с помощью вольтметра с пределом измерения 0-75 В, классом точности 0,5. Напряжение на исследуемою цепь подается с генератора Г3-34 в диапазоне 5-10 В и устанавливается ручкой плавной регулировки выхода генератора.
|
Номер опыта |
данные измерений |
Данные расчётов |
|||
|
С,мкФ |
UR,B |
UK,B |
UC,B |
I=UR/R, A |
|
|
1 |
0,0000015 |
1,25 |
28 |
27 |
0,083 |
|
2 |
0,0000005 |
0,275 |
5 |
17 |
0,018 |
|
3 |
0,000001 |
0,75 |
16 |
25 |
0,050 |
|
4 |
0,000002 |
1 |
23 |
15 |
0,067 |
|
5 |
0,0000025 |
0,9 |
20 |
11 |
0,060 |
Строим кривые I(c), Uk(c), Uc(c), Ul(c).

По характеристике I(c) определим активное сопротивление R + rk и величину индуктивности Lk по формулам R=(1/2w)((1/C1)-(1/C2)) и Lk=(1/2w2)((1/C1)+(1/C2)). Найдем полосу пропускания. Для этого проведем на графике I=I(c) прямую Iр/Ö2 и найдем C1 и C2 по пересечению ее с кривой.
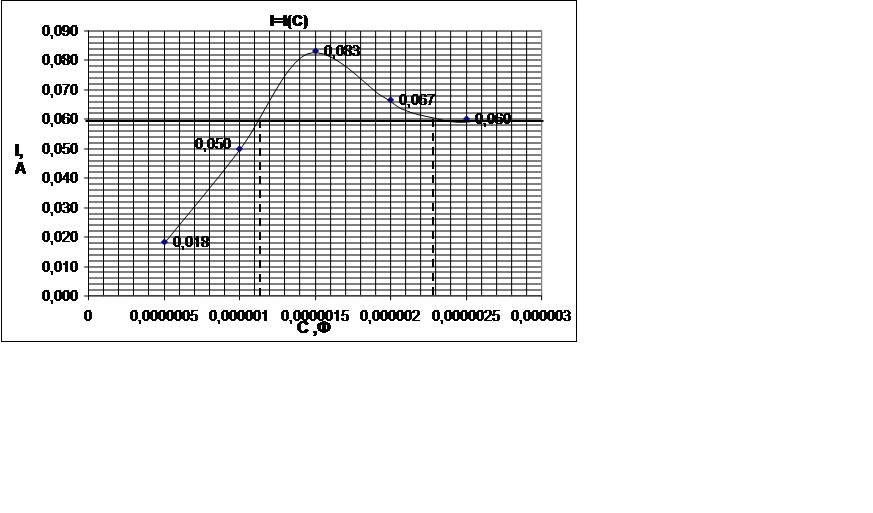
С1=1.11
10-6
По условию, что f=340 Гц, то w=2pf
w=2136,3 рад с-1
Получим
R=(1/2*213,3)((1/1.11 10-6)-(2.5 10-6))=117,3 Ом
Отсюда
rk=R-R1, R1=15 Ом
Из условий опыта следует, что rk=117,23-15=102,23 Ом
L=(1/2*213,3)((1/1.11 10-6)+(2.5 10-6))=0,14 Гн
Определим добротность контура по формуле Q=wL/R=(C1+C2)/(C2-C1)=3
Найдем напряжение Ul для каждого значения электроемкости по формуле Ul=Ö(Uk2-(Irk)2)
1) C=1,5 мкФ, Ul=26,68
2) C=0,5 мкФ, Ul=4,65
3) C=1 мкФ, Ul=15,16
4) C=2 мкФ, Ul=21,96
5) C=2,5 мкФ, Ul=19
Найдем характеристическое сопротивление контура по формуле r=QR
r=351,69
1) для случая C=C0, IR=9,73 В
2) для случая C<C0
IR=5,8615
IjXl=IjwL=14,95
IjXc=Ij/wC=23,4
Z=R+jXl-jXc=117,23-169j
3) для случая C>C0
IR=7,85 В
IjXl=IjwL=20 В
IjXc=Ij/wC=15,68 В
Z=R+jXl-jXc=117,23+65,03j Ом
4) по таблице 2 посроим кривые I(f),Uc(f),UR(f) по кривой I(f), определим ширину пропускания, для этого проведем полосу IR/Ö2, то есть IR/Ö2=0,059 А. Получим f1=250 Гц, f2=425 Гц. Тогда
w1=2pf1=1517 rad s-1
w2=2pf2=2670 rad s-1
тогда полоса пропускания Dw=w2-w1=1099 рад с-1
рассчитаем добротность контура по формуле
Q=wL/R=2pf0L/R
Q=2,85
Рассчитаем погрешность:
DQ=eQ=(eС1+eС2)Q=
Как видим, все ништяк
Вывод: в ходе выполнения лабораторной работы мы на практике познакомились с понятием «резонанс напряжений» (состоянием электрической цепи, при котором напряжение и ток в ней совпадают по фазе), и с условиями его возникновения (линейная электрическая цепь, состоящая из последовательно соединенных резистивного, индуктивного и емкостного элементов, полное электрическое сопротивление которой имеет чисто активный характер на заданной частоте, то есть Z = R + jXL – jXC = R, jXL – jXC = 0, jXL = jXC, где XL = wL, XC = 1/wC). Мы выяснили, что при резонансе ток в цепи принимает максимальное значение, поскольку в этом случае сопротивление цепи минимально и равно активному. Также мы убедились в том, что резонанс напряжений возникает при определенной частоте w0, называемой резонансной, зависящей от параметров схемы. Мы определили, что при отклонении частоты от резонансной и на резонансной частоте при изменении параметров схемы (в нашем случае C), цепь выходит из состояния резонанса (значение тока уменьшается). Следовательно, данная цепь обладает частотной избирательностью (селективностью).
В ходе работы мы исследовали частотно-избирательные свойства контура, состоящего из последовательно соединенных катушки, конденсатора и резистора, определили его основные параметры – характеристическое сопротивление (реактивное сопротивление индуктивности или емкости на резонансной частоте, r = w0L = 1/w0C = (L/C)1/2), добротность (отношение напряжения на емкости или индуктивности к входному, Q = UC,L/U = r/R) и полосу пропускания (диапазон частот, симметричный относительно резонансной частоты, для которого выделяемая на активном сопротивлении мощность превышает половину мощности при резонансе, w0 ± w0/2Q), и построили резонансные кривые, настроечные характеристики, и векторные диаграммы. Полученные экспериментальные данные мы сравнили с расчетными (теоретическими), и убедились в их равенстве (с учетом погрешностей).
На основании этого можно сделать вывод, что цель работы нами достигнута полностью.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.