9.1. Аналитический способ определения параметров периодического движения
САУ позволяет определить ![]() и
и
![]() из системы управлений:
из системы управлений:
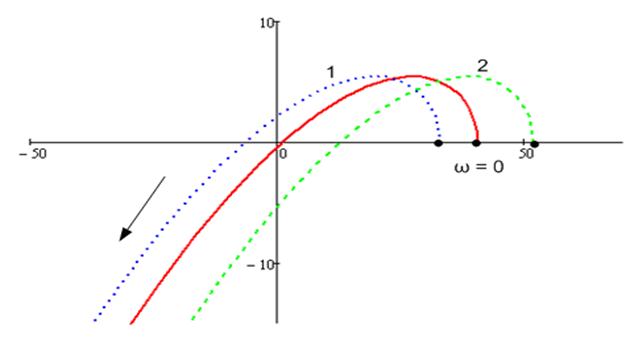
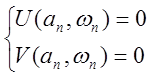 (*)
(*)
где ![]() ,
, ![]() вещественная и мнимая составляющие
кривой Михайлова:
вещественная и мнимая составляющие
кривой Михайлова: ![]()
Если решение системы (*) существует(![]() - вещественные положительные числа),
то, давая приращение амплитуде
- вещественные положительные числа),
то, давая приращение амплитуде ![]() , оценивается
устойчивость системы. Для найденного периодического решения
, оценивается
устойчивость системы. Для найденного периодического решения ![]() кривая Михайлова
кривая Михайлова ![]() проходит через начало координат
.Если для положительных приращений амплитуды
проходит через начало координат
.Если для положительных приращений амплитуды ![]() ,
кривая Михайлова займет положение (1), а для отрицательных
,
кривая Михайлова займет положение (1), а для отрицательных ![]() - положение (2), то найденное решение
устойчивое и нелинейная САУ устойчива в «большом».В противном случае найденное
решение неустойчивое, система устойчива в малом.
- положение (2), то найденное решение
устойчивое и нелинейная САУ устойчива в «большом».В противном случае найденное
решение неустойчивое, система устойчива в малом.
9.2. Виды модуляции в импульсных системах
Импульсной называется система, содержащая по крайней мере один импульсный элемент.
На вход импульсного элемента, осуществляющего квантование, подается непрерывный сигнал, а на его выходе формируется последовательность импульсов, форма которых может быть самой разнообразной. Она зависит от вида модуляции, реализуемой в импульсном элементе. Параметры импульсов изменяются в соответствии со значением входного сигнала и этот процесс их изменения и называется модуляцией.
Различают следующие виды модуляции:
1. Амплитудно-импульсная модуляция (АИМ)
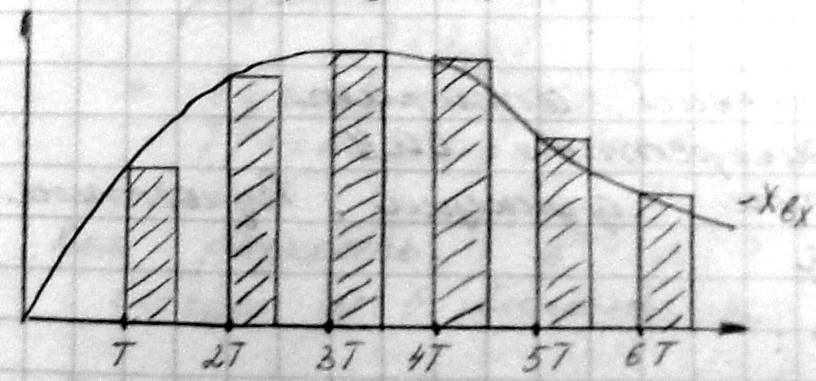
Между импульсами одинаковые расстояния. Ширина импульсов тоже постоянна. Меняется амплитуда импульсов.
2. Широтно-импульсная модуляция (ШИМ)
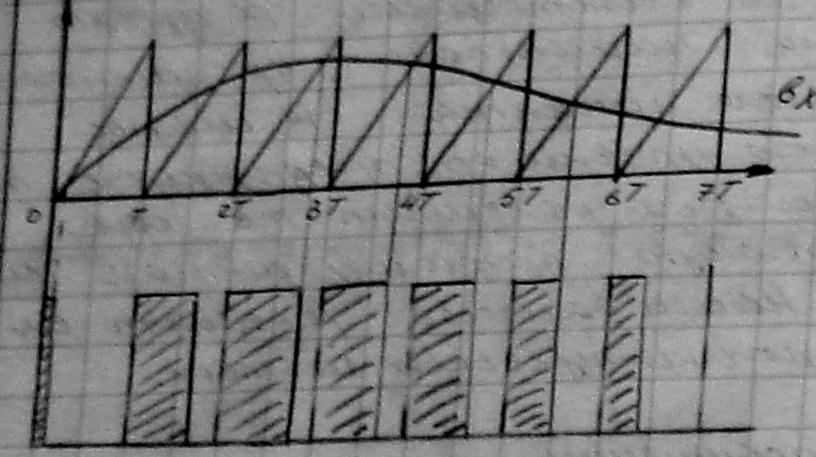
При этом виде модуляции амплитуда импульсов постоянна, а меняется только ширина импульсов.
3. Частотно-импульсная модуляция (ЧИМ)
4. Время-импульсная (или фазо-импульсная) модуляция (ФИМ)
При АИМ структурную схему системы можно представить :
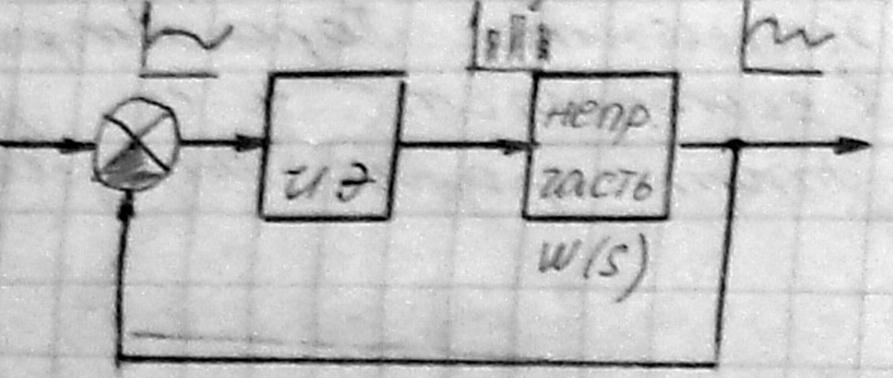
ИЭ – импульсный элемент
Параметры:
![]() - Период квантования
- Период квантования
![]() Коэффициент усиления по
амплитуде
Коэффициент усиления по
амплитуде
![]() Длительность импульса
Длительность импульса
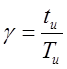 Относительная длительность
импульса
Относительная длительность
импульса
10.1. Графический способ определения параметров периодического движения
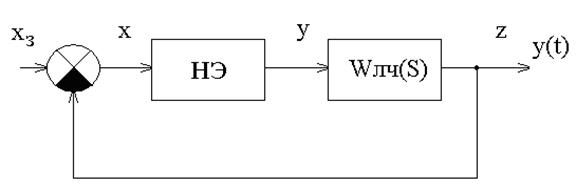
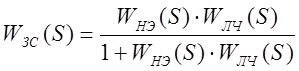
![]() -передаточная функция линейной части
НСАУ;
-передаточная функция линейной части
НСАУ;
![]() -комплексный коэффициент передачи гармонически
линеаризованного нелинейного элемента
-комплексный коэффициент передачи гармонически
линеаризованного нелинейного элемента
Характеристическое уравнение ![]()
Граница устойчивости ![]()
![]()
![]()
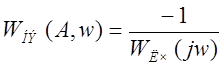
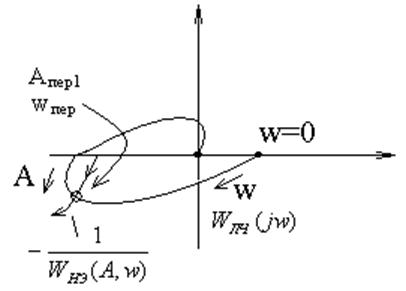 На комплексной плоскости в одном масштабе строится
годографы:
На комплексной плоскости в одном масштабе строится
годографы: ![]() и
и 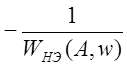
Если эти годографы пересекаются, то точка их
пересечения определяется амплитуду и частоту периодических колебаний. По
характеристике 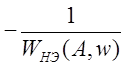 определяют амплитуду
колебаний
определяют амплитуду
колебаний ![]() , а по годографу
, а по годографу ![]() – частоту
– частоту ![]() .
Для оценки устойчивости найденного периодического движения необходимо дать
приращение амплитуде.
.
Для оценки устойчивости найденного периодического движения необходимо дать
приращение амплитуде.
Если А=Апер+а модуль годографа 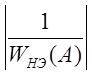 возрастает по сравнению с модулем
возрастает по сравнению с модулем 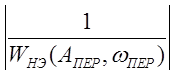 , а при А=Апер-а модуль
годографа
, а при А=Апер-а модуль
годографа 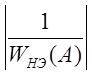 уменьшается по сравнению с модулем
уменьшается по сравнению с модулем 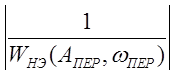 , то периодическое движение абсолютно
устойчиво(«в большом») и соответствует автоколебаниям.
, то периодическое движение абсолютно
устойчиво(«в большом») и соответствует автоколебаниям.
Если при увеличении амплитуды А годограф 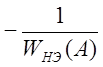 пересекает частотную характеристику
АФЧХ ЛЧ из внутренней её области во внешнюю, то периодическое движение
абсолютно устойчиво(«в большом») и соответствует автоколебаниям.
пересекает частотную характеристику
АФЧХ ЛЧ из внутренней её области во внешнюю, то периодическое движение
абсолютно устойчиво(«в большом») и соответствует автоколебаниям.
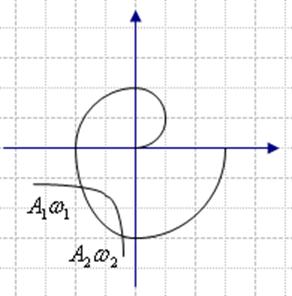 Если пересечений
годографов линейной и нелинейной частей нет, то в системе отсутствует
периодическое движение.
Если пересечений
годографов линейной и нелинейной частей нет, то в системе отсутствует
периодическое движение.
При графическом определении параметров автоколебаний возможно несколько решений
10.2. Виды квантования в импульсных системах
В зависимости от способов передачи и преобразования сигналов системы автоматического управления можно разделить на:
- непрерывные САУ (В непрерывных системах сигналы в процессе преобразования не прерываются)
- дискретные САУ (В дискретных системах имеются элементы или звенья, превращающие непрерывные сигналы в последовательность импульсов или в ряд квантованных сигналов, или в цифровой код).
Различают 3 вида квантования и, соответственно, 3 класса дискретных САУ:
1. Релейные системы. Квантование по уровню.
 Системы в которых присутствует квантование по уровню и отсутствуют
другие виды квантования.
Системы в которых присутствует квантование по уровню и отсутствуют
другие виды квантования.
Происходит фиксация дискретных уровней сигнала в определённые моменты времени. Для квантования по уровню используется многопозиционный релейный элемент
Характеристика релейного элемента
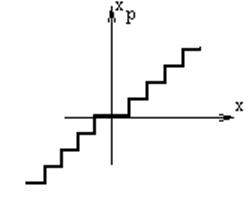
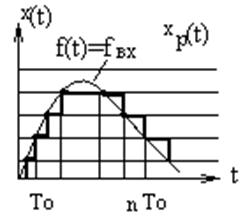 Результаты
квантования по уровню, Хр - квантованный сигнал.
Результаты
квантования по уровню, Хр - квантованный сигнал.
Так как в качестве квантователя непрерывного сигнала Х(t) используется релейный элемент, то дискретные САУ называются релейными. Такой класс дискретных относят к классу нелинейных систем, а для анализа и синтеза релейных систем используют теорию нелинейных систем. При увеличении числа уровней и малом отличии соседних уровней релейную систему можно рассматривать как релейную непрерывную.
2.
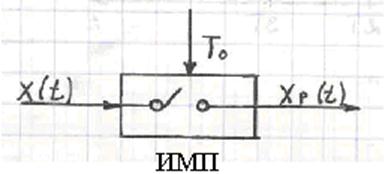 Импульсные системы. Квантование по времени.
Импульсные системы. Квантование по времени.
Системы в которых присутствует квантование по времени и отсутствуют другие виды квантования.
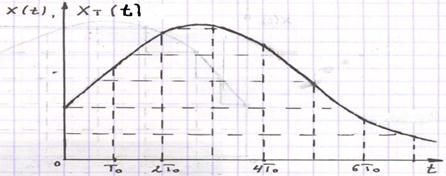
Происходит фиксация непрерывного сигнала в дискретные моменты времени : 0, T, 2T, 3T и т.д. Квантование непрерывного сигнала можно получить, пропуская непрерывный сигнал через ключ, который периодически с тактом квантования Т замыкается на время h. В дискретных САУ этот элемент называют импульсным элементом .
3. Релейно-импульсные системы (цифровые). Квантование по уровню и времени.
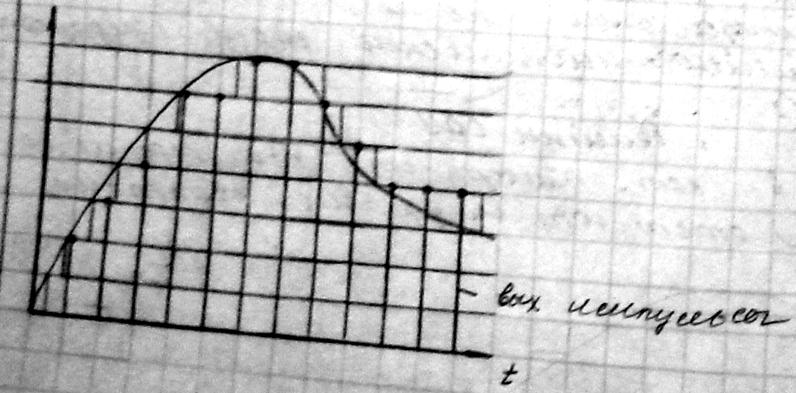 Системы, в которых одновременно присутствует квантование
по уровню и квантование по времени.
Системы, в которых одновременно присутствует квантование
по уровню и квантование по времени.
В дискретные моменты времени : 0, T, 2T, 3T и т.д. выбираются значения непрерывной функции Х(t) и в дальнейшем они фиксируются на ближайшем уровне.
11.1. Критерий абсолютной устойчивости Попова
Этот критерий применяется для исследования устойчивости НСАУ с одним нелинейным элементом и устойчивой линейной частью.
Этот критерий является устойчивым.
Критерий достаточный: если он выполняется то система устойчива, если не выполняется, то система может быть как устойчивой, так и неустойчивой.
Для применения этого критерия систему необходимо привести к следующему виду:
|
При однозначной нелинейной характеристике: |
При неоднозначной нелинейной характеристике: |
|
|
|
 Формулировка:
для того чтобы положение равновесия нелинейной системы с устойчивой линейной
частью и однозначной нелинейностью было устойчиво необходимо и достаточно
выполнение следующих условий:
Формулировка:
для того чтобы положение равновесия нелинейной системы с устойчивой линейной
частью и однозначной нелинейностью было устойчиво необходимо и достаточно
выполнение следующих условий:
1.
Действительная часть функции Попова должна быть больше нуля 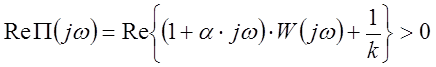
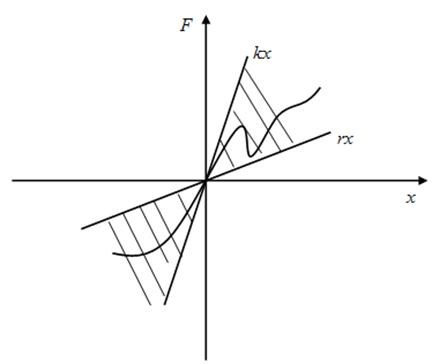
2. Нелинейная
характеристика должна удовлетворять условию 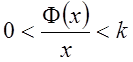
1. Абсолютная устойчивость проверяется при любых начальных условиях.
2.
Абсолютная устойчивость имеет месть при любой нелинейности внутри
сектора ![]()
Рассмотрим первое условие о функции Попова:
![]() ,
,![]() -
действительные числа;
-
действительные числа; ![]() - связывает оба условия
критерия.
- связывает оба условия
критерия.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.